Hinweise der Studienberater
Orientierungsprüfung
Vordiplom, Zwischenprüfung
Sprechstunden
Arbeitsgebiete
1 Vorlesungen
1.1 Elementare Differentialgeometrie
1.2 Partielle Differentialgleichungen
1.3 Elementare Zahlentheorie
1.4 Funktionentheorie
1.5 Mathematische Logik
1.6 Wahrscheinlichkeitstheorie
1.7 Numerik II
1.8 Differentialgeometrie II
1.9 Theorie und Numerik partieller Differentialgleichungen II
1.10 Nichtstandardanalysis
1.11 Stochastik für Studierende der Informatik
1.12 Kontrolltheorie und Optimale Steuerung
1.13 Modelltheorie und algebraische Geometrie
1.14 Stochastische Prozesse und Finanzmathematik
1.15 Nichtlineare Funktionalanalysis
1.16 Didaktik der Algebra und Analysis
1.17 Ricci-Krümmung auf metrischen Räumen
1.18 Schemes and Zeta functions
2 Praktika
2.1 Grundlagen der Programmiersprache C für Studierende der Naturwissenschaften
2.2 Statistisches Praktikum
2.3 Statistische Verfahren in R
2.4 Numerik II
2.5 Numerik partieller Differentialgleichungen auf Mannigfaltigkeiten
3 Proseminare
3.1 Das Buch der Beweise
3.2 Mathematik im Alltag
3.3 Algebra
3.4 Modellierung
3.5 Große Sätze und schöne Beweise
3.6 Fourieranalysis
4 Seminare
4.1 Differentialgeometrie von Kurven und Flächen
4.2 Algebraische Topologie
4.3 Geometrische Analysis
4.4 Metrische Räume mit Schnittkrümmung ≥ k
4.5 Seminar über
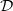-Moduln
4.6 Zahlentheorie
4.7 Modelltheorie
4.8 Finanzmathematik
4.9 Verzweigungsprozesse
4.10 Statistische Modelle in der klinischen Epidemiologie
4.11 Partielle Differentialgleichungen auf Flächen
4.12 Medieneinsatz im Mathematikunterricht
4.13 Einsatz unterschiedlicher Unterrichtsmethoden
4.14 Concepts Maps als Werkzeuge zur Wissensstrukturierung: Theorien, Anforderungen, Anwendungen
4.15 Embodying – Anwendungen eines transdisziplinären Konzeptes in der Geschlechterforschung
4.16 Feministische Epistemologien und ihre Anwendungen in transdisziplinären Gender Studies
4.17 Optimierung, Optimale Steuerung und Anwendungen in der Systembiologie
5 Oberseminare und Arbeitsgemeinschaften
5.1 Differentialgeometrie
5.2 Modelltheorie
5.3 Medizinische Statistik
5.4 Angewandte Mathematik
5.5 Geometrische Analysis
5.6 Algebra
5.7 Nicht-Newtonsche Flüssigkeiten
5.8 Finite Elemente
5.9 Forschungsprojekte – DoktorandInnenseminar
6 Kolloquia
6.1 Kolloquium