1.18 Schemes and Zeta functions

Inhalt:

This course has two aims: to introduce the language and some of the theory of schemes; to give an interesting arithmetic application of schemes. More specifically, we intend to study problems related to varieties over finite fields and the number of rational points they can have. This information is conveniently encoded in the zeta function of such a variety. Using the language of schemes, it is also possible to talk about a family of varieties over a family of finite fields. For example an equation such as

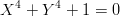
makes sense modulo every prime number p. Thus in a sense it represents a family of varieties indexed by the prime numbers. Such families give rise to schemes “of finite type over ℤ ”, and they also have zeta functions. In this course we will prove various things about such schemes, and we will see how this information is encoded in certain analytic properties of their associated zeta functions.