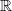 , dem üblichen “Modell der Zahlengeraden” nicht gibt. Im
19. Jahrhundert wurden diese infinitesimalen Größen durch die Präzisierung von
Grenzwertprozessen mit der ϵ-δ-Technik aus der Mathematik vertrieben.
, dem üblichen “Modell der Zahlengeraden” nicht gibt. Im
19. Jahrhundert wurden diese infinitesimalen Größen durch die Präzisierung von
Grenzwertprozessen mit der ϵ-δ-Technik aus der Mathematik vertrieben.
Vorlesung: | Nichtstandardanalysis |
Dozent: | Prof. Dr. J. Flum |
Zeit/Ort: | Mo 16–18; Mi 16–18 14-tägl., |
Übungen: | Mi 16–18 (14-tägl.), SR 119, Eckerstr. 1 |
Tutorium: | M. Müller |
Inhalt:
Beim Aufbau der Differentialrechnung arbeitete etwa Leibniz mit infinitesimalen, d.h. unendlich
kleinen Zahlen, die es in 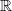 , dem üblichen “Modell der Zahlengeraden” nicht gibt. Im
19. Jahrhundert wurden diese infinitesimalen Größen durch die Präzisierung von
Grenzwertprozessen mit der ϵ-δ-Technik aus der Mathematik vertrieben.
, dem üblichen “Modell der Zahlengeraden” nicht gibt. Im
19. Jahrhundert wurden diese infinitesimalen Größen durch die Präzisierung von
Grenzwertprozessen mit der ϵ-δ-Technik aus der Mathematik vertrieben.
1960 bemerkte A. Robinson, dass der Bereich der reellen Zahlen zu einem Bereich
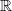 * erweitert werden kann, in dem man wie in
* erweitert werden kann, in dem man wie in 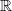 rechnen kann, der infinitesimale
Größen und unendlich große natürliche Zahlen enthält und in dem die Definitionen und
Argumentationen von Leibniz eine präzise Bedeutung erhalten. Da diese Definitionen und
Redewendungen unserer anschaulichen Vorstellung (der Begriffe der Konvergenz, Stetigkeit, …)
entsprechen, führt der Aufbau der Analysis in
rechnen kann, der infinitesimale
Größen und unendlich große natürliche Zahlen enthält und in dem die Definitionen und
Argumentationen von Leibniz eine präzise Bedeutung erhalten. Da diese Definitionen und
Redewendungen unserer anschaulichen Vorstellung (der Begriffe der Konvergenz, Stetigkeit, …)
entsprechen, führt der Aufbau der Analysis in 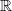 * zu einem tieferen Verständnis und ist
zugleich (etwa für Lehrer/Lehrerinnen) eine Quelle für anschauliche, aber präzisierbare
Formulierungen und Argumentationen. “Non-standard analysis frequently simplifies
substantially the proofs, not only of elementary theorems, but also of deep results” (Kurt
Gödel).
* zu einem tieferen Verständnis und ist
zugleich (etwa für Lehrer/Lehrerinnen) eine Quelle für anschauliche, aber präzisierbare
Formulierungen und Argumentationen. “Non-standard analysis frequently simplifies
substantially the proofs, not only of elementary theorems, but also of deep results” (Kurt
Gödel).
Einen ersten Eindruck über die Tragweite von Nichtstandardmethoden vermitteln die Bücher (1) und (2).
Literatur:
Typisches Semester: | ab 4. Semester |
Notwendige Vorkenntnisse: | Grundvorlesungen in Linearer Algebra und Analysis. |
Kommentar: | Prüfungsrelevanz: in Verbindungen mit anderen Vorlesungen im Hauptdiplom und Staatsexamen |