Stand: 4.07.2006

Hinweise der Studienberater

Allen Studierenden der Mathematik wird empfohlen, spätestens ab Beginn des 3. Semesters wegen einer sinnvollen Planung des weiteren Studiums die Studienberatung in den einzelnen Abteilungen des Mathematischen Instituts in Anspruch zu nehmen.

Unabhängig hiervon sollte jede Studentin (jeder Student) unmittelbar nach abgeschlossenem Vordiplom (Zwischenprüfung) einen oder mehrere Dozenten der Mathematik aufsuchen, um mit diesem über die Gestaltung des zweiten Studienabschnitts zu sprechen und sich über die Wahl des Studienschwerpunkts zu beraten. Hierzu hat die Fakultät ein „Mentorenprogramm“ eingerichtet, im Rahmen dessen die Studierenden der Mathematik ab dem dritten Fachsemester von Dozenten zu Beratungsgesprächen eingeladen werden. Die Teilnahme an diesem Programm wird nachdrücklich empfohlen.

Hingewiesen sei auch auf die Studienpläne der Fakultät für Mathematik und Physik zu den einzelnen Studiengängen (Diplom, Baccalaureat, Staatsexamen, Magister Artium und Magister Scientiarum; siehe z.B. http://www.math.uni-freiburg.de/lehre/studiengaenge.de.html). Sie enthalten Informationen über die Schwerpunktgebiete in Mathematik sowie Empfehlungen zur Organisation des Studiums. Empfohlen werden die „Hinweise zu den Prüfungen in Mathematik“. Sie enthalten zahlreiche Informationen zu Prüfungen.

Inwieweit der Stoff mittlerer oder höherer Vorlesungen für Diplom– oder Staatsexamensprüfungen ausreicht bzw. ergänzt werden sollte, geht entweder aus den Kommentaren hervor oder muss rechtzeitig mit den Prüfern abgesprochen werden. Zum besseren Verständnis der Anforderungen der einzelnen Studienschwerpunkte wird ein Auszug aus dem Studienplan für den Diplom-Studiengang abgedruckt. Beachten Sie bitte, dass die Teilnahme an Seminaren in der Regel den vorherigen Besuch einer oder mehrerer Kurs– oder Spezialvorlesungen voraussetzt. Die Auswahl dieser Vorlesungen sollte rechtzeitig erfolgen. Eine Beratung durch Dozenten oder Studienberater der Mathematik erleichtert die Auswahl.

Inhaltsverzeichnis
Orientierungsprüfung
Vordiplom, Zwischenprüfung
Sprechstunden
Arbeitsgebiete
1 Vorlesungen
 1.1 Analysis III
 1.2 Algebra
 1.3 Einführung in die Stochastik
 1.4 Numerik I
 1.5 Algebraische Geometrie I
 1.6 Analytische Zahlentheorie
 1.7 Mengenlehre
 1.8 Wahrscheinlichkeitstheorie II
 1.9 Theorie und Numerik partieller Differentialgleichungen I
 1.10 Funktionalanalysis
 1.11 Didaktik der Geometrie und der Stochastik
 1.12 Die Ramanujan-Konstante e^π
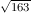
 1.13 Morsetheorie
 1.14 Mathematische Statistik
 1.15 Theorie und Numerik partieller Differentialgleichungen III
 1.16 Futures and Options
 1.17 Informatik im Kontext von Recht, Genderforschung und Design.
 1.18 Average-Case Analyse
2 Praktika
 2.1 Statistisches Praktikum
 2.2 Numerik I
 2.3 Theorie und Numerik partieller Differentialgleichungen I
3 Proseminare
 3.1 Geometrie
 3.2 Flächen
 3.3 Zahlentheoretische Funktionen
 3.4 Über das BUCH der Beweise
4 Seminare
 4.1 Geometrische Analysis
 4.2 Gleichverteilung
 4.3 Untergruppenwachstum
 4.4 Zahlentheorie
 4.5 Logik und Komplexität
 4.6 Modelltheorie
 4.7 Stochastische Analyse
 4.8 Seminar zur Stochastik
 4.9 Geometrische Differentialgleichungen
 4.10 Numerik für konvektionsdominante Differentialgleichungen
 4.11 Strömungsdynamik
 4.12 Numerik elliptischer Differentialgleichungen
 4.13 Social Navigation für CSCW
 4.14 Professional Skills for Computer Scientists
 4.15 Teamarbeit - face to face und virtuell: Basics, Methoden, Anforderungen
 4.16 E-Learning zwischen technischen Anforderungen und NutzerInnenanforderungen
 4.17 Hirnbilder - Geschlechterbilder
 4.18 KörperGeschlechter: Konstruktionen im Wechselspiel Nature-Culture
 4.19 SexEcology
 4.20 Differentialgeometrie
 4.21 Oberseminar über Angewandte Mathemtik
 4.22 Medizinische Statistik
5 Arbeitsgemeinschaften
 5.1 Kobordismus
 5.2 Geometrische Analysis
 5.3 Algebra
 5.4 Nicht-Newtonsche Flüssigkeiten
 5.5 Computereinsatz im Mathematikunterricht
 5.6 Forschungsprojekte-DoktorandInnenseminar
6 Kolloquia
 6.1 Kolloquium