[next] [prev] [prev-tail] [tail] [up]

1.15 Theorie und Numerik partieller Differentialgleichungen III

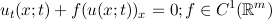
Vorlesung:

Theorie und Numerik partieller Differentialgleichungen III

  

Dozent:

Dr. A. Dedner, Dr. M. Ohlberger

  

Zeit/Ort:

Di, Do 9-11, SR 226 Hermann-Herder-Str. 10

  

Inhalt:

Wesentliche zeitabhängige Prozesse in der Strömungs- und Festkörpermechanik, aber auch in der Elektrodynamik und Relativitätstheorie werden durch nichtlineare Systeme partieller Differentialgleichungen vom Typ des Erhaltungssatzes beschrieben. Vernachlässigt man alle Effekte höherer Ordnung wie Reibung, elektrischen Widerstand, Kapillarkräfte usw., läßt sich diese Klasse von Differentialgleichungen für die vektorwertige Unbekannte u = u(x;t) ∈ ℝm,m ∈ ℕ in einer Raumdimension in der Form

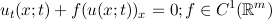
u (x;t)+ f(u(x;t)) = 0;f ∈ C1(ℝm) t x
schreiben. In der Vorlesung werden wir Erhaltungssätze vom Standpunkt der Analysis und der Numerik studieren. Besonderer Schwerpunkt wird der Bezug zu Anwendungen aus den oben genannten Gebieten sein. Die Vorlesung setzt die Vorlesung Numerik partieller Differentialgleichungen II fort, in der der skalare Fall m = 1 behandelt wurde. Aufbauend auf dem Stoff können Diplomarbeiten vergeben werden.

Literatur:

  1. D. Kröner: Numerical schemes for conservation laws, Wiley und Teubner, Chichester, Stuttgart, 1997.

Typisches Semester:

7. Semester

Studienschwerpunkt:

Angewandte Mathematik

Notwendige Vorkenntnisse:

Theorie und Numerik für partieller Differentialgleichungen II

Nützliche Vorkenntnisse:

Funktionalanalysis

Sprechstunde Dozent:

n.V.

[next] [prev] [prev-tail] [front] [up]