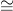5.1 Kobordismus

Inhalt:

Kompakte, zusammenhängende differenzierbare Mannigfaltigkeiten der Dimension ≥ 5 lassen sich mit topologischen Methoden zumindest grob klassifizieren. In dieser AG wollen wir die ersten Schritte auf dem Wege zu dieser Klassifizierung studieren. Der genaue Inhalt der AG richtet sich nach Interesse und Vorkenntnissen der Teilnehmer.

Am Anfang steht die Bordismusklassifikation. Zwei Mannigfaltigkeiten M₀, M₁ heißen “kobordant”, wenn es eine Mannigfaltigkeit W mit Rand M₀ ∪M₁ gibt. Die charakteristischen Klassen und Zahlen von M₀ und M₁ geben Auskunft, ob das möglich ist.

Wenn zwei Mannigfaltigkeiten kobordant sind, kann man versuchen, die obige Mannigfaltigkeit W so weit wie möglich zu vereinfachen — am liebsten hätte man W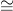M₀ × [0, 1], denn dann wäre M₀ = M₁. Ein Hindernis auf dem Weg dorthin ist die Whitehead-Torsion.

Paradebeispiel dieser Theorie sind die “exotischen Sphären” ab Dimension n ≥ 7, die topologisch, aber nicht differenzierbar isomorph zur Sⁿ sind.

Literatur:

1. Kosinski, A.: Differential manifolds, Acad. Press, Boston, 1993.
2. Milnor, J.: Lectures on the h-cobordism theorem, Princeton Univ. Press, Princeton, 1965.
3. ——, Stasheff, J.: Characteristic Classes, Ann. Math. Stud. 76, Princeton Univ. Press, Princeton, 1974.