4.9 Geometrische Differentialgleichungen
Seminar: | Geometrische Differentialgleichungen |
| | |
Dozent: | Prof. Dr. Gerhard Dziuk |
| | |
Zeit/Ort: | Mi. 14-16 Uhr, SR 226, Hermann-Herder-Str. 10 |
| | |
Tutorium: | Paola Pozzi, PhD |
| | |
Vorbesprechung: | Mi. 26. 7. 2006, 13.15 Uhr, SR 226, Hermann-Herder-Str.
10 |
| | |
Teilnehmerliste: | Bei Frau Ruf, Raum 205, Hermann-Herder-Str. 10 |
| | |
Web-Seite: | http://aam.mathematik.uni-freiburg.de/IAM/ |
| | |
| |
Inhalt:
Dieses Seminar richtet sich an Studierende, die sowohl an der Analysis/Geometrie als auch an
der Numerik interessiert sind. Wir werden uns vor allem mit einem Problem vierter Ordnung
befassen, das sowohl theoretisch als auch praktisch von Interesse ist. Die Biegeenergie einer
Fläche Γ, Willmore-Funktional genannt, ist 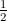 ∫
ΓH2, wobei H die mittlere Krümmung der
Fläche bezeichnet. Von besonderem Interesse ist der erst in den letzten Jahren analytisch
untersuchte Willmorefluss. Das ist die Methode des steilsten Abstiegs zum Willmore-Funktional.
Schon bei Kurven und erst recht bei Flächen ist die Bewegung während dieser Minimierung der
elastischen Energie spannend und mathematisch äußerst interessant; auch ist dieser Fluss auch
für zahlreiche Anwendungen (Physik, Bildverarbeitung) von besonderem Interesse.
∫
ΓH2, wobei H die mittlere Krümmung der
Fläche bezeichnet. Von besonderem Interesse ist der erst in den letzten Jahren analytisch
untersuchte Willmorefluss. Das ist die Methode des steilsten Abstiegs zum Willmore-Funktional.
Schon bei Kurven und erst recht bei Flächen ist die Bewegung während dieser Minimierung der
elastischen Energie spannend und mathematisch äußerst interessant; auch ist dieser Fluss auch
für zahlreiche Anwendungen (Physik, Bildverarbeitung) von besonderem Interesse.
Die Grundbegriffe aus der Differentialgeometrie und der geometrischen Analysis werden
während des Seminars bereitgestellt bzw. wiederholt. Danach werden wir Eigenschaften des
Energiefunktionals für Flächen herleiten. Schließlich sollen die analytischen Resultate so
aufbereitet werden, dass sie sich zur numerischen Simulation des Willmore-Flusses eignen.
Bei Interesse können auch praktische Vorträge vergeben werden. Dazu sind Vorkenntnisse bei
der Anwendung der Finite-Elemente-Methode notwendig.
Dieses Seminar kann zu Diplom- oder Staatsexamensarbeiten führen.
Literatur:
- Computation of geometric partial differential equations and mean curvature flow (K.
Deckelnick, G. Dziuk, C. M. Elliott). Acta Numerica (2005), 139–232.
Typisches Semester: | ab 5. Semester |
Studienschwerpunkt: | Angewandte Mathematik |
Notwendige Vorkenntnisse: | Analysis III |
Nützliche Vorkenntnisse: | Theorie und Numerik partieller Differentialgleichungen,
Differentialgeometrie |
Sprechstunde Dozent: | Mi. 11.30–12.30, Raum 209, H.-H.-Str. 10 und n. V. |
Sprechstunde Assistentin: | Mo. 14–15, Raum 213, H.-H.-Str. 10 und n. V. |
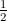 ∫
ΓH2, wobei H die mittlere Krümmung der
Fläche bezeichnet. Von besonderem Interesse ist der erst in den letzten Jahren analytisch
untersuchte Willmorefluss. Das ist die Methode des steilsten Abstiegs zum Willmore-Funktional.
Schon bei Kurven und erst recht bei Flächen ist die Bewegung während dieser Minimierung der
elastischen Energie spannend und mathematisch äußerst interessant; auch ist dieser Fluss auch
für zahlreiche Anwendungen (Physik, Bildverarbeitung) von besonderem Interesse.
∫
ΓH2, wobei H die mittlere Krümmung der
Fläche bezeichnet. Von besonderem Interesse ist der erst in den letzten Jahren analytisch
untersuchte Willmorefluss. Das ist die Methode des steilsten Abstiegs zum Willmore-Funktional.
Schon bei Kurven und erst recht bei Flächen ist die Bewegung während dieser Minimierung der
elastischen Energie spannend und mathematisch äußerst interessant; auch ist dieser Fluss auch
für zahlreiche Anwendungen (Physik, Bildverarbeitung) von besonderem Interesse.