1.12 Die Ramanujan-Konstante e^π

Inhalt:

S. A. Ramanujan entdeckte, daß die (nach Siegel-Gelfond-Schneider transzendente) Zahl e^π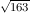 bis auf einen Fehler ≤ 10^-12 bemerkenswert nahe bei der ganzen Zahl 262.537.412.640.768.744 liegt.

Wir werden in dieser Vorlesung einen nichtnumerischen Beweis erarbeiten und dafür einschlägige Sätze über Endomorphismenring und j-Invariante einer elliptischen Kurve und über modulare Formen studieren. Entscheidend wird sein: Ist der Endomorphismenring einer elliptischen Kurve der Ganzheitsring eines imaginärquadratischen Zahlkörpers mit Klassenzahl 1 (hier nämlich ℚ(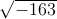)), so ist ihre j-Invariante ganzzahlig.

Um unser Ziel zu erreichen, verwenden wir öfters Begriffe aus der Funktionentheorie, Algebra, der algebraischen und analytischen Zahlentheorie. Diese sind geläufig bzw. werden erarbeitet, falls Bedarf besteht. Letztlich ist das Studium der Ramanujan-Konstante ein schönes Beispiel dafür, wie verschiedene Bereiche der reinen Mathematik zu einem gemeinsamen Thema beitragen können.

Zu Beginn der Vorlesung werfen wir außerdem einen Blick in die Biographien von G. H. Hardy und S. A. Ramanujan.

Literatur:

1. B. J. Green: The Ramanujan Constant, ein Essay erhältlich unter
   http://www-math.mit.edu/green/notes.html