
![Studierende vorm Mathematischen Institut
(Foto: Martin Kramer, © Mathematisches Institut Freiburg) [Studierende vorm Mathematischen Institut]](https://www.math.uni-freiburg.de//i/Webseite-oben-Studierende_vorm_Mathematischen_Institut.jpg)
Zurück zur Überblicksseite „Informationen für Studieninteressierte“.
Für den Studienanfang gibt es zwei Bachelor-Studiengänge in Mathematik. Bei beiden beginnt das Studium im Wintersemester. Ein Wechsel ist innerhalb der ersten ein, zwei Jahre gut möglich, da sie eine große Überschneidung im Studienprogramm in Mathematik haben.
Für das Weiterstudium gibt es die beiden Studiengänge:
Für Mathematik als Drittfach im Lehramtsstudium gibt es den Studiengang:
Beide Bachelor-Studiengänge beginnen mit grundlegenden Vorlesungen in Analysis und Linearer Algebra. Darauf aufbauend gibt es verpflichtende Einführungen in einige Teilgebiete der Mathematik, ergänzt durch ein Proseminar und Praktische Übungen (Computerübungen). Im B.Sc.-Studiengang folgen mehrere weiterführende Wahlvorlesungen.
Beispielhafter Studienverlauf im Bachelor-of-Science-Studiengang Mathematik:
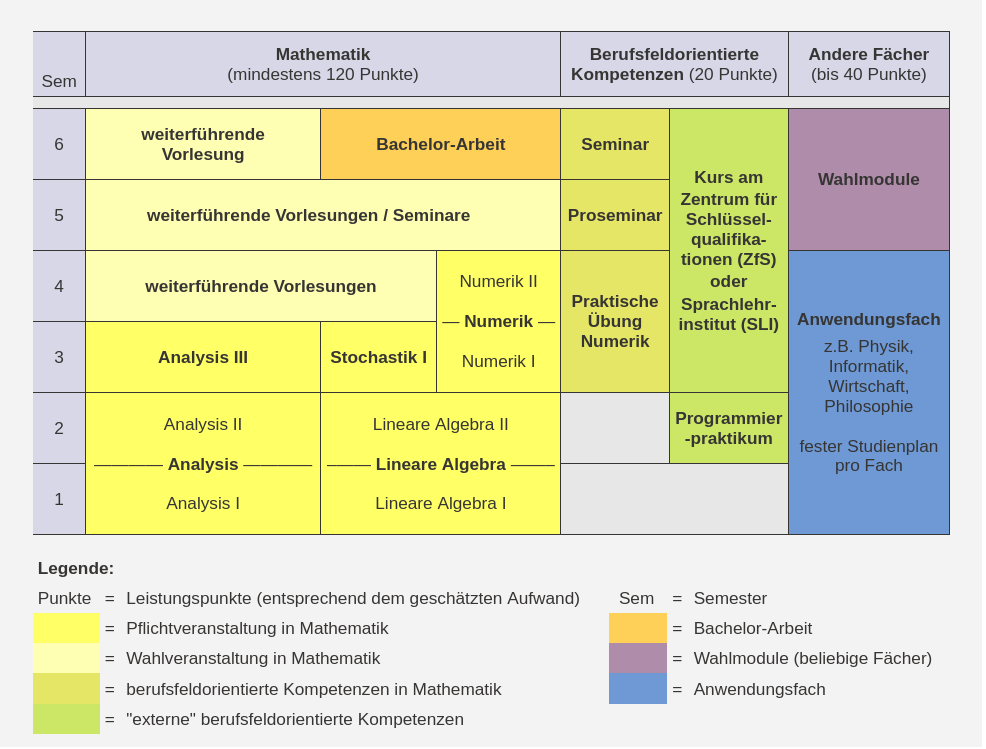
Unter Beachtung der Vorkenntnisse kann man die Reihenfolge der Veranstaltungen umstellen, insbesondere in den höheren Semestern. Zusammen mit den Wahlmöglichkeiten bei Veranstaltungen ergeben sich so viele Freiheiten zur individuellen Studiengestaltung. Im Zwei-Hauptfächer-Bachelor-Studiengang sind die Studieninhalte dagegen weitgehend vorgeschrieben.
Beispielhafter Studienverlauf im Zwei-Hauptfächer-Bachelor-Studiengang Mathematik:
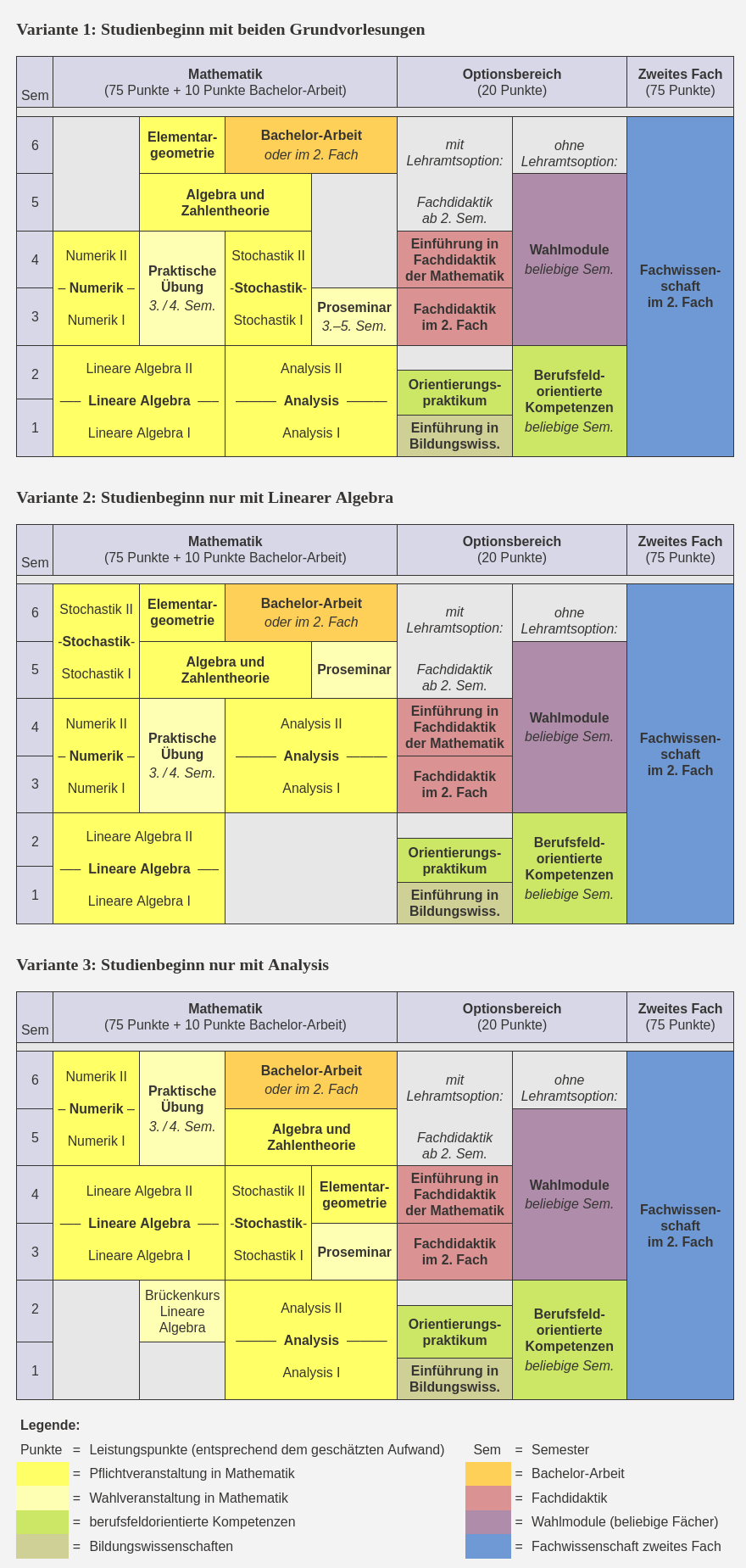
Abhängig vom zweiten Fach kann man entweder mit beiden Grunbdvorlesungen in Analysis und Linearer Algebra beginnen oder nur mit einer von beiden. Die weiterführenden Vorlesungen und Veranstaltungen bauen teilweise inhaltlich auf diesen Grundvorlesungen auf, können aber unter Berücksichtigung der notwendigen Vorkenntnisse beliebig auf die Semester verteilt werden.
Die Freiburger Mathematik teilt sich auf sechs Bereiche auf, die untereinander mehr oder weniger starke Berührungspunkte haben:
Vertreten durch Kooperationen mit Mathematiker:inne:n aus anderen Fakultäten sind außerdem die Gebiete:
Detailliertere Informationen finden Sie auf der Seite:
Dozenten/Dozentinnen und ihre Schwerpunktgebiete.