Master of Science in Mathematics (regulations of 2014)

The degree programme has an official duration of two years. It is taught in German (however, advanced courses might be taught in English on request and course material in English can be made available). Students are almost completely free to choose among our courses and may specialise in any of our areas of expertise:

• Algebra and Number Theory
• Analysis
• Applied Analysis and Numerical Mathematics
• Geometry and Topology
• Mathematical Logic (set theory / model theory)
• Mathematical Stochastics and Financial Mathematics

The specialisation in Financial Mathematics will be emphasised on the examination certificate.

In case of questiosn concerning application, pleasye contact the academic advise of the Mathematical Institute (studienberatung@math.uni-freiburg.de

It is possible to apply for the winter term (lectures starting in mid-October) and for the summer term (lectures starting in mid-April).

The application period is approx. 15 May to 15 July for the winter term, and approx. 15 November to 15 January for the summer term. (Sometimes, opening of the application portal is delayed for soime days.)

Application process

1. If not yet student at our university, register first as applicant via the portal HISinOne
2. Prepare all necessary documents as pdf or jpg file (5 MB maximum each) — see list below. Please use file names of the form Family_name-Type_of_document, e.g. Smith-Transcript_of_Records.pdf.
3. Beginning at the first day of the application period, you can enter your application in HISinOne and upload the necessary documents. Please keep the originals ready, they will be asked for at matriculation (enrolment).
4. Print the confirmation form produced by HISinOne, sign it, scan it, and upload it. Then submit your application.
5. After the deadline, the admission committee meets and decides about the mathematical requirements. International Admissions and Services (IAS) checks the language proofs and university degrees.
   We try to inform you as soon as possible via the application portal or e-mail about the results.
   For questions, please contact studienberatung@math.uni-freiburg.de.
6. Your need your diploma certificate for matriculation (enrolment), not yet for application.

Documents needed

1. A transcript of records, if necessary* with translation.
2. The diploma certificate of your first university degree on the basis of which you apply for the Master's degree programme (typically a Bachelor's degree in Mathematics), if necessary* with translation.
   In case the degree is not yet finished and no information about the final thesis is found on the transcript of records: A confirmation from your university about grading, submission, declaration or registration of your final thesis, if applicable, or otherwise about the expected date of graduation.
3. For applicants from China, Vietnam and Mongolia: the APS certificate.
4. Proof of your language proficiency in German: at least level B2 (accepted proofs).
5. Proof of your language proficiency in English: at least level B1 (accepted proofs).
6. The signed confirmation form (produced by HISinOne during the application procedure).

* Documents not in German, English or French must be translated into German or English either by a sworn translator or the translation has to be approved by a German Embassy or Consulate.

(1) A Bachelor's degree in mathematics that is officially recognised in Germany or an equivalent degree, satisfying the following conditions:
An equivalent of at least 103 ECTS credits in courses in mathematics (possibly includin a Bachelor's thesis in Mathematics), among them at least 16 credits from each of

• basic courses in analysis,
• basic courses in linear algebra,
• courses in pure mathematics,
• courses in applied mathematics.

(2) Language proficiency: B2 in German and B1 in English (accepted proofs).

The admission committee decides whether the mathematical conditions are considered to be fulfilled and on exceptions from special conditions (e.g. if the Bachelor's degree programme is designed without the requirement of a Bachelor's thesis). Before the meeting of the admission committee, we can give no reliable information about the likely success of an application. Recognition of language proofs and international degrees is ruled by legal requirements and is checked by International Admissions and Services.

Please note that this page is only for your information. Admission is subject to the legal admissions regulations.

Computer systems:

• student information system HISinOne with instruction manual in the Campus Management Wiki
• learning management system ILIAS
• myAccount: administration of your university computer account

Courses:

• teaching periods
• course catalog in mathematics with comments
• course catalog of the university in HISinOne
• Eucor – The European Campus / Le Campus Européen
• language teaching centre (SLI)
• studium generale

Module handbook and related material:

• module handbooks with requirements for credit points in each course
• specializations:
  – specialization in finanical mathematics: see below
  – academic staff with research fields
  – study patters in the various specializations (with prerequisites for a Master's thesis)
  – synopsis of the regularly taught courses in mathematics (pdf)
• Information about the Master's thesis

Examinations and regulations:

• registration periods
• examination office
• examination regulations

Further topics:

• research groups at the institute
• guide for international students (pdf)

The degree programme has a normal length of 4 semester with 120 credit points to be completed. It comprises the following parts:

• modules based on lectures, with oral examinations (54 credits)
• seminars (12 credits)
• electives in mathematics (9 to 21 credits)
• electives in other subjects (up to 12 credits)
• master's thesis with presentation (33 credits)

If you opt for the specialization in Financial Mathematics, all electives have to be chosen among special electives in economics.

Possible route of study:

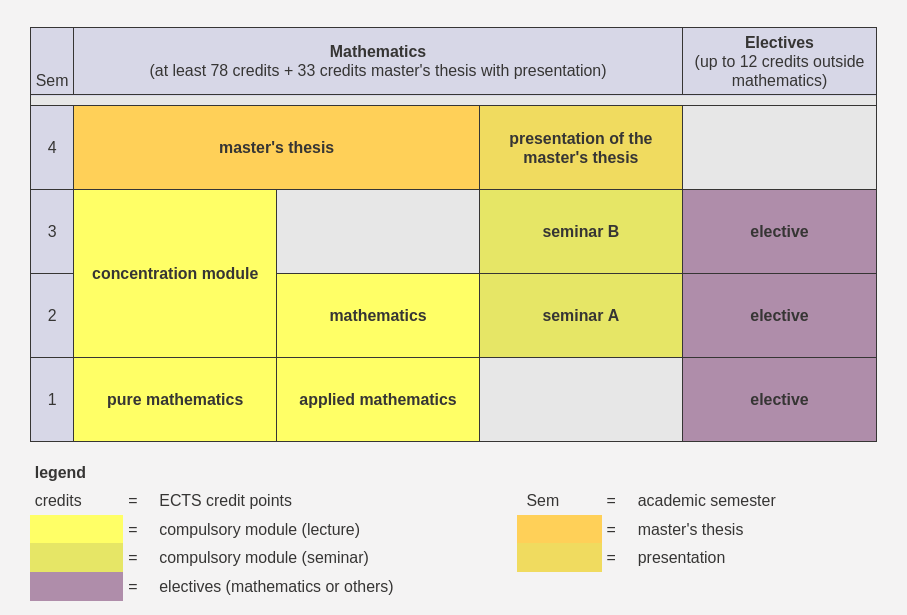
This plan is only an indication and guidance. Except for admission to the master's thesis (60 credit points minimum), there are no rules for the modules, you can place them arbitrarily in the course of study. Be aware of the prerequisites of the chosen courses, however!

Sorry, there is not yet an English translation for this page.

(A) Belegungen von Veranstaltungen:

• Belegungen von Vorlesungen, d.h. Abgabe eines Teilnahmewunschs, können über das Vorlesungsverzeichnis in HISinOne (Menüpunkt 'Veranstaltungen suchen') ab September bzw. März erfolgen.
• Die Anmeldung zu Übungsgruppen/Tutoraten erfolgt nach dem in der Vorlesung bekanntgegebenen Verfahren in der ersten Vorlesungswoche.
• Studienpätze für Seminare werden bei der Vorbesprechung am Ende der Vorsemesters vergeben. Die Termine dafür und ggf. die Art der Voranmeldung sind im Kommentierten Vorlesungsverzeichnis angegeben.
  Es gibt keine Belegung über HISinOne, aber die fristgerechte Anmeldung der Prüfung ist erforderlich!
• Für die Teilnahme am Modul "Fachdidaktische Forschung" ist eine separate Anmeldung über die Abteilung für Didaktik der Mathematik erforderlich.

Welche Veranstaltungen für Module mit Wahlmöglichkeiten in Frage kommen, ist im Kommentierten Vorlesungs­verzeichnis und in den aktuellen Ergänzungen der Modulhandbücher beschrieben. Kompakt findet sich die Information in den Verwendungstabellen.

(B) Anmeldungen von Prüfungen und Registrierung von Studienleistungen:

• Alle Prüfungen müssen vor Ablegen der Prüfung angemeldet werden und alle Studienleistungen registriert werden. Bis auf wenige Ausnahmen geht dies über den Studienplaner in HISinOne
• Achtung: Die Belegung einer Veranstaltung ersetzt nicht die Anmeldung der Prüfung bzw. Registrierung der Studienleistung! Insbesondere ist mit der Zuteilung zu einer Übungsgruppe zu Vorlesungsbeginn noch nicht die „Studienleistung Übung“ registriert!
• Vor der Anmeldung der ersten Prüfungsleistung müssen Sie beim Prüfungsamt einen Antrag auf Zulassung zu den studienbegleitenden Prüfungen im Master stellen. Das Prüfungsamt braucht dazu eine vollständige Leistungsübersicht aus Ihrem zugrundeliegenden Bachelor-Studiengang.

Die genauen Anforderungen an Prüfungs- und Studienleistungen sind semesterweise in den aktuellen Ergänzungen der Modulhandbücher beschrieben.

Anleitung für die Prüfungsanmeldung / SL-Registrierung in HISinOne (siehe auch HISinOne-Wiki): In HISinOne 'Mein Studium > Studienplaner mit Modulplan' (ggf. mit richtigem Studiengang) auswählen. Links oben das richtige Semester auswählen und rechts oben bei Veranstaltungen 'keine' und bei Prüfungs-/Studienleistungen 'alle' anklicken. Dann in der Liste das gewünschte Modul bzw. die gewünschte Veranstaltung suchen. Auf 'Prüfung anmelden' bzw. 'Studienleistung registrieren' gehen. Gegebenenfalls noch die richtige Gruppe auswählen.

(C) Modulplan mit Erläuterungen:
Alle hier im Überblick gegebenen Informationen finden sich ausführlicher im Modulhandbuch.

1. VORLESUNGSMODULE    (54 ECTS-Punkte)
Modulteil	Nummer in HISinOne	Angebot / Zeitpunkt	Anmeldung
REINE MATHEMATIK    (Pflichtmodul mit Wahlveranstaltung, 11 ECTS-Punkte)
Voraussetzungen
Die notwendigen Vorkenntnissen hängen von der gewählten Vorlesung ab, siehe Kommentiertes Vorlesungs­verzeichnis.
Veranstaltungen
4-stündige Vorlesung oder zwei 2-stündige Vorlesungen aus der Reinen Mathematik	07LE23V-?-??	jedes Semester	Belegung der Vorlesung bis Vorlesungsbeginn Belegung der Übung in der Regel in der ersten Vorlesungswoche
zu jeder Vorlesung in der Regel 2-stündige Übung	07LE23Ü-?-??
Studienleistungen
zu jeder Vorlesung Kategorie II: – Übung – Klausur	07LE23SL-Ü-?-?? 07LE23SL-K-?-??	im jeweiligen Semester	Registrierung bis Fristende im Wintersemester
zu jeder Vorlesung Kategorie III: – Übung mit ggf. Klausur/Prüfung	07LE23SL-?E-?-??
Prüfungsleistungen
mündliche Prüfung über alle Modulteile Dauer: 30 Minuten	07LE23PL-MSc14-P-RM	nach individueller Terminvereinbarung mit Prüfer:in	Anmeldung spätestens drei Wochen vor Prüfung schriftlich im Prüfungs­amt (Formular)
Bemerkungen
Welche Vorlesungen zur Reinen Mathematik gezählt werden und für das Modul zugelassen sind, ist im Kommentierten Vorlesungs­verzeichnis und in den aktuellen Ergänzungen der Modulhandbücher beschrieben. Kompakt findet sich die Information in den Verwendungstabellen. 2-stündige Vorlesungen gehen mit 4,5 ECTS-Punkten in das Modul ein, unabhängig vom Umfang der Übungen, also unabhängig davon, wie viele ECTS-Punkte sie als Wahlmodul bekommen. Die Zusammensetzung der Moduls aus 2-stündigen Vorlesungen ist mit dem/der Prüfer:in abzusprechen. Das Modul kann auch von zwei Prüfer:inne:n geprüft werden. In maximal zwei der vier Vorlesungsmodule darf der/die selbe Prüfer:in prüfen.
ANGEWANDTE MATHEMATIK    (Pflichtmodul mit Wahlveranstaltung, 11 ECTS-Punkte)
Voraussetzungen
Die notwendigen Vorkenntnissen hängen von der gewählten Vorlesung ab, siehe Kommentiertes Vorlesungs­verzeichnis.
Veranstaltungen
4-stündige Vorlesung oder zwei 2-stündige Vorlesungen aus der Angewandten Mathematik	07LE23V-?-??	jedes Semester	Belegung der Vorlesung bis Vorlesungsbeginn Belegung der Übung in der Regel in der ersten Vorlesungswoche
zu jeder Vorlesung in der Regel 2-stündige Übung	07LE23Ü-?-??
Studienleistungen
zu jeder Vorlesung Kategorie II: – Übung – Klausur	07LE23SL-Ü-?-?? 07LE23SL-K-?-??	im jeweiligen Semester	Registrierung bis Fristende im Wintersemester
zu jeder Vorlesung Kategorie III: – Übung mit ggf. Klausur/Prüfung	07LE23SL-?E-?-??
Prüfungsleistungen
mündliche Prüfung über alle Modulteile Dauer: 30 Minuten	07LE23PL-MSc14-P-AM	nach individueller Terminvereinbarung mit Prüfer:in	Anmeldung spätestens drei Wochen vor Prüfung schriftlich im Prüfungs­amt (Formular)
Bemerkungen
Welche Vorlesungen zur Angewandten Mathematik gezählt werden und für das Modul zugelassen sind, ist im Kommentierten Vorlesungs­verzeichnis und in den aktuellen Ergänzungen der Modulhandbücher beschrieben. Kompakt findet sich die Information in den Verwendungstabellen. 2-stündige Vorlesungen gehen mit 4,5 ECTS-Punkten in das Modul ein, unabhängig vom Umfang der Übungen, also unabhängig davon, wie viele ECTS-Punkte sie als Wahlmodul bekommen. Die Zusammensetzung der Moduls aus 2-stündigen Vorlesungen ist mit dem/der Prüfer:in abzusprechen. Das Modul kann auch von zwei Prüfer:inne:n geprüft werden. In maximal zwei der vier Vorlesungsmodule darf der/die selbe Prüfer:in prüfen.
MATHEMATIK    (Pflichtmodul mit Wahlveranstaltung, 11 ECTS-Punkte)
Voraussetzungen
Die notwendigen Vorkenntnissen hängen von der gewählten Vorlesung ab, siehe Kommentiertes Vorlesungs­verzeichnis, oder vom konkreten Lesekurs. Lesekurse werden in individueller Absprache mit einem/einer Dozent:in angeboten und erscheinen nicht im Vorlesungsverzeichnis.
Veranstaltungen
4-stündige Vorlesung oder zwei 2-stündige Vorlesungen jeweils Kategorie III	07LE23V-?-??	jedes Semester	Belegung der Vorlesung bis Vorlesungsbeginn
zu jeder Vorlesung in der Regel 2-stündige Übung	07LE23Ü-?-??		Belegung der Übung in der Regel in der ersten Vorlesungswoche
alternativ: Lesekurs (= betreutes Selbst­studium) im Umfang einer 4-stündigen Vorlesung	(nicht in HISinOne)		Belegung eines Lesekurses durch persönliche Anmeldung bei dem/der Dozent:in
Studienleistungen
zu jeder Vorlesung: Übung mit ggf. Klausur/Prüfung	07LE23SL-?E-?-??	im jeweiligen Semester	Registrierung bis Fristende im Wintersemester
zum Lesekurs: Studienleistungen wie abgesprochen	07LE23SL-MSc14-P-M_WA
Prüfungsleistungen
mündliche Prüfung über alle Modulteile Dauer: 30 Minuten	07LE23PL-MSc14-P-M	nach individueller Terminvereinbarung mit Prüfer:in	Anmeldung spätestens drei Wochen vor Prüfung schriftlich im Prüfungs­amt (Formular)
Bemerkungen
Welche Vorlesungen zur Kategorie III zählen, ist im Kommentierten Vorlesungs­verzeichnis und in den aktuellen Ergänzungen der Modulhandbücher beschrieben. Kompakt findet sich die Information in den Verwendungstabellen. 2-stündige Vorlesungen gehen mit 4,5 ECTS-Punkten in das Modul ein, unabhängig vom Umfang der Übungen, also unabhängig davon, wie viele ECTS-Punkte sie als Wahlmodul bekommen. Die Zusammensetzung der Moduls aus 2-stündigen Vorlesungen ist mit dem/der Prüfer:in abzusprechen. Das Modul kann auch von zwei Prüfer:inne:n geprüft werden. In maximal zwei der vier Vorlesungsmodule darf der/die selbe Prüfer:in prüfen.
VERTIEFUNSGMODUL    (Pflichtmodul mit Wahlveranstaltung, 21 ECTS-Punkte)
Voraussetzungen
Die notwendigen Vorkenntnissen hängen von den gewählten Vorlesungen ab, siehe Kommentiertes Vorlesungs­verzeichnis, oder von den konkreten Lesekursen. Lesekurse werden in individueller Absprache mit einem/einer Dozent:in angeboten und erscheinen nicht im Vorlesungsverzeichnis.
Veranstaltungen
zwei 4-stündige Vorlesung oder statt jeder 4-stündigen: zwei 2-stündige Vorlesungen jeweils Kategorie III	07LE23V-?-??	jedes Semester	Belegung der Vorlesung bis Vorlesungsbeginn
zu jeder Vorlesung in der Regel 2-stündige Übung	07LE23Ü-?-??		Belegung der Übung in der Regel in der ersten Vorlesungswoche
alternativ statt jeder 4-stündigen Vorlesung: Lesekurs (= betreutes Selbst­studium) im Umfang einer 4-stündigen Vorlesung	(nicht in HISinOne)		Belegung eines Lesekurses durch persönliche Anmeldung bei dem/der Dozent:in
Studienleistungen
zu jeder Vorlesung: Übung mit ggf. Klausur/Prüfung	07LE23SL-?E-?-??	im jeweiligen Semester	Registrierung bis Fristende im Wintersemester
zum Lesekurs: Studienleistungen wie abgesprochen	07LE23SL-MSc14-P-VM_WA_?
Prüfungsleistungen
mündliche Prüfung über alle Modulteile Dauer: 45 Minuten	07LE23PL-MSc14-P-VM	nach individueller Terminvereinbarung mit Prüfer:in	Anmeldung spätestens drei Wochen vor Prüfung schriftlich im Prüfungs­amt (Formular)
Bemerkungen
Welche Vorlesungen zur Kategorie III zählen, ist im Kommentierten Vorlesungs­verzeichnis und in den aktuellen Ergänzungen der Modulhandbücher beschrieben. Kompakt findet sich die Information in den Verwendungstabellen. 2-stündige Vorlesungen gehen mit 4,5 ECTS-Punkten in das Modul ein, unabhängig vom Umfang der Übungen, also unabhängig davon, wie viele ECTS-Punkte sie als Wahlmodul bekommen. Die Zusammensetzung der Moduls ist mit dem/der Prüfer:in abzusprechen; die Modulteile sollten eine inhaltliche Nähe und ein angemessenes Niveau aufweisen. Das Modul kann auch von zwei Prüfer:inne:n geprüft werden. In maximal zwei der vier Vorlesungsmodule darf der/die selbe Prüfer:in prüfen.
2. SEMINARE    (12 ECTS-Punkte)
Modulteil	Nummer in HISinOne	Angebot / Zeitpunkt	Anmeldung
MATHEMATISCHES SEMINAR A    (Pflichtmodul mit Wahlveranstaltung, 6 ECTS-Punkte)
Voraussetzungen
Die notwendigen Vorkenntnissen hängen vom gewählten Seminar ab, siehe Kommentiertes Vorlesungs­verzeichnis.
Veranstaltungen
Seminar (2-stündig)	07LE23S-x-?? (x ≠ 7)	jedes Semester	Voranmeldung nach Angaben im Komm. Vorlesungsverzeichnis; Sudienplatzvergabe bei der Vorbesprechung am Ende des Vorsemesters
Studienleistungen
regelmäßige Anwesenheit und aktive Mitarbeit	07LE23SL-MSc14-P-SemA	im jeweiligen Semester	keine separate Registrierung
Prüfungsleistungen
Vortrag Dauer: ca. 90 Minuten	07LE23PL-MSc14-P-SemA	im jeweiligen Semester	Prüfungsanmeldung bis Fristende vor Vorlesungsbeginn
MATHEMATISCHES SEMINAR B    (Pflichtmodul mit Wahlveranstaltung, 6 ECTS-Punkte)
identisch mit „Mathematisches Seminar A“
Bemerkungen
In den Modulen „Mathematisches Seminar A“ und „Mathematisches Seminar B“ müssen zwei Seminare besucht werden – zwei Vorträge in einem Seminar reichen nicht. Es können allerdings zwei titelgleiche Seminare in verschiedenen Semestern absolviert werden, wenn diese Seminare verschiedenen Inhalt haben.
3. MASTER-MODUL    (Pflichtmodul, 33 ECTS-Punkte)
Voraussetzungen
Voraussetzung für die Zulassung zur Master-Arbeit sind 60 im Studiengang absolvierte ECTS-Punkte. Die inhaltlichen Voraussetzungen müssen mit dem/der Betreuer:in abgesprochen werden.
Prüfungsleistungen
Verfassen der Master-Arbeit Bearbeitungszeit: 6 Monate	07LE23PL-8000-MSc-105-2014	beliebiger Zeitpunkt, in Absprache mit Betreuer:in	Anmeldung schriftlich im Prüfungsamt (Formular)
Studienleistungen
Präsentation der Master-Arbeit Dauer: nicht festgelegt, ca. 60–90 Minuten	07LE23SL-MSc14-P-MMod	beliebiger Zeitpunkt gegen/nach Ende der Bearbeitungszeit, in Absprache mit Betreuer:in	keine separate Anmeldung
Bemerkungen
detaillierte Informationen zu Abschlussarbeiten in Mathematik
4. WAHLMODULE    (21 ECTS-Punkte)
Modulteil	Nummer in HISinOne	Angebot / Zeitpunkt	Anmeldung
Für die Spezialisierung Finanzmathematik (siehe im entsprechenden Abschnitt) gelten gesonderte Bedingungen an die Wahlmodule!
MATHEMATIK-MODULE    (Wahlmodule, mindestens 9 ECTS-Punkte)
Voraussetzungen
Die notwendigen Vorkenntnissen hängen von der gewählten Veranstaltung ab, siehe Kommentiertes Vorlesungs­verzeichnis. Teilnahmebedingung für „Lernen durch Lehren“ ist eine Tutoratsstelle zu einer Vorlesung des Mathematischen Instituts im laufenden Semester (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester).
Veranstaltungen, zur Wahl:
Vorlesung (mit Übung)	07LE23V-?-?? (07LE23Ü-?-??)	jedes Semester	Belegung der Vorlesung bis Vorlesungsbeginn Belegung der Übung in der Regel in der ersten Vorlesungswoche
Praktische Übung	07LE23PÜ-?-??	variabel	Belegung in der Regel in der ersten Vorlesungswoche
Wissenschaftliches Arbeiten (maximal einmal im Wahlmodul)	(nicht in HISinOne)	jedes Semester, nach Absprache mit Dozent:in	Persönliche Anmeldung bei dem/der Dozent:in
Seminar (bis zu vier Seminare – bitte melden Sie sich im Prüfungsamt, wenn Sie die in HISinOne einge­richtete Anzahl überschreiten)	07LE23S-?-??	jedes Semester	Voranmeldung nach Angaben im Komm. Vorlesungsverzeichnis; Sudienplatzvergabe bei der Vorbesprechung am Ende des Vorsemesters
Lernen durch Lehren (maximal zweimal im M.Sc.)	07LE23V-?-??	jedes Semester	Voranmeldung per E-Mail, siehe hier
Studienleistungen
Seminar: Vortrag, regelmäßige Anwesenheit und aktive Mitarbeit	07LE23SL-MSc14-WM6-Sem?	im jeweiligen Semester	Registrierung bis Fristende vor Vorlesungsbeginn
zu jeder Vorlesung Kategorie II: – Übung – Klausur	07LE23SL-Ü-?-?? 07LE23SL-K-?-??	im jeweiligen Semester	Registrierung bis Fristende im jeweiligenemester
zu allen anderen Veranstaltungen gibt es genau eine zu registrierende Studienleistung	07LE23SL-...
Prüfungsleistungen
keine
Bemerkungen
Welche Vorlesungen und Praktischen Übungen als Wahlmodule zugelassen sind, ist im Kommentierten Vorlesungs­verzeichnis und in den aktuellen Ergänzungen der Modulhandbücher beschrieben. Kompakt findet sich die Information in den Verwendungstabellen. Für Wahlmodule werden 21 ECTS-Punkte auf die zu erreichenden 120 ECTS-Punkte angerechnet, es dürfen aber mehr Punkte absolviert werden. Module, die vollständig über dem Soll liegen, werden als Zusatzleistungen ausgewiesen.
MODULE ANDERER FÄCHER    (Wahlmodule, höchstens 12 anrechenbare ECTS-Punkte)
Voraussetzungen
Eventuelle Teilnahmebedingungen und notwendigen Vorkenntnisse hängen von den gewählten Veranstaltungen ab und müssen selbständig in Erfahrung gebracht werden. Insbesondere muss geklärt werden, ob die gewünschte Veranstaltung für fachfremde Studierende offen steht.
Veranstaltungen
Fachfremde Wahlmodule müssen laut Prüfungsordnung „dem Anforderungsniveau der Lehrveranstaltungen des Masterstudiengangs Mathematik entsprechen“ Zugelassen sind insbesondere Veranstaltungen aus einem Master-Studiengang des betreffenden Fachs, Wahlveranstaltungen aus dem dritten Studienjahr eines Bachelor-Studiengangs des betreffenden Fachs, Veranstaltungen, die als wirtschaftswissenschaftliche Spezialisierungsmodule der Spezialisierung „Finanzmathematik“ zugelassen sind. Nicht erlaubt sind Veranstaltungen der Standard-Anwendungsfächer im B.Sc. Mathematik, einführende Veranstaltungen aus den ersten Studienjahren eines Bachelor-Studiengangs, Sprachkurse und BOK-Kurse, insbesondere ZfS-Kurse, Fachdidaktikveranstaltungen, Praktika und Schulpraxis, fachfremde Veranstaltungen, die sich inhaltlich substantiell mit unserem eigenen Angebot überschneiden. Zweifelsfälle müssen vorher geklärt werden; die erfolgreiche Teilnahme an einer Veranstaltung garantiert nicht, dass sie angerechnet werden kann!
Studienleistungen
Für Module – der Technischen Fakultät – der Wirtschaftswissenschaften in der Regel eine zu registrierende Studienleistung	07LE23SL-WF?-??	im jeweiligen Semester	Online-Registrierung bis Ende der Frist des jeweiligen Fachs
	Die Möglichkeit der Online-Registrierung wird bei Bedarf eingerichtet; dazu ist eine rechtzeitige Meldung an die Studiengangkoordination erforderlich.
Für andere Module	In der Regel keine vorherige Registrierung der Studienleistung. Bescheinigungen über absolvierte Leistungen bitte dem Prüfungsamt Mathematik zur Verbuchung einreichen.
Prüfungsleistungen
Keine – aber alle bei der Verwendung der gewählten Veranstaltung in einem Studiengang des anbietenden Fachs vorgesehen Studien- wie Prüfungsleistungen sind als Studienleistungen zu absolvieren.
Bemerkungen
Für fachfremde Wahlmodule werden maximal 12 ECTS-Punkte auf die zu erreichenden 120 ECTS-Punkte angerechnet, es dürfen aber mehr Punkte absolviert werden. Module, die vollständig über dem Soll liegen, werden als Zusatzleistungen ausgewiesen.

Within the degree programme, you can choose the specialization in Financial Mathematics. It will prominently be mentioned on the examination documents. There is no specific application or registration for the specialization, however, proficiency in English of level B2 is expected. At the end of your studies, we will check whether all conditions are satisfied or not.

Further information and advice

• Dr. Ernst August Frhr. v. Hammerstein
  Ernst-Zermelo-Strasse 1, Room 248
  Phone +49 761 203-5673
  E-mail: ernst.august.hammerstein@stochastik.uni-freiburg.de

Profile line requirements

The curriculum of the normal master's degree programme applies with the following modifications:

(1) In the modules „Applied Mathematics“, „Mathematics“ and in the specialization module graded assessment must be obtained in at least three of the following areas:

• Stochastic processes
• Stochastic integration
• Financial mathematics
• Mathematical statistics

(2) The master's thesis must be written on a topic from financial mathematics.

(3) Instead of the elective modules, modules in economics amounting to at least 18 ECTS credits shall be taken. Admitted for this are those for the profile line Finance of the Master degree programme in Economics. Compulsory or elective modules. At least 6 ECTS points must be allocated to „special elective modules“; these are the courses scheduled for the second year of study.
The economics modules are offered in English; participation assumes sufficient knowledge of English (level at least B2).
Offered are e.g.:

• General and special compulsory modules:
  (annual) „Advanced Macroeconomics I“, „Advanced Macroeconomics II“, „Advanced Microeconomics I“, „Advanced Microeconomics II“, „Economic Policy and Public Choice“, „Computational Economics“, „Intermediate Econometrics“, „Principles of Finance“
• special elective modules:
  (annual) „Futures and Options“, Seminars and Topics courses from the field of „Finance“
  (irregular) „Computational Finance“, „Continuous Time Finance“, „Corporate Finance“, „Credit Risk“, „Financial Data Analysis“, „Interest Rate Theory“, „Portfolio Management“, „Risk Management“, „Time Series Analysis“

The compulsory and (special) elective modules in the finance profile of the M.Sc. Economics offered by the Institute of Economics in WS 2022/23 can be found in this table. Credit for the Financial Mathematics profile line is awarded for all courses except External Electives, if applicable.

Accordingly, the elective module is reduced to 0–3 ECTS points. The events for this can come from mathematics or other subjects.