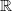 trop besteht aus den reellen Zahlen mit den Verknüpfungen
trop besteht aus den reellen Zahlen mit den Verknüpfungen
Seminar: | Tropische Geometrie |
Dozent: | Prof. Dr. B. Siebert |
Zeit/Ort: | Mo 14–16, SR 404, Eckerstr. 1 |
Tutorium: | Dr. Ursula Ludwig |
Vorbesprechung: | Do, 14.2., 13:15 Uhr, SR 404 Eckerstr. 1 |
Inhalt:
Der tropische Halbring 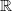 trop besteht aus den reellen Zahlen mit den Verknüpfungen
trop besteht aus den reellen Zahlen mit den Verknüpfungen
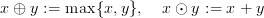
als Addition und Multiplikation. Es ist der Grenzfall t →∞ des Bildes des Halbrings
(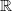 >0, +,⋅) unter dem Logarithmus zur Basis t.
>0, +,⋅) unter dem Logarithmus zur Basis t.
Tropische Geometrie ist Geometrie über 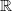 trop. Sie ist ein recht neues Gebiet mit Verbindungen
vor allem zur algebraischen Geometrie und zur Kombinatorik. So haben viele klassische Sätze
der algebraischen Geometrie tropische Entsprechungen, etwa der Satz von Bezout über die
Anzahl der Schnittpunkte ebener Kurven, die Adjunktionsformel über den topologischen Typ
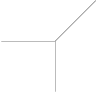
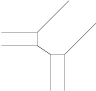
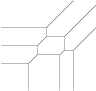
oder die Gruppenstruktur elliptischer Kurven. Die Bilder zeigen eine tropische Gerade, eine
tropische Quadrik und eine tropische Kubik.
trop. Sie ist ein recht neues Gebiet mit Verbindungen
vor allem zur algebraischen Geometrie und zur Kombinatorik. So haben viele klassische Sätze
der algebraischen Geometrie tropische Entsprechungen, etwa der Satz von Bezout über die
Anzahl der Schnittpunkte ebener Kurven, die Adjunktionsformel über den topologischen Typ
oder die Gruppenstruktur elliptischer Kurven. Die Bilder zeigen eine tropische Gerade, eine
tropische Quadrik und eine tropische Kubik.
Im Seminar werden wir Originalliteratur zu verschiedenen Aspekten der tropischen Geometrie studieren. Vorkenntnisse in algebraischer Geometrie sind nicht erforderlich, wenn auch bisweilen nützlich. Aus dem Seminar heraus können Themen für Staatsexams- und Diplomarbeiten vergeben werden.
Literatur:
Notwendige Vorkenntnisse: | Grundvorlesungen |
Nützliche Vorkenntnisse: | Algebraische Geometrie |
Sprechstunde Dozent: | Mi 13–14 |
Sprechstunde Assistentin: | Mi 14–15 |
Kommentar: | Interessenten mögen sich bitte in eine bei Frau Wöske, Zi. 336 (Mo–Mi 14–16.30, Do/Fr 9–12) ausliegende Liste eintragen. |