Viele der fundamentalen Erkenntnisse der Funktionentheorie beruhen unter anderem auf der Idee, holomorphe oder meromorphe Funktionen auf einem Gebiet G in der Riemannschen Zahlensphäre
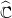als Abbildungen von G in ein weiteres Gebiet G′⊂
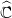zu
betrachten.Ziel dieses Seminars ist es, diesen geometrischen Ansatz weiter zu vertiefen, klassische Resultate der komplexen Analysis mit geometrischen Methoden zu beweisen und holomorphe Symmetrien von Gebieten zu studieren und zu verstehen.
Konkreter werden wir das Konzept einer Riemannschen Metrik auf Gebieten in
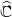einführen, das
es ermöglicht, in natürlicher Weise Abstände zwischen Punkten in G zu „messen“. Als eines der
ersten Resultate aus der Funktionentheorie wird dabei das Schwarzsche Lemma in neuem Licht
erscheinen, nämlich als eine Aussage über die Interaktion von holomorphen Funktionen auf der
Einheitskreisscheibe mit einer natürlichen Metrik. Anschließend werden wir mit Hilfe der neu
erarbeiteten Methoden einen geometrischen Beweis des Großen Satzes von Picard über das
Werteverhalten von holomorphen Funktionen in der Nähe einer essentiellen Singularität
geben.Ein weiterer Schwerpunkt des Seminars wird das Studium der Automorphismengruppen von Gebieten in
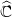mit Hilfe von invarianten Metriken sein. Hierbei werden wir zumindest heuristisch
und in Beispielen das Konzept der Riemannschen Fläche kennenlernen.Als Ausblick werden wir schließlich in einfachen Beispielen sehen, dass die Welt der mehrdimensionalen komplexen Analysis wesentlich vielfältiger ist, als man dies aus der reellen Theorie und der Theorie einer komplexen Variablen erwarten könnte.
Das unten angegebene Buch von Krantz vermittelt einen guten Eindruck von den im Seminar behandelten Themen, aus dem Buch von Katok sind die ersten drei Kapitel für das Seminar relevant.