∘ | 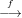 | ∘ |
1 | 2 |
Proseminar: | Köcher |
Dozentin: | Prof. Dr. Katrin Wendland |
Zeit/Ort: | Di, 14–16 Uhr, SR 125, Eckerstr. 1 |
Tutorium: | Magnus Engenhorst |
Vorbesprechung: | Mittwoch, 03.08.2011, 12:30 Uhr, SR 125, Eckerstr. 1 |
Web-Seite: | http://home.mathematik.uni-freiburg.de/mathphys/lehre/WiSe11/koecher.html |
Inhalt:
Diagramme sind nützlich, um komplizierte Zusammenhänge in der Mathematik zu erfassen. So bezeichnet die
Notation f:V 1-→V 2 bekanntlich eine Abbildung f von V 1 nach V 2, z.B. eine lineare Abbildung zwischen
Vektorräumen V 1 und V 2. Eine vereinfachte Form dieses Diagrammes ist ein sogenannter orientierter Graph
∘ | 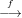 | ∘ |
1 | 2 |
∘ |
1 |
∘ |
2 |
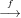 , also Pfeilen. Da Pfeil-Sammlungen traditionell in Köchern aufbewahrt werden,
hat sich der Begriff Köcher für diese orientierten Graphen eingebürgert. Um allerdings aus dem Köcher
, also Pfeilen. Da Pfeil-Sammlungen traditionell in Köchern aufbewahrt werden,
hat sich der Begriff Köcher für diese orientierten Graphen eingebürgert. Um allerdings aus dem Köcher
∘ |  | ∘ |
1 | 2 |
Wann sollen wir zwei Darstellungen eines gegebenen Köchers als unterschiedlich ansehen? Die natürliche Antwort verwendet das Isomorphiekonzept aus der linearen Algebra und die Verknüpfung linearer Abbildungen mit Isomorphismen. Wieviele unterschiedliche Darstellungen hat ein gegebener Köcher? Diese Frage ist je nach betrachtetem Köcher eine Umformulierungen oder eine natürliche Verallgemeinerung eines der üblichen Klassifikationsprobleme aus der linearen Algebra.
Die mathematische Theorie der Köcher verknüpft elegant Ideen aus der Kombinatorik, die man sich anhand der Köcher veranschaulichen kann, mit sehr konkreten Fragen aus der linearen Algebra und ihren Verallgemeinerungen. Es bestehen enge Zusammenhänge zu vielen aktiven Forschungsbereichen in der Mathematik, von der Darstellungstheorie sogenannter endlich-dimensionaler Algebren und Kac-Moody Lie-Algebren und bis hin zu den sogenannten Köcher-Eichtheorien in der theoretischen Physik. Im Proseminar sollen Grundlagen dieser Theorie anhand von Beispielen eingeführt werden. Einen schönen Übersichtsartikel aus den Notices of the Amercan Mathematical Society von H. Derksen und J. Weyman findet man unter folgender Internetadresse: http://www.ams.org/notices/200502/fea-weyman.pdf
Literatur:
Typisches Semester: | ab dem 3. Semester |
ECTS-Punkte: | 3 Punkte |
Sprechstunde Dozentin: | Di, 10–11 Uhr, Raum 337, Eckerstr. 1 |
Sprechstunde Assistent: | n.V., Raum 324, Eckerstr. 1 |