[next] [prev] [prev-tail] [tail] [up]

1.10 Variationsrechnung in einer Dimension

Vorlesung:

Variationsrechnung in einer Dimension

  

Dozentin:

Paola Pozzi, PhD

  

Zeit/Ort:

Do 14-16, SR 226 Hermann-Herder-Str. 10

  

Web-Seite:

http://aam.mathematik.uni-freiburg.de/IAM/homepages/paola/

  

Inhalt:

Das Ziel der Variationsrechnung ist es, optimale Lösungen eines Problems zu finden und ihre Eigenschaften zu beschreiben. Zum Beispiel kann man die kürzeste Verbindung zwischen zwei Punkten auf einer Fläche suchen. Die Variationsrechnung spielt in Geometrie, Physik und Numerik eine wichtige Rolle.

Thema der Vorlesung ist eine Einführung in die Variationsrechnung in einer Dimension. Technisch betrachtet etwas einfacher, beleuchtet der eindimensionale Fall zahlreiche Phänomene, die auch bei mehrdimensionalen Problemen eine Rolle spielen.

Hauptthema wird die Frage nach der Existenz und den Eigenschaften von Minima - oder allgemeiner von Extrema - von Funktionalen sein. Funktionale ordnen einer Funktion u = u(x), x ∈ (a,b) eine reelle Zahl

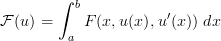
∫ b F (u) = F(x,u (x),u′(x ))dx a
zu. Hierbei ist die Funktion F gegeben und vom konkreten Problem abhängig.

Nach einer Einführung mit den klassichen Methoden, werden wir uns mit den moderneren sogenannten “direkten Methoden” vertraut machen.

Literatur:

  1. B. Dacorogna, Introduction to The calculus of Variations, Imperial College Press, 2004

Typisches Semester:

ab 5. Semester

Studienschwerpunkt:

Angewandte Mathematik, Analysis

Notwendige Vorkenntnisse:

Grundvorlesungen Analysis, Lineare Algebra

Sprechstunde Dozentin:

Do 16:15-17:15, R 213 Hermann-Herder-Str. 10

[next] [prev] [prev-tail] [front] [up]