Lehrveranstaltungen

Inhalt:
Die Funktionentheorie befasst sich mit Funktionen in einer komplexen Veränderlichen. Sie ist ein schönes und interessantes Teilgebiet der Mathematik, das sowohl in vielen Bereichen der Mathematik als auch beispielsweise in der Physik Anwendungen hat.

Komplex differenzierbare Funktionen f : U → ℂ auf einem Gebiet U ⊂ ℂ nennt man holomorph. Eine holomorphe Funktion erfüllt die Cauchy-Riemann-Differentialgleichungen und hat daher viele schöne Eigenschaften. Zum Beispiel ist jede holomorphe Funktion analytisch, das heißt, sie ist unendlich oft differenzierbar und wird lokal stets durch ihre Taylorreihe dargestellt. Eine holomorphe Funktion auf der abgeschlossenen Kreissscheibe wird bereits durch ihre Werte auf dem Rand vollständig bestimmt.

Wir lernen zunächst die Grundlagen der Funktionentheorie kennen wie den Cauchyschen Integralsatz, die Cauchysche Integralformel, das Maximumprinzip, den Satz von Liouville und den Residuensatz. Anschließend beschäftigen wir uns mit dem Riemannschen Abbildungssatz, und, sofern die Zeit es erlaubt, mit weiteren Themen.

Literatur:

1.)

E. Freitag, R. Busam, Funktionentheorie 1, Springer, Berlin, 1993

2.)

K. Jänich, Funktionentheorie, Springer-Verlag, Berlin, 1993

Weitere Literatur wird in der Vorlesung angegeben.__________________________________________________________

Inhalt:

In der Vorlesung soll eine Einführung in die Elementargeometrie im Euklidischen und nicht-Euklidischen Raum und seiner mathematischen Grundlagen gegeben werden. Wir behandeln im Einzelnen dazu die Themen der Axiomatik, Isometrien-Bewegungsgruppe und Trigonometrie der euklidischen, hyperbolischen und sphärischen Geometrie. Im weiteren Verlauf schauen wir uns die Geschichte des fünften Euklidischen Axioms (und die Versuche es los zu werden) an, diskutieren die kontraintuitiven Ergebnisse der daraus hervogegangen hyperbolischen Geometrie (z.B. existieren dort Dreiecke mit der Innenwinkelsumme gleich Null) und werden einem kurzen Exkurs in die spezielle Relativitätstheorie geben. Ferner geben wir eine Einführung in die Projektive Geometrie und betrachten Polygone, Polyeder und deren Eigenschaften.

Literatur:

1.)

C. Bär, Elementare Differentialgeometrie, Walter de Gruyter, 2010.

2.)

M. Berger, Geometry I, Universitext, Springer-Verlag, 2009.

3.)

R. Hartshorne, Geometry: Euclid and beyond, Springer, 2000.

4.)

H. Knörrer, Geometrie, Vieweg, 1996.

Inhalt:
Die Komplexe Geometrie verbindet zwei Gebiete in der Mathematik: Die Differentialgeometrie und die algebraische Geometrie. Sie kann als ein Spezialfall der klassischen Riemannschen Geometrie verstanden werden, in dem wesentliche neue Techniken zur Verfügung stehen, nämlich die der komplexen Funktionentheorie. Dies erlaubt interessante Anwendungen, z.B. im Zusammenhang mit sogenannten Calabi-Yau-Mannigfaltigkeiten, die in der modernen theoretischen Physik eine wesentliche Rolle spielen.

Ziel der Vorlesung ist es, die wichtigsten und grundlegenden Techniken zum Studium solcher komplexer Mannigfaltigkeiten zu lehren und einige Beispielklassen sowie Anwendungen zu diskutieren. Insbesondere werden wir sogenannte Kähler-Mannigfaltigkeiten und ihre besonderen Eigenschaften studieren, d.h. Mannigfaltigkeiten, deren Riemannsche Metrik eng mit der komplexen Struktur verworben ist. Die für die theoretische Physik relevanten Beispielklassen werden ausführlich behandelt, nämlich die erwähnten Calabi-Yau-Mannigfaltigkeiten, und unter diesen insbesondere die sogenannten K3-Flächen.

Es werden Grundkenntnisse aus der Differentialgeometrie sowie Funktionentheorie vorausgesetzt; aus der algebraischen Geometrie wird kein Vorwissen vorausgesetzt.

Literatur:

1.)

Daniel Huybrechts, “Complex Geometry”, (Springer 2005)

2.)

R.O. Wells, “Differential Analysis on Complex Manifolds”, (Springer 1986)

3.)

W.P. Barth, K. Hulek, Ch.A.M. Peters, A. van de Ven, “Compact Complex Surfaces”, (Springer 2004), Kapitel VIII

Inhalt:
Die Funktionalanalysis verallgemeinert Methoden und Begriffe aus der Analysis und der linearen Algebra auf unendlich–dimensionale Vektorräume, auf denen ein Konvergenzbegriff gegeben ist (z.B. eine Norm oder eine Metrik). Insbesondere werden Abbildungen zwischen solchen Räumen untersucht. Besonders angestrebt werden Ergebnisse, die sich auf konkrete Funktionenräume (z.B. L²(Ω),C(Ω)) anwenden lassen. In der Vorlesung werden die notwendigen Grundlagen detailliert behandelt und an konkreten Problemen illustriert.

Literatur:

1.)

H. Brezis: Functional Analysis, Sobolev Spaces and Partial Differential Equations, Springer 2011

2.)

J. Conway: A course in functional analysis, Springer 2007

Inhalt:
Man kann „Kommutative Algebra“ auf zwei sehr verschiedene Arten motivieren.

Algebraisch: Es geht um praktisch beliebige kommutative Ringe und ihre “Moduln”. Die Lineare Algebra wird ein Spezialfall: In ihr ist der Ring immer ein Körper k und dann betrachtet man Vektorräume über k. Mit ähnlichen Axiomen kann man nun k durch einen beliebigen kommutativen Ring R ersetzen und das Analogon eines Vektorraums, den man dann „R-Modul“ nennt, untersuchen. Die Theorie wird viel reichhaltiger.

Geometrisch: Viele geometrische Gebilde lassen sich durch Polynomgleichungen in mehreren Variablen definieren. Ein Beispiel: Alle Punkte (x,y) eines Kreises vom Radius 1 haben den Abstand 1 zum Mittelpunkt. In Gleichungen: Das sind genau die Paare (x,y) ∈ ℝ², die

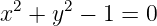
erfüllen - eine Polynomgleichung in zwei Variablen. Man kann sich nun überlegen, dass die auf einem Kreis definierten polynomialen Funktionen gerade den Elementen aus dem Ring

entsprechen. Man kann nun zeigen, dass sich viele geometrische Eigenschaften des Kreises in algebraischen Eigenschaften des Rings R widerspiegeln. Nun ist R aber ein kommutativer Ring, d.h. wir sind wiederum beim Studium kommutativer Ringe. Dies funktioniert nicht nur für den Kreis, sondern für alle geometrischen Objekte, die durch polynomiale Gleichungen definierbar sind. Dieses Wechselspiel von Algebra und Geometrie macht den Reiz der Disziplin aus. Zahlreiche der in den letzten Jahrzehnten vergebenen Fields-Medaillen waren für bahnbrechende Arbeiten im Bereich der Algebraischen Geometrie, z.B. Birkar, Scholze, Voevodsky, Faltings, etc.

Literatur:

1.)

Atiyah, MacDonald, Introduction to Commutative Algebra

2.)

Mumford, The red book of varieties and schemes

Inhalt:
Dieser einführende Kurs in die mathematische Logik besteht aus mehreren Teilen. Es werden die Grundlagen der Prädikatenlogik und eine kurze Einleitung in die Modelltheorie, sowie das Axiomensystem der Mengenlehre behandelt. Das Ziel der Vorlesung ist es, den rekursionstheoretischen Gehalt des Prädikatenkalküls, insbesondere die sogenannte Peano-Arithmetik und die Gödelschen Unvollständigkeitssätze, zu verstehen.

Literatur:

1.)

H.-D. Ebbinghaus, J. Flum, W. Thomas, Einführung in die mathematische Logik, Spektrum Verlag, 2007.

2.)

J.-R. Shoenfield, Mathematical Logic, Addison-Wesley, 2001.

3.)

M. Ziegler, Mathematische Logik, Birkhäuser, 2010.

4.)

A. Martin-Pizarro, Logik für Studierende der Informatik, Kurzskript, 2017,
http://home.mathematik.uni-freiburg.de/loesch/lehre/ws1819/Logik_Info.pdf

Inhalt:
Die Frage, wie eine vorgegebene diskrete Gruppe durch Automorphismen auf einem vorgegebenen Vektorraum operieren kann, führt über die Betrachtung des sogenannten Gruppenrings zur Frage nach der Struktur allgemeiner, nicht notwendig kommutativer Ringe. Wir gelangen darüber zur Charaktertheorie endlicher Gruppen und studieren sie insbesondere im Fall der symmetrischen Gruppen. Die Frage, wie eine vorgegebene kontinuierliche Gruppe durch Automorphismen auf einem vorgegebenen Vektorraum operieren kann, führt zur Theorie der Lie-Algebren und ihrer Darstellungen. Sie soll dann im weiteren Verlauf der Vorlesung besprochen werden.

Die Vorlesung benötigt kaum Voraussetzungen, die über den Stoff der Grundvorlesungen hinausgehen. Kenntnisse aus der Vorlesung Algebra und Zahlentheorie sind hilfreich, insbesondere der Begriff eines Ideals und der Begriff des Restklassenrings nach einem Ideal.

Literatur:

1.)

Jantzen-Schwermer, Algebra, Springer, 2014

2.)

Soergel, Nichtkommutative Algebra und Symmetrie, Skript

Inhalt:

In dieser Vorlesung untersuchen wir lineare elliptische partielle Differentialgleichungen:

∙ die harmonischen Funktionen

∙ die Poisson-Gleichungen

∙ das Maximum-Prinzip

∙ die Schauder-Theorie

∙ die Krylov-Safonov-Theorie

∙ die Moser-Theorie

Literatur:

1.)

Evans, Lawrence C.: Partial differential equations, Graduate Studies in Mathematics. 19, Providence, RI: American Mathematical Society (AMS) (1998)

2.)

Han, Qing: An Introduction to Elliptic Differential Equations, manuscript

3.)

Jost, Jürgen: Partielle Differentialgleichungen, Springer (1998)

Inhalt:
Diese Vorlesung schließt an die Stochastischen Prozesse aus dem WS 2018/19 an. Ausgehend von den dort bereits eingehender behandelten zeitstetigen Prozessen wird das stochastische Integral bezüglich der Brownschen Bewegung und allgemeinerer Klassen von Prozessen eingeführt und darauf aufbauend die Itô-Formel, stochastische Differentialgleichungen, Maßwechsel und die Girsanov-Transformation behandelt.

Als finanzmathematische Anwendungen werden insbesondere die Optionspreistheorie im Black-Scholes- und in allgemeineren Lévy-Modellen sowie einfachere Zinsmodelle betrachtet. Sofern Zeit bleibt, kann auch noch ein (kleiner) Einblick in die Fundamentalsätze der Preistheorie gegeben werden.

Literatur:

1.)

Cont, R., Tankov, P.: Financial Modelling with Jump Processes, Chapman & Hall, 2004

2.)

Irle, A.: Finanzmathematik, 3. Aufl., Springer, 2012

3.)

Jacod, J., Shiryeav, A.: Limit Theorems for Stochastic Processes, 2. Aufl., Springer, 2003

4.)

Kallenberg, O.: Foundations of Modern Probability, Springer, 2002

5.)

Klenke, A.: Wahrscheinlichkeitstheorie, 3. Aufl., Springer Spektrum, 2013

6.)

Protter, P.: Stochastic Integration and Differential Equations, 2. Aufl., Springer, 2005

Inhalt:
Ein topologischer Raum besteht aus einer Grundmenge X und einer Festlegung der Menge der offenen Teilmengen der Grundmenge, die Topologie auf X genannt wird. Beispiele über den Grundmengen ℝ und ℝⁿ kommen in den Analysis-Vorlesungen vor. Das mathematische Fach „Topologie“ ist die Lehre über topologische Räume und die Erforschung ebendieser. Unsere Vorlesung ist eine Einführung in die mengentheoretische und in die algebraische Topologie.

Literatur:

1.)

Ryszard Engelking, General Topology, Warschau 1977

2.)

Marvin Greenberg, Lectures on Algebraic Topology, Amsterdam 1967

3.)

Allen Hatcher, Algebraic Topology, Cambridge 2002

4.)

Klaus Jänich, Topologie, Spinger, 8. Auflage 2005

5.)

John Kelley, General Topology, New York 1969

6.)

Casimir Kuratowski, Topologie, Warschau 1958

7.)

James Munkres, Elements of Algebraic Topology, Cambridge, Massachesetts 1984

8.)

Boto von Querenburg, Mengentheoretische Topologie, Springer, 3. Auflage 2001

Inhalt:
The course’s aim is to give an introduction into numerical methods for the solution of optimal control problems in science and engineering. The focus is on both discrete time and continuous time optimal control in continuous state spaces. It is intended for a mixed audience of students from mathematics, engineering and computer science.

The course covers the following topics: Introduction to Dynamic Systems and Optimization

• Rehearsal of Numerical Optimization
• Rehearsal of Parameter Estimation
• Discrete Time Optimal Control
• Dynamic Programming
• Continuous Time Optimal Control
• Numerical Simulation Methods
• Hamilton–Jacobi–Bellmann Equation
• Pontryagin and the Indirect Approach
• Direct Optimal Control
• Differential Algebraic Equations
• Periodic Optimal Control
• Real-Time Optimization for Model Predictive Control.

The lecture is accompanied by intensive weekly computer exercises based on MATLAB (6 ECTS) and an optional project (3 ECTS). The project consists in the formulation and implementation of a self-chosen optimal control problem and numerical solution method, resulting in documented computer code, a project report, and a public presentation.

Literatur:

1.)

Manuscript Numerical Optimal Control by M. Diehl and S. Gros

2.)

Biegler, L. T., Nonlinear Programming, SIAM, 2010

3.)

Betts, J., Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, SIAM, 2010

Inhalt:
Die Risikotheorie ist die mathematische Theorie hinter der Schadenversicherungsmathematik, einem Zweig der Versicherungsmathematik. Während bei Lebensversicherungen nur der Leistungszeitpunkt zufällig ist, ist bei Schadenversicherungen neben dem Schadenzeitpunkt vor allem auch die Schadenhöhe zufällig und als schwer prognostizierbar anzusehen.

Die geplante Vorlesung knüpft nahtlos an die Vorlesung Versicherungsmathematik aus dem Wintersemester 2018/19 an, in der wir uns mit Lebensversicherungsmathematik beschäftigt haben, und in der wir bereits statische Modelle aus der Schadenversicherungsmathematik kennengelernt haben. Der Theorie stochastischer Prozesse wird nun eine noch größere Bedeutung als im letzten Semester zufallen.

Es sind unter anderem folgende Themen vorgesehen:

• Dynamische Modelle, Ruintheorie
• Prämienberechnung und Risikomaße
• Risikoverteilung, Rückversicherung
• Vergleich von Risiken

Literatur:

1.)

S. Asmussen, H. Albrecher: Ruin Probabilities. World Scientific, 2010

2.)

P. Embrechts, C. Klüppelberg, T. Mikosch: Modelling Extremal Events. Springer, 1997

3.)

H.W. Goelden, K.T. Hess, M. Morlock, K.D. Schmidt, K.J. Schröter: Schadenversicherungsmathematik. Springer, 2016

4.)

T. Mikosch: Non-life Insurance Mathematics. Springer, 2010

5.)

K.D. Schmidt: Versicherungsmathematik. Springer, 2006

Inhalt:
Finite simple groups are the building blocks of finite groups. In the abelian case these are precisely the cyclic groups. In the non-abelian case, classical examples include alternating groups, as well as certain matrix groups such as the projective special linear group over a finite field.

The classification of finite simple groups is far beyond the scope of this course, since it consists of tens of thousands of pages. Nevertheless, during this course we will illustrate some of the recurrent ideas of the classification. In particular, we will prove the following result of Brauer and Fowler:

Theorem. Let G be a finite simple non-abelian group of even order and let t be an element of order 2. Then |G|≤ (|C_G(t)|²)!.

In words of Solomon, the Brauer–Fowler Theorem had a particularly great psychological impact and in fact, it suggested that finite simple groups could be classified by studying centralizers of elements of order two.

Literatur:

1.)

J. S. Rose, A course on Group Theory, Cambridge University Press, 1978

2.)

J. J. Rotman, An introduction to the Theory of Groups, Springer-Verlag, 1999

3.)

R. Solomon, A brief history of the classification of the finite simple groups, Bulletin American Mathematical Society 38 (2001), no. 3, 315–352

Inhalt:
The aim of the course is to focus on games with two players and infinite moves. Such types of games have been well-studied along the years in a branch of mathematical logic called descriptive set theory. Along the lecture we are going to focus on the set theoretical aspects of infinite games, studying the interplay with topological and measure-theoretical questions; more specifically we focus on Banach-Mazur game, the perfect set game and some other variants. Moreover, we also present connections with social choice theory and social welfare theory, such as Arrow’s impossibility theorem and the analysis of Pareto pre-orders and/or other principles coming from theoretical economics like Hammond equity and finite anonymity.

Literatur:

1.)

A.S. Kechris, Classical Descriptive Set Theory, Springer, 1995

2.)

A. Kanamori, The Higher Infinite, Springer, 1994

3.)

T. Jech, Set Theory, Springer, 3rd Milleniuum edition, 2003

Inhalt:
This course provides an introduction to the theory of parabolic partial differential equations. Such equations arise in many applications, such as heat conduction and other physical and biological models.

The following topics will cover the major part of the lecture.

1.

The one- and multidimensional heat equation, fundamental solution, elementary methods and representation formulas.

2.

Maximum principles for general linear parabolic equations.

3.

Weak solutions and Galerkin-Method

4.

If time permits, we will discuss some semi-group approaches.

5.

We will keep having an eye on applications, such as random walks and models from finance.

The content is disjoint from the content of the course ‘Partielle Differentialgleichungen’ by Prof. Wang and could well be attended complementary. The presentation will be at a basic level and technicalities are kept to a minimum.

Literatur:

1.)

Lawrence C. Evans, Partial differential equations, AMS, Graduate studies in mathematics 19

2.)

Sandro Salsa, Partial Differential Equations in Action, Springer Universitext, 2008.

3.)

Walter Strauss, Partial Differential Equations, John Wiley & Sons, 1992.

Inhalt:
In dieser Vorlesung werden wir den mathematischen Modellierungsprozess an mehreren Beispielen demonstrieren. Am Anfang steht jeweils eine Frage aus den Anwendungen wie z.B. Physik, Biologie, Chemie oder Wirtschaft. Durch Definition geeigneter Größen wird diese Frage dann in die Sprache der Mathematik übersetzt, z.B. in eine Gleichung, gewöhnliche Differentialgleichung oder auch eine partielle Differentialgleichung. In der Vorlesung werden wir Beispiele zu den Themen Wärmeleitung, Diffusion, Schwingungen von Stäben und Membranen, Strömungen von reibungsfreien und reibunsbehafteten Strömungen, Kapillarität, Populationsdynamik, Elastizität und Verkehrssimulation besprechen.

Literatur:

1.)

C. Eck et al., Mathematische Modellierung, Springer 2017.

2.)

A. Jüngel, Mathematische Modellierung mit Differentialgleichungen, unkorrigiertes Vorlesungsskript 2003.

3.)

M. Burger, Mathematische Modellierung, Vorlesungsskript, Münster 2006.
http://www.math.uni-muenster.de/u/burger/

4.)

J. Gerstenberger, R. Klöfkorn, D. Kröner, T. Malkmus, D. Nies, M. Nolte, A. Pfeiffer, T. Strauch, H. Thorburn, Transport Vulkanasche: Eine interaktive Simulation.
https://imaginary.org/de/program/dune-ash

5.)

D. Helbing, Traffic and related self-driven many particle systems, Rev. Mod. Phys. 73(2001) p. 1067.

6.)

C.P. Ortlieb, C.v. Dresky, I. Gasser, S. Günzel, Mathematische Modellierung. Eine Einführung in zwölf Fallstudien, Springer, Wiesbaden 2013.

7.)

S. Rahmstorf, A simple model of seasonal open ocean convection, Part I: Theory, Ocean Dynamics 52 (2001), 26–35.

8.)

www.traffic-simulation.de/onramp.html

Inhalt:
Gewöhnliche Differentialgleichgungen sind Gleichungen für Funktionen und deren Ableitungen, die nur von einer reellen Variablen abhängen. Diese dienen als mathematisches Modell z.B. für die Berechnung von Flugbahnen, Evolutionsprozessen (Anfangswertprobleme) oder die Verbiegung von eindimensionalen Balken (Randwertproblem). In der Vorlesung werden numerische Algorithmen entwickelt und analysiert um Anfangswert- oder Randwertprobleme zu lösen.

Literatur:

1.)

S. Bartels: Numerik 3x9. Springer 2016

2.)

R. Plato: Numerische Mathematik kompakt. Vieweg 2000

3.)

W. Walter: Gewöhnliche Differentialgleichungen: Eine Einführung. Springer 2000

Inhalt:
Die Rekursionstheorie ist die Theorie der berechenbaren Funktionen. Sie gehört neben der Beweistheorie, der Mengenlehre und der Modelltheorie zu den wichtigsten Teilgebieten der mathematischen Logik.

Neben der unten angegebenen Literatur empfehle ich die Kapitel über Rekursiontheorie in Shoenfield Mathematical Logic und Ziegler Mathematische Logik.

Literatur:

1.)

Barry Cooper, Computability Theory, Chapman and Hall 2004

2.)

Nigel Cutland, Computability, Cambridge 1980

3.)

Hartley Rogers Jr., Theory of Recursive Functions and Effective Computability, McCraw-Hill, New York 1967

4.)

Robert Soare, Recursively Enumerable Sets and Degrees, Springer 1987

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich (im Zwei-Hauptfächer-Bachelor: „Optionsbereich“) angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Leistungsnachweis:

• Teilnahme an dem neu konzipierten Einführungsworkshop. Voraussichtlich etwa zwei halbe Tage; einen ungefähr in der ersten Vorlesungswoche und einen nach etwa vier Wochen. Näheres wird rechtzeitig bekanntgegeben.
• regelmäßige Teilnahme an der Tutorenbesprechung;
• zwei gegenseitige Tutoratsbesuche mit einem (oder mehreren) anderen Modulteilnehmer, welcher nach Möglichkeit die gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten, und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der Einführungsveranstaltung).

In Ermangelung eines passenden Wahlbereichs kann das Modul im Lehramtsstudiengang in dieser Form leider nicht angeboten werden. Im 2-Hauptfächer-Bachelor ist es bei Wahl der Lehramtsoption eine über die 180 geforderter ECTS-Punkte hinausgehende Zusatzleistung.__________________________________________________________________________________________________

Inhalt:
Als Schüler ahnt man nicht, was es heißt, Mathematik zu studieren. Ähnlich vage ist häufig die Vorstellung im Studium davon, was es bedeutet, Mathematik in der Schule zu unterrichten. Dieses Seminar möchte konkrete Aus- bzw. Einblicke in die Praxis des Mathematikunterrichtens geben und versucht dabei, auf den Erfahrungen z.B. aus dem Praxissemester aufzubauen.

Ausgewählte Inhalte und Aspekte des Mathematikunterrichts (vom Arbeitsblatt bis zur Zahlenbereichserweiterung) werden nicht nur vom Standpunkt der Fachwissenschaft, sondern auch aus Lehrer- und Schülersicht analysiert und hinterfragt. Oft verbergen sich hinter den mathematisch einfacheren Themen unerwartete didaktische Herausforderungen. Daher soll neben der Auseinandersetzung mit bestehenden Inhalten und Rahmenbedingungen auch Unterricht selbst geplant und – wenn möglich – an der Schule durchgeführt werden.______________________

Inhalt:
In diesem Praktikum werden die in der Vorlesung „Mathematische Modellierung“ besprochenen Probleme implementiert, um numerische Näherungslösungen zu berechnen und zu visualisieren. Grundlage für die Programmierung sind die Programmiersprache C, C++ und MATLAB.

Literatur:

1.)

S. Bartels: Numerik 3x9. Springer 2016

Inhalt:
In der praktischen Übung zur Numerik-Vorlesung werden die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet. Dies wird mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

S. Bartels: Numerik 3x9. Springer, 2016.

2.)

R. Plato: Numerische Mathematik kompakt. Vieweg, 2006.

3.)

R. Schaback, H. Wendland: Numerische Mathematik. Springer, 2004.

4.)

J. Stoer, R. Burlisch: Numerische Mathematik I, II. Springer, 2007, 2005.

5.)

G. Hämmerlin, K.-H. Hoffmann: Numerische Mathematik. Springer, 1990.

6.)

P. Deuflhard, A. Hohmann, F. Bornemann: Numerische Mathematik I, II. DeGruyter, 2003.

Inhalt:
In diesem Praktikum werden die in der Vorlesung ”Numerik für Differentialgleichungen” besprochenen Algorithmen implementiert, um numerische Näherungslösungen für Anfangs-und Randwertprobleme zu berechnen und zu visualisieren. Grundlage für die Programmierung sind die Programmiersprache C, C++ und MATLAB.

Literatur:

1.)

S. Bartels: Numerik 3x9. Springer 2016

Inhalt:
Die praktische Übung richtet sich an Hörerinnen und Hörer der Vorlesung Stochastik. Es werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der Vorlesung vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird das frei verfügbare Open-Source-Statistikprogramm R verwendet werden. Nach einer Einführung in R werden u.a. Verfahren der deskriptiven Statistik und graphischen Auswertung von Daten betrachtet, die numerische Erzeugung von Zufallszahlen erläutert sowie parametrische und nichtparametrische Tests und lineare Regressionsverfahren diskutiert. Vorkenntnisse in R und/oder Programmierkenntnisse werden dabei nicht vorausgesetzt.

Die praktische Übung ist für Studierende im (1-Hauptfach) B.Sc. Mathematik obligatorisch. Studierende des 2-Hauptfächer-Bachelors mit Lehramtsoption können selbstverständlich ebenfalls teilnehmen und die praktische Übung als Teil des Wahlpflichtmoduls Mathematik im Rahmen ihres Studiengangs verbuchen. Im Studiengang Master of Education kann die Veranstaltung als Mathematische Ergänzung belegt werden.

Für die eigene Arbeit mit R sollen die Laptops der Studierenden eingesetzt werden. Idealerweise sollte auf diesen bereits vor Beginn der Veranstaltung die dazu notwendige Software installiert werden. Genauere Anleitungen hierzu sowie entsprechende Links zum Download der kostenlosen Programme werden frühzeitig auf der o.g. Webseite bekannt gegeben.

Zu den einzelnen Lektionen der praktischen Übung wird ein ausführliches Skriptum bereitgestellt werden. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher zu R empfohlen werden.______________________________________________________________________________________

Inhalt:
 
Im täglichen Leben hilft die Mathematik, Probleme aus verschiedensten Bereichen zu beschreiben, zu verstehen und zu lösen. Das beginnt bei Fragen, wie der Taschenrechner den Sinus eines Winkels berechnet und ist die Basis für viele moderne technische Errungenschaften des modernen Lebens von Datenverarbeitung, Kommunikation und Lokalisationsaufgaben.

In den Vorträgen soll es darum gehen, einzelne Anwendungen zunächst vorzustellen, das zugrundeliegende mathematische Problem herauszuarbeiten und dann seine Lösung zu präsentieren. Die angegebene Literatur dient dabei nur als erster Anhaltspunkt, weitere Quellen sollen die Teilnehmerinnen und Teilnehmer selbst finden.

Eigene Themenvorschäge der Teilnehmerinnen und Teilnehmer sind willkommen, sofern sie in den Rahmen des Proseminars passen. In diesem Fall bitten wir, rechtzeitig vor der Vorbesprechung mit uns Kontakt aufzunehmen._______________________________________________________

Inhalt:
Im Proseminar werden wir uns grundlegende Eigenschaften von Funktionenräumen ansehen. Die betrachteten Räume verallgemeinern die Lebesgueräume L^p(Ω). Der gewählte Zugang benötigt keine Vorkenntnisse aus der Funktionalanalysis.

Literatur:

1.)

L. Pick, A. Kufner, O. John, S. Fučik: Function spaces Vol.1, De Gruyter 2013

Inhalt:
Die Vervollständigung der rationalen Zahlen bezüglich des üblichen Absolutbetrags führt zum Körper der reellen Zahlen. Auf ℚ lassen sich aber auch andere Absolutbeträge definieren, zum Beispiel die sogenannten p-adischen Absolutbeträge mit einer Primzahl p. Vervollständigt man die rationalen Zahlen bezüglich eines solchen p-adischen Absolutbetrags, dann erhält man einen Körper, der ganz andere topologische Eigenschaften aufweist als ℝ. Hiervon ausgehend werden wir viele Konzepte der Analysis, wie zum Beispiel das der Konvergenz, nochmals entwickeln und mit den bekannten vergleichen – mit vielen überraschenden Ergebnissen. So konvergieren Reihen genau dann im p-adischen Sinne, wenn ihre Summanden eine Nullfolge bilden, die Exponentialreihe hat einen endlichen Konvergenzradius, jeder innere Punkt eines Kreises ist dessen Mittelpunkt und vieles weitere ...

Dieses Proseminar eignet sich besonders für Studierende des zweiten Semesters, da die Konzepte der Analysis I Verwendung finden beziehungsweise sogar neu erarbeitet werden. Damit entsteht insbesondere auch ein tiefergehendes Verständnis der klassischen Analysis.

Literatur:

1.)

Fernando Gouvea, p-adic Numbers – An Introduction, Springer-Verlag

2.)

Neal Koblitz, p-adic Numbers, p-adic Analysis and Zeta-Functions, Second Edition, GTM 58

Inhalt:
One of the oldest avenues of research in algebraic geometry is enumerative geometry, whose aim is to compute the number of objects satisfying certain geometric conditions. One beautiful example of an enumerative problem is that of determining the number N_d of rational curves of degree d passing through 3d - 1 points in the projective plane ℙ². The numbers N ₁ = N₂ = 1 were known already from antiquity, while N₃ = 12 was computed in 1848 by Steiner, albeit with methods that lacked a rigorous foundation. Despite the advances in intersection and deformation theory in the 20th century, which resulted in many classical enumerative problems being solved, the determination of the numbers N_d proved to be more difficult than expected. The turning point came in the 90s, when a connection between enumerative geometry and string theory was discovered. The breakthrough was the realisation that the counts of various enumerative problems can be organised in terms of certain physical quantities (correlation functions of some topological quantum field theories) and computed using the product rules of a deformation of the de Rham cohomology, namely quantum cohomology.

The purpose of the seminar is to understand the derivation via quantum cohomology of the Kontsevich formula that yields the numbers N_d for an arbitrary d. In doing so, we shall introduce the concept of moduli spaces in algebraic geometry and discuss some basics of deformation theory (which will explain why 3d - 1 is the appropriate number of points to consider). We shall then reformulate the problem in terms of moduli spaces of stable maps to ℙ², define Gromov-Witten invariants, and set up the necessary axiomatics of topological quantum field theories and quantum cohomology.

Literatur:

1.)

J. Kock, I. Vainsencher, An invitation to quantum cohomology, Birkäuser, 2007

2.)

S. Katz, Enumerative geometry and string theory, American Mathematical Society, 2006

3.)

W. Fulton, R. Pandharipande, Notes on stable maps and quantum cohomology, arXiv:alg-geom/9608011

Inhalt:
Nichtlineare Wahrscheinlichkeiten sind ein top-aktuelles Thema in der angewandten Stochastik – wenn zum Beispiel ein Modell nicht exakt spezifiziert werden kann, und man Modellrisiken einschließen möchte, kann man das klassische Wahrscheinlichkeitsmaß P durch ein supremum über Wahrscheinlichkeitsmaße die als Modelle in Frage kommen ersetzen und erhält eine ähnliche Theorie wie die klassische Theorie von A. Kolmogorov, mit einigen entscheidenden Änderungen.

In diesem Seminar möchten wir diesen neuartigen Ansätzen auf den Grund gehen und einige grundlegende Arbeiten sowie Anwendungen in der Finanzmathematik kennenlernen.

Literatur und weitere Informationen finden Sie auf der Homepage.______________________________

Inhalt:
Kalibrierte Geometrie ist eine effektive Methode, um minimale Untermannigfaltigkeiten im Euklidischen Raum oder in Riemannschen Mannigfaltigkeiten aufzuspüren. Beispielsweise sind alle projektiven Varietäten im ℂPⁿ mit der Fubini-Study-Metrik durch Potenzen der Kähler-Form kalibriert und daher minimal. Umgekehrt kann die Existenz kalibrierter Untermannigfaltigkeiten in einer Riemannschen Mannigfaltigkeit M viel über die Geometrie von M aussagen.

Im ersten Teil des Seminars führen wir Kalibrierungen auf dem ℝⁿ ein und diskutieren zugehörige kalibrierte Untermannigfaltigkeiten, siehe [1] und [2].

Anschließend führen wir bestimmte Mannigfaltigkeiten spezieller Holonomie ein und betrachten ihre Kalibrierungen [3]. Dabei interessieren wir uns auch dafür, ob solche kalibrierten Untermannigfaltigkeiten eindeutig sind, oder aber in Familien auftreten [4].

Der genaue Inhalt des Seminars richtet sich nach den Interessen und Vorkenntnissen der Teilnehmerinnen und Teilnehmer. Nehmen Sie bei Interesse daher gern Kontakt mit einer/einem von uns auf.

Literatur:

1.)

R. Harvey, Spinors and calibrations, Academic Press, Boston, 1990

2.)

R. Harvey, H. B. Lawson, Calibrated geometries, Acta Math. 148 (1982), 47–157

3.)

D. Joyce, Riemannian holonomy groups and calibrated geometry, Oxford University Press, Oxford, 2007

4.)

R. McLean, Deformations of calibrated submanifolds, Comm. Anal. Geom. 6 (1998), 705–747

Inhalt:
 
Variationsrechnung ist eines der ältesten Teilgebiete der Analysis. In der Variationsrechnung geht es darum, Extremstellen von Funktionalen zu finden. Viele Fragestellungen aus der Geometrie (Geodätische, d.h. kürzeste Verbindungen zwischen zwei Punkten; Minimalflächen), den partiellen Differentialgleichungen und der Physik (klassische Mechanik, Optik und Feldtheorie) führen auf unendlichdimensionale Extremwertaufgaben. In dem Seminar werden die direkte Methode sowie die Minimax-Methode untersucht.

Literatur:

1.)

Struwe, Variational methods. Third edition. Ergebnisse der Mathematik und ihrer Grenzgebiete, 4. Folge, A Series of Modern Surveys in Mathematics, 34, Springer-Verlag, Berlin, 2008

Inhalt:
Viele Phänomene in der Natur lassen sich durch mathematische Modelle, insbesondere durch partielle Differentialgleichungen, beschreiben. Die wichtigsten unter diesen sind die elliptischen, die parabolischen und die hyperbolischen Differentialgleichungen. Gesucht werden jeweils Funktionen mehrerer Veränderlicher, deren Ableitungen gewisse Gleichungen erfüllen. Eine besondere Klasse von partiellen Differentialgleichungen bilden die hyperbolischen Erhaltungssätze. Trotz beliebig glatter Daten (damit sind Randwerte, Anfangswerte, Quellterme und die Koeffizienten gemeint), können die zugehörigen Lösungen unstetig sein. Daher ist ihre Behandlung eine besondere Herausforderung an die Analysis und die Numerik. Diese Differentialgleichungen sind mathematische Modelle für Strömungen kompressibler Gase und für verschiedene Probleme aus den Bereichen Astrophysik, Grundwasserströmungen, Meteorologie, Halbleitertechnik und reaktive Strömungen. Es ist das Ziel des Seminars, die theoretischen Grundlagen wie Existenz und Eindeutigkeit von Lösungen, zu zeigen und die Entwicklung und Analyse von numerischen Algorithmen.

Literatur:

1.)

M. Feistauer, J. Felcman, I. Straskraba, Mathematical and computational methods for compressible flow, Oxford Science Publications 2003.

2.)

D. Kröner, Numerical schemes for conservation laws, Wiley und Teubner 1997.

3.)

R. LeVeque, Numerical methods for conservation laws, Birkhäuser Verlag 1992.

Inhalt:
 
In dem Seminar geht es zunächst um Fourierreihen periodischer Funktionen und ihre Anwendungen. Für nichtperiodische Probleme wird die Theorie der Fouriertransfomation auf ℝ und ℝⁿ eingeführt und auf Beispiele angewendet

Literatur:

1.)

Stein, Shakarchi; Fourier Analysis: an Introduction, Princeton Universtity Press, 2003

Inhalt:
The real numbers form a completion of the rational numbers, and other completions are given by the so-called p-adic numbers. These are the first examples of local fields. Local fields are a very important concept in the study of number fields (finite extensions of ℚ), because they allow us to study problems “locally”. For example, one of the main goals in number theory is to study solutions of polynomial equations over the integers or the rationals. This is a very hard problem, but one can make some progress by studying the solutions locally over the p-adic numbers for every prime p. In this seminar we will follow the book “Local Fields” by Serre, and explore the basic properties of local fields. The goals of this seminar are a proof of the local Kronecker–Weber theorem and the statement of local class field theory. At the end of this seminar, students should be well prepared to study the proof of (local) class field theory, one of the highlights of number theory in the previous century.

Literatur:

1.)

Serre, Jean-Pierre. Local fields. Translated from the French by Marvin Jay Greenberg. Graduate Texts in Mathematics, 67. Springer-Verlag, New York-Berlin, 1979. viii+241 pp. ISBN: 0-387-90424-7

2.)

Neukirch, Jürgen. Algebraische Zahlentheorie. Springer-Verlag, Berlin, 1992. xiii+595 pp. ISBN: 3-540-54273-6

Inhalt:
Aufbauend auf der Vorlesung Wahrscheinlichkeitstheorie werden in dieser Veranstaltungen Themen für eine erste Abschlussarbeit in Mathematik (Bachelor oder Zulassungsarbeit) vorgestellt. Die Themen können sowohl direkt an die Vorlesung Wahrscheinlichkeitstheorie anschließen als auch Anwendungen enthalten, z.B. aus den Themenbereichen Finanzmathematik, Statistik oder Biologie._______________________________________________________________________________________

Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik dienen.

Vorbesprechung mit Hinweisen auf einführende Literatur:
Mittwoch den 06.02.2019, 10:30–11:30 Uhr, Konferenzraum Institut für Medizinische Biometrie und Statistik, Stefan-Meier-Str. 26, 1. OG

Vorherige Anmeldung per E-Mail (sec@imbi.uni-freiburg.de) ist erwünscht._____________

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann (im M.Sc. wie im M.Ed.).

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe, einem Oberseminar, Projektseminar …) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im M.Ed. und im Modul „Mathematik“ des M.Sc. gibt es eine mündliche Abschlussprüfung über den Stoff des Lesekurses, im Vertiefungsmodul des M.Sc. eine mündliche Abschlussprüfung über sämtliche Teile des Moduls. Ein Lesekurs zur Vorbereitung auf die Master-Arbeit kann im M.Sc. auch im Wahlmodul angerechnet werden (ohne Prüfung, nur Studieneistung).________________________________________________________________________________________________

Inhalt:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology or mathematical physics or a mix thereof.

The precise topic will be chosen at the end of the preceeding semester. The program will be made available via our web site.

The level is aimed at our doctoral students. Master students are very welcome to participate as well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. A. Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17:00 Uhr im Hörsaal II in der Albertstr. 23 b statt.

Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Eckerstraße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/