8.14 Komplexe Mannigfaltigkeiten

Inhalt:
Die Vorlesung ist mit der Theorie komplexer Mannigfaltigkeiten befasst. Beispiele für solche geometrische Objekte sind Gebiete in ℂ oder 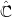(eindimensional) wie in der Funktionentheorie I behandelt bzw. auch Riemannsche Flächen oder Gebiete im ℂⁿ (n-dimensional) wie in der Funktionentheorie II vom WS 2010/11 betrachtet. Darüberhinaus gibt es eine unklassifizierbare Vielfalt komplexer Mannigfaltigkeiten. Die Vorlesung wird sich vor allem auf kompakte Mannigfaltigkeiten und die Konstruktion geometrischer Invarianten konzentrieren. Sie kann als Fortsetzung der Funktionentheorie II verstanden werden, jedoch wird der Besuch der Vorlesung Funktionentheorie II nicht vorausgesetzt.

Literatur:

1.)

Griffiths/Harris, Principles of Algebraic Geometry, Wiley, 1978

2.)

Huybrechts, Complex Geometry, Springer, 2005

3.)

Kaup/Kaup, Holomorphic Functions of Several Variables, de Gruyter, 1983