[next] [prev] [prev-tail] [tail] [up]

8.7 Numerik für Differentialgleichungen

Vorlesung:  

Numerik für Differentialgleichungen

  

Dozent:  

Prof. Dr. Gerhard Dziuk

  

Zeit/Ort:  

Di 11–13 Uhr, Weismann-Haus Albertstr. 21 a

  

Übungen:  

14-tgl. zweistündig

  

Tutorium:  

Dr. Philipp Reiter

  
 
_____________________________________________________________________

Inhalt:

Die meisten mathematischen Modelle für Probleme aus Mathematik und Naturwissenschaften bestehen aus Differentialgleichungen. Im einfachsten Fall handelt es sich um eine gewöhnliche Differentialgleichung (oder ein System gewöhnlicher Differentialgleichungen) der Form

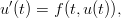
u′(t) = f (t,u(t)),
bei der alle Funktionen u = u(t) zu bestimmen sind, die diese Gleichung lösen. In den seltensten Fällen lassen sich Differentialgleichungen per Hand lösen. Meist verwendet man numerische Verfahren zur Lösung.

In dieser Vorlesung wird eine kurze Einführung in die Theorie und in die Standardmethoden zur analytischen Lösung von Differentialgleichungen gegeben. Darauf aufbauend werden numerische Verfahren zur Lösung gewöhnlicher Differentialgleichungen entwickelt, und es wird ihre Konsistenz, Stabilität und Konvergenz bewiesen.

Außerdem werden wir Differenzenverfahren für die einfachsten partiellen Differentialgleichungen (Wärmeleitungsgleichung, Wellengleichung, Poissongleichung) untersuchen.

Literatur:

  1. J. Stoer, R. Bulirsch: Numerische Mathematik I, II. Springer 2007, 2005.
  2. P. Deuflhard, A. Hohmann/F. Bornemann: Numerische Mathematik I, II. De Gruyter 2003, 2002.
_________________________________________

Typisches Semester:  

4. Semester

Studienschwerpunkt:  

BSc Mathematik, Lehramt, Diplom

Notwendige Vorkenntnisse:  

Grundvorlesungen in Linearer Algebra, Analysis und Numerik

Sprechstunde Dozent:  

Mi 14–15 Uhr, Hermann–Herder Str. 10, R 209

Sprechstunde Assistent:  

Mi 10–11 Uhr, Hermann–Herder Str. 10, R 208

 

[next] [prev] [prev-tail] [front] [up]