1.6 Algebraische Zahlentheorie

Inhalt:

Zahlentheorie beschäftigt sich mit den ganzen Zahlen und ihren Eigenschaften. Eine Kernfrage ist die Lösbarkeit von polynomialen Gleichungen in Z. Berühmt ist z.B. die Fermatsche Gleichung

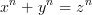
Hierbei ist es nützlich, auch Lösungen in Erweiterungen von Q zu betrachten. Im Fall der Fermatschen Gleichung sind die Einheitswurzeln (also ω mit ωⁿ = 1) wichtig. Ringe wie Z[ω] oder Z[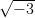] sind der Gegenstand der algebraischen Zahlentheorie.

In der Vorlesung werden diese Ringe eingeführt und ihre wichtigsten Eigenschaften bewiesen: Die Einheitengruppe ist endlich erzeugt, die Klassengruppe ist endlich. Danach wird es um die Überlagerungstheorie der Ganzheitsringe gehen. Wir werden immer wieder Hilfsmittel aus der Theorie der Ringe und Moduln benötigen. Diese wird daher ebenfalls entwickelt werden; ganze Ringerweiterungen, noethersche Ringe, Primideale, Lokalisierung, Bewertungen,…Dieser Stoff ist auch für die algebraische Geometrie wichtig.

Literatur:

1. P. Samuel, Théorie algébrique des nombres, Hermann, Paris 1967. (Gibt es auch auf Englisch.)
2. S. Lang, Algebraic Number Theory, 2. Aufl. Springer 1994.
3. J. Neukirch, Algebraische Zahlentheorie, Springer 1992.
4. J. Neukirch, Algebraic Number Theory, Springer 1999.