[next] [prev] [prev-tail] [tail] [up]

4.8 Geometrische Differentialgleichungen

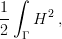
Seminar:

Geometrische Differentialgleichungen

  

Dozent:

Prof. Dr. Gerhard Dziuk

  

Zeit/Ort:

Mi 16-18 Uhr, SR 226, Hermann-Herder-Str. 10

  

Tutorium:

Paola Pozzi, PhD

  

Vorbesprechung:

Mi 13.2.2008, 13:15 Uhr, SR 226, Hermann-Herder-Str. 10
  

Teilnehmerliste:

Bei Frau Ruf, Raum 205, Hermann-Herder-Str.10

  

Web-Seite:

http://aam.mathematik.uni-freiburg.de/IAM/

  

Inhalt:

Geometrische Differentialgleichungen sind ein aktuelles Thema in theoretischer und angewandter Mathematik. Wir werden uns vor allem mit einem Problem vierter Ordnung befassen, das sowohl theoretisch als auch praktisch von Interesse ist. Die Biegeenergie einer Fläche oder Kurve Γ, Willmore-Funktional genannt, ist

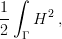
∫ 1- 2 2 Γ H ,
wobei H die mittlere Krümmung von Γ bezeichnet. Das Finden von stationären Lösungen ist ein klassisches Problem. Darüber hinaus ist der erst in den letzten Jahren analytisch untersuchte Willmore-Fluss von besonderem Interesse. Das ist die Methode des steilsten Abstiegs zum Willmore-Funktional. Schon bei Kurven und erst recht bei Flächen ist die Bewegung der elastischen Energie spannend und mathematisch äußerst interessant; auch ist dieser Fluss für zahlreiche Anwendungen (Physik, Biologie, Bildverarbeitung) von Interesse. Wir werden sowohl numerische als auch analytische Fragestellungen behandeln.

Literatur:

  1. T. J. Willmore, Riemannian Geometry, Oxford: Clarendon Press, 2002
  2. A. Dall’Acqua, K. Deckelnick, H. C. Grunau, Rotationally symmetric classical solutions to the Dirichlet problem for Willmore surfaces, Preprint Nr. 48/2007, Universität Magdeburg.
  3. G. Dziuk, Computational parametric Willmore Flow, Preprint Fakultät für Mathematik und Physik, Universität Freiburg, Nr. 07-13 (2007)

Typisches Semester:

ab 5. Semester

Studienschwerpunkt:

Angewandte Mathematik

Notwendige Vorkenntnisse:

Analysis III, Grundwissen über partielle Differentialgleichungen und Differentialgeometrie

Nützliche Vorkenntnisse:

Theorie und Numerik partieller Differentialgleichungen, Differentialgeometrie, Variationsrechnung

Sprechstunde Dozent:

Mi 11.30-12.30, Raum 209, Hermann- Herder Str. 10 und n.V.

Sprechstunde Assistentin:

Mo 14.15-15.15, Raum 223, Hermann-Herder Str. 10 und n.V.

[next] [prev] [prev-tail] [front] [up]