[next] [prev] [prev-tail] [tail] [up]

4.2 Wellengleichungen

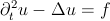
Seminar:

Wellengleichungen

  

Dozent:

Prof. Dr. Ernst Kuwert

  

Zeit/Ort:

Mi 14–16, SR 404, Eckerstr. 1

  

Tutorium:

Dr. Miles Simon

  

Vorbesprechung:

um 13:15 Uhr, SR 125, Eckerstr. 1

  

Teilnehmerliste:

Interessenten werden gebeten, sich in eine Liste einzutragen (Zi. 207, Eckerstr. 1, vormittags)

  

Web-Seite:

http://home.mathematik.uni-freiburg.de/analysis/

  

Inhalt:

Wellengleichungen beschreiben Ausbreitungs- und Schwingungsvorgänge in der Physik. Prototyp ist die klassische Wellengleichung

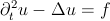
∂2tu - Δu = f
für eine Funktion u = u(x,t) auf ℝn × ℝ. Das zentrale Problem ist das Cauchyproblem, bei dem zu gegebenen Anfangsdaten u(⋅, 0) und ∂tu(⋅, 0) eine bzw. die Lösung gesucht wird. Wir beginnen mit den klassischen Lösungsansätzen mittels Darstellungsformeln und Fouriertransformation, sowie mit Energiemethoden. Ein Ziel ist die Existenz globaler Lösungen von nichtlinearen Wellengleichungen, also für alle Zeiten, mit kleinen Anfangsdaten. Hier spielt eine Sobolevungleichung von Klainerman eine Rolle. Ein weiteres mögliches Ziel sind Abschätzungen von Strichartz, die auch globale Lösungen für nichtlineare Wellengleichungen zu großen Anfangsdaten liefern.

Für seine Arbeiten, unter anderem auf diesem Gebiet, wurde Terence Tao 2006 eine Fields-Medaille verliehen.

Vorkenntnisse in Physik sind nicht erforderlich.

Typisches Semester:

ab 4. Semester

Studienschwerpunkt:

Analysis/Geometrie

Notwendige Vorkenntnisse:

Analysis III

Nützliche Vorkenntnisse:

Funktionalanalysis

Sprechstunde Dozent:

Mi 11:15–12:15 und n. V., R 208, Eckerstr. 1

Sprechstunde Assistent:

Mi 11:00–12:00, R 214, Eckerstr. 1

[next] [prev] [prev-tail] [front] [up]