Lehrveranstaltungen
1. Vorlesungen
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Analysis III |
| | |
Dozent: | Prof. Dr. Ernst Kuwert |
| | |
Zeit/Ort: | Mo, Mi 10–12, HS Rundbau, Albertstr. 21,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | N.N. |
| | |
| |
_______________________________________________________________
Inhalt:
Die Vorlesung gibt eine Einführung in die mehrdimensionale Maß- und Integrationstheorie
nach Lebesgue. Schwerpunkte sind allgemeine Maße und Integrale, Konvergenzsätze,
Integration im ℝn, Transformationssatz und Satz von Gauß, eventuell auch Integrale von
Differentialformen. Die Vorlesung ist für das weitere Studium in Analysis, Angewandter
Mathematik, Stochastik, Wahrscheinlichkeitstheorie und Geometrie relevant, auch in der
Physik.
Literatur:
-
1.)
- H. Amann, J. Escher: Analysis III (2. Auflage), Birkhäuser, 2008.
-
2.)
- J. Elstrodt: Maß- und Integrationstheorie (8. Auflage), Springer Spektrum, 2018.
-
3.)
- E. Kuwert: Vorlesungsskript Analysis III, verfügbar unter
http://home.mathematik.uni-freiburg.de/analysis/Analysis3WS1617/WS1617.pdf.
___
ECTS-Punkte: | 9 Punkte |
Notwendige Vorkenntnisse: | Analysis I und II, Lineare Algebra I und II |
Folgeveranstaltungen: | Funktionalanalysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Algebra und Zahlentheorie |
| | |
Dozent: | Prof. Dr. Stefan Kebekus |
| | |
Zeit/Ort: | Mo, Mi 8–10 Uhr, HS Weismann-Haus, Albertstr. 21a,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | Dr. Andreas Demleitner |
| | |
Web-Seite: | https://cplx.vm.uni-freiburg.de |
| | |
| |
_______________________________________________________________
Inhalt:
Diese Vorlesung setzt die Lineare Algebra fort. Behandelt werden Gruppen, Ringe, Körper sowie
Anwendungen in der Zahlentheorie und Geometrie. Höhepunkte der Vorlesung sind die
Klassifikation endlicher Körper, die Unmöglichkeit der Winkeldreiteilung mit Zirkel und Lineal,
die Nicht-Existenz von Lösungsformeln für allgemeine Gleichungen fünften Grades und das
quadratische Reziprozitätsgesetz.
Literatur:
-
1.)
- M. Artin: Algebra, Birkhäuser, 1998.
-
2.)
- S. Bosch: Algebra (9. Auflage), Springer Spektrum, 2020.
-
3.)
- S. Lang: Algebra (3. Auflage), Springer, 2002.
-
4.)
- W. Soergel: Vorlesungsskript Algebra und Zahlentheorie, verfügbar unter
http://home.mathematik.uni-freiburg.de/soergel/Skripten/XXAL.pdf.
___________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie II
Pflichtveranstaltung im 2-Hf-Bachelor |
Notwendige Vorkenntnisse: | Lineare Algebra I und II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Algebraische Gruppen sind Verallgemeinerungen der allgemeinen linearen Gruppen.
Aus der linearen Algebra über dem Körper der komplexen Zahlen und der Numerik
bekannte Tatsachen wie die Jordan-Zerlegung, die LU-Zerlegung oder die simultane
Trigonalisierbarkeit kommutierender Matrizen besitzen in diesem Kontext natürliche
Analoga. Die Theorie der algebraischen Gruppen, genauer der affinen algebraischen
Gruppen über einem algebraisch abgeschlossenen Körper, um die es hier gehen soll,
baut auf der kommutativen Algebra und der Theorie der affinen Varietäten und im
weiteren Verlauf auch der allgemeinen Varietäten auf, die in der Vorlesung auch in den
speziell benötigten Bereichen ausgebaut werden soll. Algebraische Gruppen spielen
eine zentrale Rolle in der Zahlentheorie, der Darstellungstheorie, der algebraischen
Geometrie, beim Studium endlicher Gruppen, und überhaupt in weiten Teilen der
Mathematik.
Literatur:
-
1.)
- A. Borel: Linear Algebraic Groups (Second Enlarged Edition), Springer, 1991.
-
2.)
- J.E. Humphreys: Linear Algebraic Groups, Springer, 1975.
-
3.)
- W. Soergel: Vorlesungsskript Affine algebraische Gruppen, verfügbar unter
http://home.mathematik.uni-freiburg.de/soergel/Skripten/XXAAG.pdf.
-
4.)
- T.A. Springer: Linear Algebraic Groups (Second Edition), Springer, 1998.
_______________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Kommutative Algebra und Einführung in die Algebraische
Geometrie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Die Vorlesung „Coxeter groups and Lie algebras“ ist eine gute
Ergänzung. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Coxeter groups and Lie algebras |
| | |
Dozent: | Dr. Johan Commelin |
| | |
Zeit/Ort: | Di, Do 14–16 Uhr, HS II, Albertstr. 23b,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | N.N. |
| | |
Web-Seite: | https://math.commelin.net/2020/coxeterlie/ |
| | |
| |
_______________________________________________________________
Content:
Coxeter groups and Lie algebras are central notions in so-called Lie theory. They appear
naturally in the study of representation theory of (certain) infinite groups, and have applications
in various other fields of mathematics such as differential geometry, algebraic geometry and
number theory.
In this course we will learn about the basic properties of Coxeter groups and reflection groups,
root systems, and Lie algebras. We will see how these concepts interact with each other, and
finally learn about the marvellous classification in terms of Dynkin diagrams: a certain type of
decorated graphs that naturally fall apart into four infinite lists and a handful of “exceptional”
examples.
Literature:
-
1.)
- N. Bourbaki: Éléments de Mathématique, Groupes et algèbres de Lie (Chapitres 4 à 6),
Springer, 2007.
-
2.)
- W. Soergel: Lecture notes Spiegelungsgruppen und Wurzelsysteme, available at
http://home.mathematik.uni-freiburg.de/soergel/Skripten/XXSPW.pdf.
__________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Lineare Algebra II, Algebra und Zahlentheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | This course will be taught in English.
Its content will have connections with the course on Lie groups
from last semester, but the overlap will be minimal. Lie groups
are not a prerequisite for this course. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die Differentialgeometrie beschreibt und untersucht die geometrischen Eigenschaften gekrümmter
Räume mit Methoden der Differentialrechnung. Daher findet die Differentialgeometrie
Anwendungen in anderen Bereichen der Mathematik und in der Physik, etwa in der
theoretischen Mechanik und der Relativitätstheorie.
In der Vorlesung werden zunächst die grundlegenden Begriffe und Methoden der
Differentialgeometrie eingeführt (wie differenzierbare Mannigfaltigkeiten, Vektorbündel und
Tensorfelder). Darauf aufbauend wird eine Einführung in die Riemannsche Geometrie gegeben,
die ein Teilgebiet der Differentialgeometrie ist. Hier werden insbesondere Geodätische und der
Riemannsche Krümmungstensor im Mittelpunkt stehen. Dort, wo es wenig Mehraufwand
bedeutet, werden auch die etwas allgemeineren Strukturen der semi-Riemannschen Geometrie
eingeführt, da diese zum Beispiel grundlegend für Anwendungen der Differentialgeometrie in der
Relativitätstheorie sind.
Literatur:
-
1.)
- M.P. do Carmo: Riemannian Geometry, Birkhäuser, 1992.
-
2.)
- J.M. Lee: Introduction to Smooth Manifolds (Second Edition), Springer, 2012.
-
3.)
- B. O’Neill: Semi-Riemannian Geometry with Applications to Relativity, Academic Press,
1983.
__________________________________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Analysis I und II, Lineare Algebra I und II sowie Analysis III
oder Elementare Differentialgeometrie |
Folgeveranstaltungen: | Differentialgeometrie II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Einführung in partielle Differentialgleichungen |
| | |
Dozent: | Prof. Dr. Guofang Wang |
| | |
Zeit/Ort: | Di, Do 12–14 Uhr, HS II, Albertstr. 23b,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | N.N. |
| | |
Web-Seite: | http://www.mathematik.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
Eine Vielzahl unterschiedlicher Probleme aus Naturwissenschaft und Geometrie führt auf
partielle Differentialgleichungen. Mithin kann keine Rede von einer allumfassenden Theorie
sein. Dennoch gibt es für lineare Gleichungen ein klares Bild, das sich an den drei
Prototypen orientiert: der Potentialgleichung -Δu = f, der Wärmeleitungsgleichung
∂tu - Δu = f und der Wellengleichung ∂t2u - Δu = f, die wir in der Vorlesung untersuchen
werden.
Literatur:
-
1.)
- E. Di Benedetto: Partial differential equations, Birkhäuser, 1995.
-
2.)
- L.C. Evans: Partial differential equations, Graduate Studies in Mathematics 19, AMS, 1998.
-
3.)
- Q. Han: A basic course in partial differential equations, Graduate Studies in Mathematics
120, AMS, 2011.
-
4.)
- F. John: Partial Differential Equations (Fourth Edition), Springer, 1982.
-
5.)
- J. Jost: Partielle Differentialgleichungen, Springer, 1998.
______________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine oder Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Analysis III |
Nützliche Vorkenntnisse: | Funktionalanalysis |
Folgeveranstaltungen: | Variationsrechnung |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Enge Verbindung zur Vorlesung „Einführung in Theorie und
Numerik partieller Differentialgleichungen“. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Einführung in Theorie und Numerik partieller
Differentialgleichungen |
| | |
Dozent: | Prof. Dr. Sören Bartels |
| | |
Zeit/Ort: | Mo, Mi 16–18 Uhr, HS II, Albertstr. 23b,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | N.N. |
| | |
| |
_______________________________________________________________
Inhalt:
Die Vorlesung beschäftigt sich mit der Analysis linearer partieller Differentialgleichungen sowie
der numerischen Approximation von deren Lösungen. Der Schwerpunkt liegt dabei auf der
Behandlung des Poisson-Problems, analytisch mit Hilbertraummethoden sowie numerisch mit
der Methode der Finiten Elemente. Diese Differentialgleichung beschreibt stationäre
Wärmeverteilungen und Diffusionsprozesse und ist wesentlicher Bestandteil vieler
mathematischer Beschreibungen realer Vorgänge. Die numerische Lösung basiert auf einer
Variationsformulierung und einer Zerlegung des physikalischen Gebiets in Dreiecke oder
Tetraeder. Damit wird ein kontinuierliches, unendlich-dimensionales Problem durch ein
endlich-dimensionales lineares Gleichungssystem approximiert, welches effizient am
Rechner gelöst werden kann. Die Exaktheit der Approximation in Abhängigkeit der
analytischen Eigenschaften der kontinuierlichen Lösung und die iterative Lösung des linearen
Gleichungssystems sind Schwerpunkte der Vorlesung. Im begleitenden Praktikum werden die
theoretischen Ergebnisse experimentell verifiziert.
Die Vorlesung ist so konzipiert, dass auch Lehramtsstudierende, die die Vorlesung
„Mehrfachintegrale“ oder die „Erweiterung der Analysis“ gehört haben, daran teilnehmen
können.
Literatur:
-
1.)
- S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.
-
2.)
- D. Braess: Finite Elemente (5. Auflage), Springer, 2013.
-
3.)
- M. Dobrowolski: Angewandte Funktionalanalysis (2. Auflage), Springer, 2010.
-
4.)
- L.C. Evans: Partial Differential Equations (Second Edition), AMS, 2010.
-
5.)
- B. Schweizer: Partielle Differentialgleichungen, Springer, 2013.
______________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Vorlesung Numerik |
Nützliche Vorkenntnisse: | Funktionalanalysis |
Folgeveranstaltungen: | Weiterführende Veranstaltungen zur Theorie und Numerik
partieller Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die Vorlesung Mathematische Statistik baut auf Grundkenntnissen aus der Vorlesung
Wahrscheinlichkeitstheorie auf. Das grundlegende Problem der Statistik ist, anhand einer
Stichprobe von Beobachtungen möglichst präzise Aussagen über den datengenerierenden Prozess
bzw. die den Daten zugrundeliegenden Verteilungen zu machen. Hierzu werden in der Vorlesung
die wichtigsten Methoden aus der statistischen Entscheidungstheorie wie Test-und
Schätzverfahren eingeführt.
Stichworte hierzu sind u.a. Bayes-Schätzer und -Tests, Neyman-Pearson-Testtheorie,
Maximum-Likelihood-Schätzer, UMVU-Schätzer, exponentielle Familien, lineare Modelle.
Weitere Themen sind Ordnungsprinzipien zur Reduktion der Komplexität der Modelle
(Suffizienz und Invarianz).
Statistische Methoden und Verfahren kommen nicht nur in den Naturwissenschaften und der
Medizin, sondern in nahezu allen Bereichen zum Einsatz, in denen Daten erhoben und analysiert
werden, so z.B. auch in den Wirtschaftswissenschaften (Ökonometrie) und Sozialwissenschaften
(dort vor allem in der Psychologie). Im Rahmen dieser Vorlesung wird der Schwerpunkt aber
weniger auf Anwendungen, sondern – wie der Name schon sagt – mehr auf der mathematisch
fundierten Begründung der Verfahren liegen.
Literatur:
-
1.)
- C. Czado, T. Schmidt: Mathematische Statistik, Springer, 2011.
-
2.)
- L. Rüschendorf: Mathematische Statistik, Springer Spektrum, 2014.
-
3.)
- M.J. Schervish: Theory of Statistics, Springer, 1995.
-
4.)
- H. Witting: Mathematische Statistik I, Teubner, 1985.
_________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Mathematische Logik
WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Zu Beginn der Vorlesung steht eine kurze Vorstellung der gängigsten Axiomensysteme der
Mathematik: das Zermelo-Fraenkel’sche System mit Auswahlaxiom (ZFC) und das
Axiomensystem von von Neumann, Bernays und Gödel (NBG). Die Axiome prägen unsere
Auffassung von den möglichen definierbaren oder vielleicht weniger konstruktiv gegebenen
mathematischen Objekten. Allerdings zeichnen sie kein vollständiges Bild eines einzigen
mathematischen Universums. Die Liste der herleitbaren mathematischen Aussagen ist
unvollständig: Für manche φ ist weder φ noch sein Negat aus ZFC beweisbar. Man sagt „φ ist
unabhängig von ZFC“.
Die bekannteste von ZFC unabhängige Aussage ist die Kontinuumshypothese, die sagt, dass es
genau ℵ1 reelle Zahlen gibt.
Die Vorlesung führt in die Technik der Unabhängigkeitsbeweise ein. Nach ersten einfachen
Forcings zur Kardinalzahlexponentiation werden wir ZF-Modelle ohne Auswahlaxiom und
iterierte Forcings (z.B. zum Nachweis der relativen Konsistenz von Martins Axiom)
kennenlernen. Es gibt ein Skript aus früheren Jahren.
Literatur:
-
1.)
- H.-D. Ebbinghaus: Einführung in die Mengenlehre (4. Auflage), Springer Spektrum, 2003.
-
2.)
- P. Eklof, A. Mekler: Almost Free Modules (Revised Edition), North-Holland, 2002.
-
3.)
- L. Halbeisen: Combinatorial Set Theory. With a Gentle Introduction to Forcing, Springer,
2012.
-
4.)
- T. Jech: Set Theory (The Third Millenium Edition, revised and expanded), Springer, 2003.
-
5.)
- K. Kunen: Set Theory. An Introduction to Independence Proofs, North Holland, 1980, elektronisch
verfügbar unter
https://pdfs.semanticscholar.org/8929/ab7afdb220d582e9880b098c23082da8bc0c.pdf.
-
6.)
- K. Kunen: Set Theory, College Publications, 2011.
-
7.)
- S. Shelah: Proper and Improper Forcing (Second Edition), Springer, 1997.
_______________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Grundvorlesungen |
Nützliche Vorkenntnisse: | Mathematische Logik |
Folgeveranstaltungen: | Seminar |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Nichtlineare Funktionalanalysis |
| | |
Dozent: | Prof. Dr. Michael Růžička |
| | |
Zeit/Ort: | Di, Do 10–12 Uhr, HS II, Albertstr. 23b,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | M.Sc. Alex Kaltenbach |
| | |
Web-Seite: | http://www.mathematik.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
Die Veranstaltung setzt die Vorlesung Funktionalanalysis fort. Die dort untersuchten linearen
Probleme sind oft nur Näherungen, wenn auch oft recht gute, der wahren nichtlinearen Probleme.
Diese Vorlesung beschäftigt sich mit Fragestellungen der nichtlinearen Funktionalanalysis,
d.h. der Untersuchung nichtlinearer Abbildungen zwischen unendlich-dimensionalen
Banachräumen. In der Vorlesung werden Fixpunktsätze, die Integration und Differentation in
Banachräumen, die Theorie monotoner Operatoren und der Abbildungsgrad behandelt. Dabei
wird besonders auf die Wechselwirkungen zwischen abtrakter Theorie und konkreten
Fragestellungen eingegangen.
Literatur:
-
1.)
- E. Zeidler: Nonlinear Functional Analysis and its Applications (Bände I-III), Springer,
1985–1990.
-
2.)
- M. Růžička: Nichtlineare Funktionalanalysis, Springer, 2004.
_________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik oder Reine Mathematik;
Kategorie III |
Notwendige Vorkenntnisse: | Funktionalanalysis |
Nützliche Vorkenntnisse: | Partielle Differentialgleichungen |
Folgeveranstaltungen: | Seminar zur Nichtlinearen Funktionalanalysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Stochastic Machine Learning |
| | |
Dozent: | Prof. Dr. Thorsten Schmidt |
| | |
Zeit/Ort: | Mo, Do 10–12 Uhr, SR 226, Hermann-Herder-Str. 10,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | M.Sc. Lars Niemann |
| | |
Web-Seite: | http://www.stochastik.uni-freiburg.de/schmidt |
| | |
| |
_______________________________________________________________
Content:
Machine Learning is one of the key technology in the recent developments in artificial
intelligence. In this lecture we will look at the most recent developments and concentrate on a
probabilistic perspective.
In particular we will study the reservoir computing paradigm, stochastic aspects of learning
like GANs, new discretizations schemes of stochastic differential equations and many
more.
A particular focus in the second half of the lecture will be on applications in Finance, like deep
pricing, deep calibration and deep hedging.
Literature will be announced in the lecture.____________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Stochastik (Teile 1 und 2) |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Die Vorlesung wird wahlweise auf deutsch oder englisch
gehalten werden. |
| |

WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die Vorlesung ist die erste Veranstaltung im Studiengang M.Sc. Mathematik, Studienschwerpunkt
Wahrscheinlichkeitstheorie, Finanzmathematik und Statistik, insbesondere in der Profillinie
Finanzmathematik. Sie schließt direkt an die Vorlesung „Wahrscheinlichkeitstheorie“ aus dem
WS 2019/20 an.
Ein stochastischer Prozess (Xt)t≥0 ist eine Familie von Zufallsvariablen. Einfache Beispielesind
Irrfahrten, Markov-Ketten, die Brown’sche Bewegung oder davon abgeleitete Prozesse. Vor allem
in der Modellierung von finanzmathematischen oder naturwissenschaftlichen Fragestellungen
spielt die Brown’sche Bewegung eine große Rolle.
Wir werden uns zunächst mit der reichhaltigen Klasse von Martingalen beschäftigen und die
wichtigen Martingalkonvergenzssätze kennen lernen. Anschließend konstruieren wir die
Brown’sche Bewegung und studieren ihre Pfadeigenschaften. Infinitesimale Charakteristiken
eines Markov-Prozesses werden durch Generatoren beschrieben, was eine Verbindung
zur Theorie von partiellen Differentialgleichungen ermöglicht. Im Sommersemester
2021 wird diese Veranstaltung durch die Vorlesung „Stochastische Integration und
Finanzmathematik“ fortgeführt.
Literatur:
-
1.)
- O. Kallenberg: Foundations of Modern Probability (Second Edition), Springer, 2002.
-
2.)
- A. Klenke: Wahrscheinlichkeitstheorie (3. Auflage), Springer Spektrum, 2013.
-
3.)
- D. Williams: Probability with Martingales, Cambridge University Press, 1991, elektronisch
verfügbar unter http://static.stevereads.com/papers_to_read/probability_with_martingales_williams_.pdf.
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Folgeveranstaltungen: | Stochastische Integration und Finanzmathematik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | The analytic subgroup theorem |
| | |
Dozentin: | Prof. Dr. Annette Huber-Klawitter |
| | |
Zeit/Ort: | Di, Do 8–10 Uhr, HS II, Albertstr. 23b,
ggf. als Online-Kurs |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | N.N. |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/arithgeom |
| | |
| |
_______________________________________________________________
Content:
Transcendence theory as part of number theory has a long and distinguished tradition in
Freiburg, beginning with Lindemann’s proof of transcendence of π and continuing with
Schneider’s results on transcendence of values of log.
In this lecture we want to study the most general result available at present, the analytic
subgroup theorem of Wüstholz. It characterises subgroups of commutative algebraic groups
which contain points defined over Q. The above mentioned special cases are easy consequences.
Its strength is in not only determining when a number is transcendental, but also giving
information on the Q-linear relations between them.
While the formulation uses the language of algebraic geometry and complex Lie groups, the
actual arguments are about constructing holomorphic functions. We will take the time to develop
the necessary background as well.
Literature:
-
1.)
- A. Baker, G. Wüstholz: Logarithmic forms and Diophantine geometry (New Mathematical
Monographs 9), Cambridge University Press, 2007.
-
2.)
- G. Wüstholz: Algebraische Punkte auf analytischen Untergruppen algebraischer Gruppen,
Ann. of Math. (2) 129 (1989), no. 3, 501–517.
____________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Funktionentheorie |
Nützliche Vorkenntnisse: | Grundkenntnisse in algebraischer Geometrie oder
Differentialgeometrie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Die Veranstaltung wird vermutlich auf Englisch stattfinden. |
| |

WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Das Problem der Axiomatisierung der Wahrscheinlichkeitstheorie wurde 1933 von
Kolmogorov gelöst: Eine Wahrscheinlichkeit ist ein Maß auf der Menge aller möglichen
Versuchsausgänge eines zufälligen Experiments. Von diesem Ausgangspunkt entwickelt sich die
gesamte moderne Wahrscheinlichkeitstheorie mit zahlreichen Bezügen zu aktuellen
Anwendungen.
Die Vorlesung ist eine systematische Einführung dieses Gebietes auf maßtheoretischer
Grundlage und beinhaltet unter anderem den zentralen Grenzwertsatz in der Version
von Lindeberg-Feller, bedingte Erwartungen und reguläre Versionen, Martingale und
Martingalkonvergenzsätze, das starke Gesetz der großen Zahlen und den Ergodensatz sowie die
Brownsche Bewegung.
Literatur wird in der Vorlesung bekanntgegeben werden.___________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie II |
Notwendige Vorkenntnisse: | Analysis III und Stochastik |
Folgeveranstaltungen: | Stochastische Prozesse (voraussichtl. im WS 2021/22);
Mathematische Statistik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Numerical Optimization |
| | |
Dozent: | Prof. Dr. Moritz Diehl |
| | |
Zeit/Ort: | Online-Kurs in Englisch |
| | |
Übungen: | Fr 14–16 Uhr, HS II, Albertstr. 23b, ggf. online |
| | |
Web-Seite: | https://www.syscop.de/teaching/ |
| | |
| |
_______________________________________________________________
Content:
The aim of the course is to give an introduction into numerical methods for the solution of
optimization problems in science and engineering. The focus is on continuous nonlinear
optimization in finite dimensions, covering both convex and nonconvex problems. The
course is accompanied by intensive computer exercises and divided into four major
parts:
-
1.
- Fundamental Concepts of Optimization : Definitions, Types, Convexity, Duality
-
2.
- Unconstrained Optimization and Newton Type Algorithms : Stability of Solutions,
Gradient and Conjugate Gradient, Exact Newton, QuasiNewton, BFGS and Limited
Memory BFGS, and GaussNewton, Line Search and Trust Region Methods,
Algorithmic Differentiation
-
3.
- Equality Constrained Optimization Algorithms : Newton Lagrange and Generalized
Gauss–Newton, Range and Null Space Methods, QuasiNewton and Adjoint Based
Inexact Newton Methods
-
4.
- Inequality Constrained Optimization Algorithms : KarushKuhnTucker Conditions,
Linear and Quadratic Programming, Active Set Methods, Interior Point Methods,
Sequential Quadratic and Convex Programming, Quadratic and Nonlinear
Parametric Optimization
Please read up on the website of the department and/or HISinOne for further information.
The lecture is accompanied by intensive weekly computer exercises based on MATLAB
(6 ECTS) and an optional project (3 ECTS). The project consists in the formulation and
implementation of a self-chosen optimization problem or numerical solution method, resulting in
documented computer code, a project report, and a public presentation.
Literature:
-
1.)
- A. Beck: Introduction to Nonlinear Optimization, MOS-SIAM, 2014.
-
2.)
- S. Boyd,
L. Vandenberghe: Convex Optimization, Cambridge University Press, 2004, elektronisch
verfügbar unter https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf.
-
3.)
- M. Diehl: Vorlesungsskript Numerical Optimization, verfügbar unter
https://www.syscop.de/files/2015ws/numopt/numopt_0.pdf.
-
4.)
- J. Nocedal, S.J. Wright: Numerical Optimization (Second Edition), Springer, 2006.
_______
ECTS-Punkte: | nur Vorlesung & Übungen: 6 Punkte; mit Projekt: 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Analysis I und II, Lineare Algebra I und II |
Nützliche Vorkenntnisse: | Einführung in die Numerik, Gewöhnliche
Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Diese Veranstaltung findet als Online-Kurs in englischer
Sprache statt. |
| |
Abteilung für
Quantitative Finanzmarktforschung
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Futures and Options |
| | |
Dozentin: | Prof. Dr. Eva Lütkebohmert-Holtz |
| | |
Zeit/Ort: | Mo 14–16 Uhr, Raum tba, ggf. als Online-Kurs |
| | |
Übungen: | Di 16–18 Uhr, Raum tba, ggf. online |
| | |
Tutorium: | Dr. Jonathan Ansari |
| | |
Web-Seite: | http://www.finance.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Content:
This course covers an introduction to financial markets and products. Besides futures and
standard put and call options of European and American type we also discuss interest-rate
sensitive instruments such as swaps.
For the valuation of financial derivatives we first introduce financial models in discrete time as
the Cox-Ross-Rubinstein model and explain basic principles of risk-neutral valuation. Finally, we
will discuss the famous Black–Scholes model which represents a continuous time model for
option pricing.
The course, which is taught in English, is offered for the first year in the Finance profile of the
M.Sc. Economics program as well as for students of M.Sc. and B.Sc. Mathematics and
M.Sc. Volkswirtschaftslehre.
For students who are currently in the B.Sc. Mathematics program, but plan to continue with the
special profile Finanzmathematik within the M.Sc. Mathematics, it is recommended to credit
this course for the latter profile and not for B.Sc. Mathematics.
Literature:
-
1.)
- D.M. Chance, R. Brooks: An Introduction to Derivatives and Risk Management, (10th
edition), Cengage, 2016.
-
2.)
- J.C. Hull: Options, Futures, and other Derivatives (10th edition), Pearson, 2018.
-
3.)
- S.E. Shreve: Stochastic Calculus for Finance I: The Binomial Asset Pricing Model, Springer,
2004.
-
4.)
- R.A. Strong: Derivatives. An Introduction, (Second edition), South-Western, 2004.
____________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III
Kann für die Spezialisierung Finanzmathematik
im Master-Studiengang auch als wirtschaftswissenschaftliches
Spezialisierungsmodul zählen. |
Nützliche Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Bitte registrieren Sie Sich vor Semesterbeginn für diesen Kurs
über das Belegverfahren von HISinOne! |
| |

WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Content:
Geometric data arise naturally in many scientific fields such as computational anatomy, brain
connectivity, molecular biology, meteorology, oceanology, online navigation, social networks, and
finance.
Moreover, in everyday-life applications, depth-enhanced image data is produced by time-of-flight
sensors in cars, game consoles, and recently also cell phone cameras. Analyzing such geometric
data is a major challenge, as the configuration spaces of e.g. curves, surfaces, diffeomorphisms,
graphs, etc. are infinite-dimensional nonlinear manifolds or more general stratified
spaces.
This course develops theoretical foundations for geometric data science, which are rooted in
infinite-dimensional Riemannian geometry and combine methods of machine learning, statistics,
and stochastics._________________________________________________________________________________________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Reine oder Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Differentialgeometrie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Die Vorlesung kann wahlweise auch auf Deutsch gehalten
werden. |
| |
2. Berufsorientierte Veranstaltungen
Mathematisches Institut
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Veranstaltung: | Lernen durch Lehren |
| | |
Dozent: | Alle Dozentinnen und Dozenten von Vorlesungen |
| | |
Zeit/Ort: | Termin und Ort der Einführungsveranstaltung werden
kurzfristig im Vorlesungsverzeichnis in HISinOne bekannt
gegeben |
| | |
| |
_______________________________________________________________
Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu
Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem
Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor
mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um
eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige
oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an
die Vorlesung).
Leistungsnachweis:
- Teilnahme an dem Einführungsworkshop. Voraussichtlich etwa zwei halbe Tage; einen
ungefähr in der ersten Vorlesungswoche und einen nach etwa vier Wochen. Näheres
wird rechtzeitig bekanntgegeben.
- Regelmäßige Teilnahme an der Tutorenbesprechung.
- Zwei gegenseitige Tutoratsbesuche
mit einem (oder mehreren) anderen Modulteilnehmer, welcher nach Möglichkeit die
gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten,
und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der
Einführungsveranstaltung).
Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert
werden und wird jeweils mit 3 ECTS-Punkten im Wahlbereich (im 2-Hf-Bachelor:
„Optionsbereich“) angerechnet. Im 2-Hf-Bachelor ist es bei Wahl der Lehramtsoption eine über
die 180 geforderter ECTS-Punkte hinausgehende Zusatzleistung. Es handelt sich um eine
Studienleistung, d.h. das Modul wird nicht benotet._________________________________________________
Abteilung für
Didaktik der Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Medieneinsatz im Mathematikunterricht |
| | |
Dozent: | Jürgen Kury |
| | |
Zeit/Ort: | Mo 15–18 Uhr, SR 127, Ernst-Zermelo-Str. 1,
ggf. als Online-Kurs |
| | |
Voranmeldung: | Interessierte Studierende melden ihren Teilnahmewunsch an diesem
Fachdidaktikseminar bitte per E-Mail an
|
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/didaktik/ |
| | |
| |
_______________________________________________________________
Inhalt:
Der Einsatz von Unterrichtsmedien im Mathematikunterricht gewinnt sowohl auf der Ebene der
Unterrichtsplanung wie auch der der Unterrichtsrealisierung an Bedeutung. Vor dem Hintergrund
konstruktivistischer Lerntheorien zeigt sich, dass der reflektierte Einsatz unter anderem von
Computerprogrammen die mathematische Begriffsbildung nachhaltig unterstützen kann. So
erlaubt beispielsweise das Experimentieren mit Computerprogrammen mathematische
Strukturen zu entdecken, ohne dass dies von einzelnen Routineoperationen (wie z. B.
Termumformung) überdeckt würde. Es ergeben sich daraus tiefgreifende Konsequenzen für den
Mathematikunterricht. Von daher setzt sich dieses Seminar zum Ziel, den Studierenden die
notwendigen Entscheidungs- und Handlungskompetenzen zu vermitteln, um zukünftige
Mathematiklehrer auf ihre berufliche Tätigkeit vorzubereiten. Ausgehend von ersten
Überlegungen zur Unterrichtsplanung werden anschließend Computer und Tablets hinsichtlich
ihres jeweiligen didaktischen Potentials untersucht und während eines Unterrichtsbesuchs mit
Lernenden erprobt.
Die dabei exemplarisch vorgestellten Systeme sind:
- dynamische Geometrie Software: Geogebra
- Tabellenkalkulation: Excel
- Apps für Smartphones und Tablets
Die Studierenden sollen Unterrichtssequenzen ausarbeiten, die dann mit Schülern erprobt und
reflektiert werden (soweit dies möglich sein wird).____________________________________________________
ECTS-Punkte: | 4 Punkte |
Verwendbarkeit: | Modul Fachdidaktische Entwicklung im M.Ed.;
Fachdidaktik-Seminar im Lehramt nach GymPO |
Nützliche Vorkenntnisse: | Grundvorlesungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |


WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Modul: | Fachdidaktische Forschung
Teil 1: Fachdidaktische Entwicklungsforschung zu ausgewählten
Schwerpunkten
Teil 2: Methoden mathematikdidaktischer Forschung
Teil 3: Begleitseminar zur Masterarbeit |
| | |
Dozenten: | Professorinnen und Professoren der PH Freiburg
Modulverantwortung: Prof. Dr. Timo Leuders |
| | |
Zeit/Ort: | Teil 1: Mo 14–16 Uhr, PH Freiburg, Räume des IMBF,
ggf. als Online-Kurs
Teil 2: Mo 10:00–13:00 Uhr im letzten Semesterdrittel,
PH Freiburg, Räume des IMBF
ggf. als Online-Kurs,
Teil 3: Termine nach individueller Vereinbarung |
| | |
Voranmeldung: | Studierende der Universität Freiburg, die an dieser Veranstaltung
teilnehmen möchten, melden Ihren Teilnahmewunsch bitte bis zum
31.07.2020 per Mail an didaktik@math.uni-freiburg.de |
| | |
Web-Seite: | https://www.ph-freiburg.de/fr/mathe/institut-personen/institut-person-tleuders.html |
| | |
| |
_______________________________________________________________
Studierende im M.Ed.-Studiengang Mathematik, die eine Masterarbeit in Fachdidaktik der
Mathematik schreiben möchten, müssen das dreiteilige Modul Fachdidaktische Forschung
absolvieren (beginnend mit Teil 1). Die Teilnahme ist durch die Betreuungskapazitäten begrenzt
und daher auch für die Studierenden, die eine fachdidaktische Arbeit schreiben möchten,
reserviert. Falls es mehr Interessenten als freie Plätze gibt, werden Sie frühzeitig über das weitere
Vorgehen informiert.
Inhalt:
Diese drei zusammengehörigen Veranstaltungen bereiten auf das Anfertigen einer empirischen
Masterarbeit in der Mathematikdidaktik vor. Das Angebot wird von allen Professorinnen und
Professoren mit mathematikdidaktischen Forschungsprojekten der Sekundarstufe 1 und 2
gemeinsam konzipiert und von einem dieser Forschenden durchgeführt. Im Anschluss besteht das
Angebot, bei einer dieser Personen eine fachdidaktische Masterarbeit anzufertigen – meist
eingebunden in größere laufende Forschungsprojekte.
In der ersten Veranstaltung findet eine Einführung in Strategien empirischer fachdidaktischer
Forschung statt (Forschungsfragen, Forschungsstände, Forschungsdesigns). Studierende vertiefen
ihre Fähigkeiten der wissenschaftlichen Recherche und der Bewertung fachdidaktischer
Forschung.
In der zweiten Veranstaltung (im letzten Semesterdrittel) werden die Studierenden durch
konkrete Arbeit mit bestehenden Daten (Interviews, Schülerprodukte, Experimentaldaten) in
zentrale qualitative und quantitative Forschungsmethoden eingeführt.
Die Haupziele des Moduls sind:
- Fähigkeit zur Rezeption mathematikdidaktischer Forschung zur Klärung
praxisrelevanter Fragen,
- Planung einer empirischen mathematikdidaktischen Masterarbeit.
Es wird abgehalten werden als Mischung aus Seminar, Erarbeitung von Forschungsthemen in
Gruppenarbeit sowie aktivem Arbeiten mit Forschungsdaten. Literatur wird abhängig von den
angebotenen Forschungsthemen innerhalb der jeweiligen Veranstaltungen angegeben
werden.
Die Teile können (in der richtigen Reihenfolge) auch in verschiedenen Semestern besucht werden,
zum Beispiel Teil 1 im zweiten Mastersemester und Teil 2 in der Kompaktphase des dritten
Mastersemesters nach dem Praxissemester.
_____________________________________________
ECTS-Punkte: | (für alle Teile des Moduls zusammen) 4 Punkte |
Verwendbarkeit: | Modul Fachdidaktische Forschung im M.Ed. |
Notwendige Vorkenntnisse: | Einführungsvorlesung in die Fachdidaktik der Mathematik |
Nützliche Vorkenntnisse: | Grundvorlesungen in Analysis und linearer Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Prakt. Übung zu: | Numerik (1. Teil der zweisemestrigen Veranstaltung) |
| | |
Dozent: | Prof. Dr. Patrick Dondl |
| | |
Zeit/Ort: | CIP-Pool 201, Hermann-Herder-Str. 10,
2-std. (14-täglich) n.V., ggf. als Online-Kurs |
| | |
Tutorium: | N.N. |
| | |
| |
_______________________________________________________________
Inhalt:
In der praktischen Übung zur Numerik-Vorlesung sollen die in der Vorlesung entwickelten und
analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird mit Hilfe der
kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme
geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.
Literatur:
-
1.)
- S. Bartels: Numerik 3x9, Springer, 2016.
___________________________________________________________________
ECTS-Punkte: | (für Teil 1 und 2 zusammen) 3 Punkte |
Notwendige Vorkenntnisse: | Vorlesung Numerik (parallel) |
Nützliche Vorkenntnisse: | Einführung in die Programmierung für Studierende der
Naturwissenschaften |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Prakt. Übung zu: | Stochastik |
| | |
Dozent: | Dr. Ernst August v. Hammerstein |
| | |
Zeit/Ort: | Online-Kurs, eventuell Do 10–12 Uhr als Livestream
bzw. Videokonferenz |
| | |
Tutorium: | Dr. Ernst August v. Hammerstein |
| | |
Anmeldung: | Bitte belegen Sie die Praktische Übung frühzeitig in HISinOne, da-
mit Sie per Mail über den genauen Ablauf und organisatorische
Details informiert werden können! |
| | |
Web-Seite: | https://www.stochastik.uni-freiburg.de/lehre/ws-2020-2021/prakueb-stochastik-ws-2020-2021 |
| | |
| |
_______________________________________________________________
Inhalt:
Die praktische Übung richtet sich an Hörerinnen und Hörer der Vorlesung Stochastik. Es
werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der
Vorlesung vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird
das frei verfügbare Open-Source-Statistikprogramm R verwendet werden. Nach einer
Einführung in R werden u.a. Verfahren der deskriptiven Statistik und graphischen
Auswertung von Daten betrachtet, die numerische Erzeugung von Zufallszahlen erläutert
sowie parametrische und nichtparametrische Tests und lineare Regressionsverfahren
diskutiert. Vorkenntnisse in R und/oder Programmierkenntnisse werden dabei nicht
vorausgesetzt.
Die praktische Übung ist für Studierende im (1-Hauptfach) B.Sc. Mathematik obligatorisch.
Studierende des 2-Hauptfächer-Bachelors mit Lehramtsoption können selbstverständlich
ebenfalls teilnehmen und die praktische Übung als Teil des Wahlpflichtmoduls Mathematik im
Rahmen ihres Studiengangs verbuchen. Im Studiengang Master of Education kann die
Veranstaltung als Mathematische Ergänzung belegt werden.
Für das Nacharbeiten der Lektionen und zur Lösung der darin enthaltenen Übungen sollten
alle Teilnehmenden die dazu benötigte Software (R und RStudio) auf ihren eigenen
Rechnern installieren. Genauere Anleitungen hierzu sowie Links zum Download der
kostenlosen Programme werden frühzeitig auf der o.g. Webseite bekannt gegeben
werden.
Zu den einzelnen Lektionen der praktischen Übung wird ein ausführliches Skriptum bereitgestellt
werden. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern
möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher
zu R empfohlen werden.______________________________________________________________________________________
ECTS-Punkte: | 3 Punkte |
Verwendbarkeit: | Pflichtveranstaltung im B.Sc. Mathematik
2-Hf-Bachelor mit Lehramtsoption: Möglicher Teil des
Wahlpflichtmoduls Mathematik
M.Ed.: Möglich als Mathematische Ergänzung (sofern nicht
schon im 2-Hf-Bachelor-Studiengang belegt) |
Notwendige Vorkenntnisse: | Analysis I und II, Lineare Algebra I und II, Stochastik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Prakt. Übung zu: | Einführung in Theorie und Numerik partieller
Differentialgleichungen |
| | |
Dozent: | Prof. Dr. Sören Bartels |
| | |
Zeit/Ort: | CIP-Pool Raum 201, Hermann-Herder-Str. 10, 2-std. n.
V.,
ggf. als Online-Kurs |
| | |
Tutorium: | N.N. |
| | |
| |
_______________________________________________________________
Inhalt:
In der praktischen Übung zur Vorlesung sollen die in der Vorlesung entwickelten und analysierten
Algorithmen praktisch umgesetzt und getestet werden. Dies wird mit Hilfe der kommerziellen
Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen.
Elementare Programmierkenntnisse werden vorausgesetzt.
Literatur:
-
1.)
- S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.
_______
ECTS-Punkte: | 3 Punkte |
Verwendbarkeit: | Wahlmodul im B.Sc. und M.Sc. Mathematik
Mathematische Ergänzung im M.Ed. |
Notwendige Vorkenntnisse: | Vorlesung „Einführung in Theorie und Numerik partieller
Differentialgleichungen“ (parallel) |
Nützliche Vorkenntnisse: | Praktische Übung zu Numerik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
3. Seminare
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Proseminar: | Erzeugende Funktionen |
| | |
Dozent: | Prof. Dr. Stefan Kebekus |
| | |
Zeit/Ort: | Di 10–12 Uhr, SR 226, Hermann-Herder-Str. 10,
ggf. als Online-Seminar |
| | |
Tutorium: | Dr. Andreas Demleitner |
| | |
Vorbesprechung: | Montag, 27.07.2020, um 10:00 Uhr im virtuellen
BBB-Sprechstundenraum vKebekus
Passwort vKebekus20208 |
| | |
Web-Seite: | https://cplx.vm.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
Wie viele Möglichkeiten gibt es, aus 2 und 5-Cent-Stücken einen vorgegebenen Betrag zu
kombinieren? Wie findet man eine explizite Formel für die n-te Fibonacci-Zahl? Wie viele
zusammenhängende markierte Graphen gibt es zu fester Knotenzahl?
Diese und viele andere Fragen verbindet, dass man sie mit Hilfe erzeugender Funktionen
„lösen“ kann: Wir wollen im Seminar den Ansatz verfolgen, die auftretenden Folgen als
Koeffizienten einer Potenzreihe zu interpretieren und die so entstehenden Funktionen
untersuchen.
Der größte Teil des Seminars orientiert sich entlang des Buches von Herbert Wilf.
Literatur:
-
1.)
- H. Wilf: Generatingfunctionology, online verfügbar unter
https://www.math.upenn.edu/~wilf/gfology2.pdf.
-
2.)
- J. Wolfart: Einführung in die Zahlentheorie und Algebra (2. Auflage), Springer Vieweg, 2011.
Notwendige Vorkenntnisse: | Grundvorlesungen Lineare Algebra und Analysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Proseminar: | Der Volterra-Operator |
| | |
Dozentin: | Dr. Susanne Knies |
| | |
Zeit/Ort: | Mi 12–14 Uhr, SR 404, Ernst-Zermelo-Str. 1,
ggf. als Online-Seminar |
| | |
Tutorium: | M.Sc. Luca Courte |
| | |
Voranmeldung: | Teilnahmewunsch bitte per Mail an
mitteilen, bitte mit Angabe zu Studiengang (B.Sc. oder
2-Hf-Bachelor) und Fachsemester. |
| | |
Vorbesprechung: | voraussichtlich: 29.07.20, 10 Uhr, Raum wird den
Interessentinnen und Interessenten per Mail bekannt
gegeben |
| | |
Web-Seite: | http://www.mathematik.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
Durch den Volterra-Operator
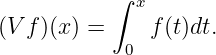 wird
eine lineare Abbildung definiert. Für diesen Operator ist es bereits mit einfachen Mitteln
möglich, eine Theorie im unendlichdimensionalen Banachraum C([0,a]) aufzubauen.
wird
eine lineare Abbildung definiert. Für diesen Operator ist es bereits mit einfachen Mitteln
möglich, eine Theorie im unendlichdimensionalen Banachraum C([0,a]) aufzubauen.
Literatur:
-
1.)
- J.H. Shapiro: Volterra Adventures, Student Mathematical Library 85, AMS, 2018.
_____________
Notwendige Vorkenntnisse: | Analysis I und II, Lineare Algebra I und II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Proseminar: | Das BUCH der Beweise |
| | |
Dozent: | Dr. Ernst August v. Hammerstein |
| | |
Zeit/Ort: | Do 14–16 Uhr, SR 404, Ernst-Zermelo-Str. 1,
ggf. als Online-Seminar |
| | |
Tutorium: | Dr. Ernst August v. Hammerstein |
| | |
Voranmeldung: | Interessenten melden bitte ihren Teilnahmewunsch bis spätestens
zum 28.07.2020 per Mail an
|
| | |
Vorbesprechung: | Mittwoch, 29.07.2020, um 14:00 Uhr per Videokonferenz im
virtuellen BigBlueButton-Sprechstundenraum vHammerstein |
| | |
Web-Seite: | http://www.stochastik.uni-freiburg.de/lehre/ws-2020-2021/proseminar-buchbeweise-ws-2020-2021 |
| | |
| |
_______________________________________________________________
Inhalt:
Dem großen ungarischen Mathematiker Paul Erdős zufolge sollte jeder Mathematiker an das
BUCH glauben, in dem Gott die perfekten Beweise für mathematische Sätze aufbewahren würde.
In ihrer Annäherung an das BUCH haben Aigner und Ziegler eine große Anzahl von Sätzen
zusammengetragen, deren elegante, raffinierte und überraschende Beweise (nach Meinung der
Autoren) wahren BUCH-Beweisen schon recht nahe kommen dürften. Die dort vorgestellten
Resultate sind weitgehend unabhängig voneinander und vielfältig über verschiedene Gebiete der
Mathematik verteilt, von Zahlentheorie, Geometrie, Analysis und Kombinatorik hin zur
Graphentheorie.
In den Proseminarvorträgen soll jeweils eines dieser Resultate, basierend auf dem zugehörigen
Kapitel des Buches, genauer vorgestellt und erläutert werden. Dabei können (in gewissen
Grenzen) Interessen und Themenwünsche der Teilnehmenden berücksichtigt werden. Alle ins
Auge gefassen Themen sind im Wesentlichen mit den üblicherweise im Grundstudium
Mathematik erworbenen Kenntnissen zugänglich, an manchen Stellen ist aber auch ein wenig
Fachwissen aus weiterführenden Vorlesungen sicher hilfreich.
Literatur:
-
1.)
- M. Aigner, G.M. Ziegler: Das BUCH der Beweise (4. Auflage), Springer, 2015.
Als elektronischer Volltext (innerhalb des Uni-Netzes!) verfügbar unter
http://www.redi-bw.de/start/unifr/EBooks-springer/10.1007/978-3-662-44457-3
_
Notwendige Vorkenntnisse: | Lineare Algebra I und II, Analysis I und II |
Nützliche Vorkenntnisse: | Je nach Vortragsthema u.U. etwas Stochastik oder Algebra
und Zahlentheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Diese Proseminar ist insbesondere auch für Studierende des
2-Hf-Bachelor-Studienganges geeignet. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Proseminar: | Geometrie von Kurven |
| | |
Dozent: | Prof. Dr. Ernst Kuwert |
| | |
Zeit/Ort: | Di 14–16 Uhr, SR 404, Ernst-Zermelo-Str. 1,
ggf. als Online-Seminar |
| | |
Tutorium: | N.N. |
| | |
Voranmeldung: | Teilnahmewunsch bitte bis zum 16.07.2020 per E-Mail an
ernst.kuwert@math.uni-freiburg.de |
| | |
Vorbesprechung: | Montag, 20.07.2020, 14:00 Uhr im SR 404,
Ernst-Zermelo-Str. 1 |
| | |
| |
_______________________________________________________________
Inhalt:
Es sollen Kurven in der Ebene und im Raum untersucht werden. Die lokale Geometrie einer
Kurve wird durch ihre Krümmung beschrieben. Globale Größen sind zum Beispiel die Länge, der
eingeschlossene Flächeninhalt oder die Windungszahl. Mit den Methoden aus Analysis und
Lineare Algebra I,II lassen sich eine Reihe schöner Aussagen zum Wechselspiel zwischen lokaler
und globaler Geometrie beweisen.
Das Proseminar wendet sich an Studierende mit Interesse an Analysis oder Geometrie. Weitere
Literatur wird ggf. bei der Vorbesprechung genannt.
Literatur:
-
1.)
- C. Bär: Elementare Differentialgeometrie (2. Auflage), de Gruyter 2010, 26–91.
-
2.)
- E. Kuwert: Vorlesungsskript Elementare Differentialgeometrie, verfügbar unter
http://home.mathematik.uni-freiburg.de/analysis/ElDiffGeo18/skript.pdf, 3–33.
__
Notwendige Vorkenntnisse: | Analysis und Lineare Algebra I,II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Kristallographische Gruppen |
| | |
Dozentin: | Prof. Dr. Katrin Wendland |
| | |
Zeit/Ort: | Blockseminar 17.–19. Februar 2021, ggf. als
Online-Seminar |
| | |
Tutorium: | Dr. Severin Barmeier |
| | |
Voranmeldung: | Bei Interesse bitte Voranmeldung bis 23.07.2020 per E-Mail an
unter Angabe von Studiengang, Verwendungswunsch und Vorkennt-
nissen |
| | |
Vorbesprechung: | Donnerstag, 30.07.2020, 12 Uhr im
virtuellen BBB-Seminarraum Anderssen (Zugangsdaten folgen
nach Voranmeldung) |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/mathphys/lehre/WiSe20/KristallographischeGruppen.html |
| | |
| |
_______________________________________________________________
Inhalt:
Das Seminar stellt ein Angebot an M.Ed.-Studierende im Praxissemester für das Modul
„Mathematische Ergänzung“ dar, es können aber auch Proseminar-Vorträge und vereinzelte
Vorträge Richtung Algebra oder Topologie für das Bachelor-Seminar im B.Sc. vergeben
werden.
Kristallographische Gruppen sind unendliche Gruppen, die die Symmetrien von Kristallen (also
von Atomen, Ionen oder Molekülen, die in einer Kristallstruktur angeordnet sind) beschreiben.
Schon Ende des 19. Jahrhunderts wurde gezeigt, dass es (im 3-dimensionalen Raum) genau 230
verschiedene Arten dieser Gruppen gibt, und die Zuordnung der Symmetriegruppe wird
standardmäßig, neben z.B. der chemischen Zusammensetzung, als Grundeigenschaft auf dem
Datenblatt eines Kristalls aufgeführt.
Dass es nur endlich viele kristallographische Gruppen gibt, lässt sich schon mit linearer Algebra
beweisen, sogar in beliebiger Dimension! In höheren Dimensionen spricht man deswegen auch
von Raumgruppen. In Dimension 2 werden diese wiederum auch Wandmustergruppen
(engl. wallpaper groups) genannt; hier gibt es genau 17 dieser Gruppen, die eben die möglichen
Symmetrien von Tapetenmustern beschreiben, z.B.

Neben Anwendungen in der Kristallographie oder beim Erstellen von Tapetenmustern gibt es
aber auch sehr schöne Verbindungen zu anderen Bereichen der Mathematik, wie Topologie,
Differentialgeometrie, Darstellungstheorie von endlichen Gruppen bis hin zur algebraischen
Zahlentheorie.
In diesem Seminar werden wir uns dem Thema der kristallographischen Gruppen widmen, die
Hauptresultate über die Endlichkeit der kristallographischen Gruppen zeigen und zugleich einige
dieser Querverbindungen aufgreifen.
Literatur:
-
1.)
- L.S. Charlap: Bieberbach groups and flat manifolds, Springer, 1986, Kap. I.
-
2.)
- D.L. Johnson: Symmetries, Springer, 2001, Kap. 1–8.
-
3.)
- A. Szczepański: Geometry of crystallographic groups, World Scientific, 2012, Kap. 1–3.
_______
Verwendbarkeit: | Proseminar
(im B.Sc. Mathematik oder 2-Hf-Bachelor-Studiengang) oder
Seminar im M.Ed. bzw. B.Sc. (auch Bachelor-Seminar) |
Notwendige Vorkenntnisse: | Grundvorlesungen für Proseminarvorträge, Algebra oder
Topologie für Seminarvorträge |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Bitte melden Sie Ihr Interesse an dem Seminar mit
Studiengang, Verwendungswunsch (Seminar, Proseminar,
Bachelor-Seminar) und Vorkenntnissen wie oben angegeben
an; eine Teilnehmerliste wird nicht vorab ausliegen. Vorträge
dürfen auf Deutsch oder auf Englisch gehalten werden. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Wir wollen uns in diesem Seminar grob der historischen Entwicklung folgend mit der
Invariantentheorie beschäftigen.
Die klassische Invariantentheorie des 19. Jahrhunderts behandelt die Wirkung einer Gruppe
G auf dem Polynomring k[x1,…,xn] über einem Körper k. Typische Fragestellungen
beschäftigen sich mit den invarianten Polynomen. Diese bilden den Invariantenring
k[x1,…,xn]G – eine k-Unteralgebra von k[x
1,…,xn] – und man kann beispielsweise versuchen,
Erzeuger dieser k-Algebra zu finden, sowie Relationen zwischen diesen Erzeugern. Diese
sogenannten Fundamentalen Probleme lassen sich beispielsweise für abelsche Gruppen,
endliche Untergruppen von SL2(ℂ), oder klassische Lie-Gruppen wie SLn(ℂ), On(ℂ)
lösen.
Die moderne Sichtweise der geometrischen Invariantentheorie wiederum interpretiert die
Elemente des Invariantenrings als Funktionen auf einer Quotientenvarietät und untersucht
wechselseitig Geometrie und Algebra.
Darüberhinaus haben seit Ende des 20. Jahrhunderts algorithmische Methoden große Bedeutung
erlangt. Diese bauen unter anderem auf der Theorie der Gröbnerbasen auf, welche es
beispielsweise erlauben, die Frage nach der Zugehörigkeit eines Polynoms zu einem Ideal oder der
Dimension einer Varietät eindeutig zu beantworten. Somit können sie geometrisch als – unter
gewissen Gesichtspunkten – ideale Gleichungen für algebraische Varietäten angesehen
werden.
Literatur:
-
1.)
- D. Cox, J. Little, D. O’Shea: Ideals, varieties, and algorithms, Springer, 2015.
-
2.)
- H. Kraft: Geometrische Methoden in der Invariantentheorie, Springer Vieweg, 1984.
-
3.)
- M.D. Neusel: Invariant theory, AMS, 2007.
-
4.)
- B. Sturmfels: Algorithms in invariant theory (Second Edition), Springer, 2008.
_________________
Notwendige Vorkenntnisse: | Vorlesung Kommutative Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Flächen |
| | |
Dozent: | Prof. Dr. Guofang Wang |
| | |
Zeit/Ort: | Mi 16–18 Uhr, SR 404, Ernst-Zermelo-Str. 1,
ggf. als Online-Seminar |
| | |
Tutorium: | N.N. |
| | |
Voranmeldung: | Vornmeldung per Mail an Guofang.Wang@math.uni-freiburg.de |
| | |
Vorbesprechung: | Montag, 27.07.2020, 14:00–15:00 Uhr im virtuellen
BBB-Sprechstundenraum vWang |
| | |
Web-Seite: | http://www.mathematik.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
Wir untersuchen in diesem Seminar sowohl Minimalflächen als auch Flächen mit konstanter
mittlerer Krümmung.
Minimalflächen sind Flächen im Raum mit „minimalem“ Flächeninhalt und lassen sich mit Hilfe
holomorpher Funktionen beschreiben. Sie treten u.a. bei der Untersuchung von Seifenhäuten
und der Konstruktion stabiler Objekte (z.B. in der Architektur) in Erscheinung. Bei der
Untersuchung von Minimalflächen kommen elegante Methoden aus verschiedenen
mathematischen Gebieten wie der Funktionentheorie, der Variationsrechnung, der
Differentialgeometrie und der partiellen Differentialgleichungen zur Anwendung. Wir
untersuchen auch Flächen mit konstanter mittlerer Krümmung als Verallgemeinerung der
Minimalflächen.
Das Seminar eignet sich sowohl für Studierende im B.Sc. und M.Sc. Mathematik als auch für
Lehramtsstudierende.
Literatur:
-
1.)
- T.H Colding, W.P. Minicozzi II: Minimal Surfaces, Graduate Studies in Mathematics 121,
AMS, 2011.
-
2.)
- J.-H. Eschenburg, J. Jost: Differentialgeometrie und Minimalflächen (3. Auflage), Springer,
2014.
-
3.)
- E. Kuwert: Vorlesungsskript Einführung in die Theorie der Minimalflächen, verfügbar unter
http://home.mathematik.uni-freiburg.de/analysis/lehre/skripten/MinimalflaechenSS98/minimalfl_240815.pdf.
-
4.)
- W.H. Meeks III, J. Pérez: A survey on classical minimal surface theory, verfügbar unter
https://www.ugr.es/~jperez/papers/monograph-book2.pdf.
-
5.)
- R. Osserman: A survey of minimal surfaces, Dover, 2002.
_____________________________________________
Notwendige Vorkenntnisse: | Analysis III oder Mehrfachintegrale und Funktionentheorie |
Nützliche Vorkenntnisse: | Partielle Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Mathematische Logik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Ramsey-Theorie |
| | |
Dozentin: | Prof. Dr. Heike Mildenberger |
| | |
Zeit/Ort: | Di 16–18 Uhr, SR 404, Ernst-Zermelo-Str. 1,
ggf. als Online-Seminar |
| | |
Tutorium: | N.N. |
| | |
Voranmeldung: | Bitte schicken Sie vor dem 20.07.2020 eine E-Mail an
um Ihren Teilnahmewunsch abzugeben und die Kontaktdaten zu
erfahren. |
| | |
Vorbesprechung: | Montag, 20.07.2020, um 15 Uhr im virtuellen
BBB-Sprechstundenraum vMildenberger |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/mildenberger/veranstaltungen/ws20/ramseytheorie.html |
| | |
| |
_______________________________________________________________
Inhalt:
Die Lehre und die Forschung über Färbungen großer Grundräume mit wenigen Farben und
Finden recht großer homogener Teilräume heißt Ramsey-Theorie nach Frank Plumpton Ramsey
(1903–1930). In diesem Seminar studieren wir Färbungen von Bäumen.
Im Forcing von Modellen für echte Abschwächungen des Auswahlaxioms spielen
Baumfärbungseigenschaften eine Rolle für die Existenz von Filtern symmetrischer Untergruppen.
Ein berühmter Satz über homogene Niveaumengen auf Produkten von Bäumen ist der
Satz von Halpern und Läuchli von 1966, zu dem erst Anfang der 2000er Jahre ein
„metamathematikfreier“ Beweis gefunden wurde. Dieser Satz ist ein wesentlicher Baustein im
Satz von Halpern und Lévy, dass das Primidealtheorem nicht das Auswahlaxiom impliziert. Im
Seminar sollen die trickreichen, aber recht elementaren kombinatorischen Schlüsse in Todorcevics
Beweis des Halpern-Läuchli-Satzes studiert werden. Zu diesem Thema können Abschlussarbeiten
vergeben werden.
Literatur:
-
1.)
- N. Dobrinen, D. Hathaway: The Halpern-Läuchli theorem at a measurable cardinal,
J. Symb. Log. 82 (2017), 1560–1575.
-
2.)
- P. Erdős, A. Hajnal, A. Máté, R. Rado: Combinatorial Set Theory: Partition Relations for
Cardinals, North-Holland, 1984.
-
3.)
- J.D. Halpern, H. Läuchli: A partition theorem, Trans. Amer. Math. Soc. 124 (1966),
360–367.
-
4.)
- S. Todorcevic: Introduction to Ramsey Spaces, Princeton University Press, 2010.
_______________
Nützliche Vorkenntnisse: | Grundvorlesungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Numerische Mathematik |
| | |
Dozent: | Prof. Dr. Sören Bartels |
| | |
Zeit/Ort: | Mo 14–16 Uhr, SR 226, Hermann-Herder-Str. 10,
ggf. als Online-Seminar |
| | |
Tutorium: | M.Sc. Jakob Keck, M.Sc. Philipp Tscherner |
| | |
Voranmeldung: | Voranmeldung per E-Mail an Frau Tress
elvira.tress@mathematik.uni-freiburg.de |
| | |
Vorbesprechung: | Mittwoch, 22.07.2020, 13:15 Uhr, per Videokonferenz |
| | |
| |
_______________________________________________________________
Inhalt:
Im Seminar sollen weiterführende Fragestellungen der numerischen Mathematik diskutiert
werden. Dazu gehören die Themen:
- Stabilität der Gauß-Elimination [5]
- Konvergenz des QR-Verfahrens für Eigenwertberechnungen [6, 4]
- Varianten des Simplex-Verfahrens [1, 3]
- Entwicklung hochdimensionaler Quadraturformeln [5]
- Optimalitätsbedingungen für konvexe Optimierungsprobleme [3]
- Mehrdimensionale Interpolation [1]
- Approximation mit Bernstein-Polynomen [7]
- Relaxationsverfahren zur Lösung linearer Gleichungssysteme [6]
- Vorkonditioniertes CG-Verfahren [1]
- Methode von Hyman zur Eigenwertberechnung [6]
- GMRES-Verfahren als Erweiterung des CG-Verfahrens [6]
- Quasi-Newton-Verfahren [2]
Die Themen sind voneinander unabhängig. Bei Anmeldung zum Seminar können zwei
Wunschthemen angegeben werden, darüberhinaus erfolgt die Vergabe zufällig.
Literatur:
-
1.)
- S. Bartels: Numerik 3x9, Springer, 2016.
-
2.)
- C. Geiger, C. Kanzow: Numerische Verfahren zur Lösung unrestringierter
Optimierungsaufgaben, Springer, 1999.
-
3.)
- C. Geiger, C. Kanzow: Theorie und Numerik restringierter Optimierungsaufgaben, Springer,
2002.
-
4.)
- H. Harbrecht: Vorlesungsskript Numerische Mathematik, Universität Basel, 2013.
-
5.)
- N.J. Higham: Accuracy and stability of numerical algorithms (Second Edition), SIAM, 2002.
-
6.)
- R. Plato: Numerische Mathematik kompakt (4. Auflage), Springer Vieweg, 2010.
-
7.)
- A. Salgado, S. Wise: Vorlesungsskript Graduate Numerical Analysis, Universität Knoxville,
2020, verfügbar unter http://www.math.utk.edu/~swise/NABook/book.pdf.
_____________
Notwendige Vorkenntnisse: | Vorlesung Numerik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Stochastische Modelle der Epidemiologie |
| | |
Dozent: | Prof. Dr. Peter Pfaffelhuber |
| | |
Zeit/Ort: | Fr 10–12 Uhr, SR 404, Ernst-Zermelo-Str. 1,
ggf. als Online-Seminar |
| | |
Tutorium: | M.Sc. Timo Enger |
| | |
Voranmeldung: | Interessenten melden bitte ihren Teilnahmewunsch per Mail an
unter Nennung von Name, Vorname, Immatrikulationsnummer,
Studiengang und Studiensemester (in diesem Studiengang) bis
spätestens 24.07.2020. |
| | |
Vorbesprechung: | Do, 30.07.2020, 11:00 Uhr, Ort wird noch bekanntgegeben |
| | |
Web-Seite: | http://www.stochastik.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
In den letzten Monaten hört man immer wieder von mathematischen Modellen der
Epidemiologie. Wir werden in diesem Seminar auf Grundlage eines Sammelbandes von Tom
Britton und Etienne Pardoux (Stochastic Epidemic Models with Inference, Springer, 2019) und
aktuellen Veröffentlichungen auf diese Modelle eingehen.___________________________________________
Notwendige Vorkenntnisse: | Stochastische Prozesse |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Institut für
Medizinische Biometrie und
Statistik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Medical Data Science |
| | |
Dozent: | Prof. Dr. Harald Binder |
| | |
Zeit/Ort: | Mi 10–11:30 Uhr, HS Medizinische Biometrie und Statistik,
Stefan-Meier-Str. 26, ggf. als Online-Seminar |
| | |
Voranmeldung: | Rechtzeitig vor der Vorbesprechung per E-Mail an
sec@imbi.uni-freiburg.de |
| | |
Vorbesprechung: | Mittwoch, 22.07.2020, 11:30–12:30 Uhr, online
(Zugangsdaten bei Anmeldung) |
| | |
Web-Seite: | http://portal.uni-freiburg.de/imbi/lehre/WS/Hauptseminar |
| | |
| |
_______________________________________________________________
Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft
ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder
allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data
Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als
Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt
werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue
thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein
oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik
dienen.
Hinweise auf einführende Literatur werden in der Vorbesprechung gegeben.___________________
Notwendige Vorkenntnisse: | Gute Kenntnisse in Wahrscheinlichkeitstheorie und
Mathematischer Statistik |
Folgeveranstaltungen: | Das Seminar kann als Vorbereitung für eine Masterarbeit
dienen. |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
|
| |
Abteilung für
Quantitative Finanzmarktforschung
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Quantitative Finance |
| | |
Dozenten: | Prof. Dr. Eva Lütkebohmert-Holtz und Dr. Mirko
Schäfer |
| | |
Zeit/Ort: | tba, ggf. als Online-Seminar |
| | |
Tutorium: | N.N. |
| | |
Anmeldung: | Registration details will be announced soon on our website (see
below) |
| | |
Web-Seite: | http://www.finance.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Content:
After successful completion of the course, the student is able to
- describe scenarios for climate change and for the transformation to a low-carbon
economy,
- discuss current global trends for the investment in low-carbon energy systems,
- relate climate risks and policy risks to systemic risk in financial systems,
- communicate key points from current reports and scientific articles covering the global
energy transition, climate risks, and their relation to the financial system.
Topics of the seminar include:
- Scenarios for climate change and for the transition to a low-carbon economy
- The role of climate change and the energy transition for financial stability
- The interplay between policy, investment dynamics, and technological development
- Classification of sustainable investments and assessment of climate-related risks
- The impact of the energy transition on capital markets
- The fossil fuel divestment movement
Literature:
-
1.)
- A call for action – Climate change as a source of financial risk, Network for Greening the
Financial System (NGFS), 2019.
-
2.)
- Annual Review 2018–2019, Carbon Tracker, 2019.
-
3.)
- World Energy Investment 2020, International Energy Agency (IEA), 2020.
-
4.)
- E. Camiglio et al.: Climate change challenges for central banks and financial regulators,
Nature Climate Change 8 (2018), 462–468.
Further literature will be announced in the seminar.
________________________________________
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | The seminar will be held in English. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Viele Fragestellungen aus Naturwissenschaft und Technik führen auf zeitabhängige, nichtlineare
partielle Differentialgleichungen. Am Beispiel der nichtlinearen Wärmeleitungsgleichung und der
Navier-Stokes Gleichung erarbeiten wir uns Methoden, um diese lösen zu können. Die
behandelten Themen eignen sich als Grundlage für Bachelor- und Masterarbeiten.__________
Notwendige Vorkenntnisse: | Einführung in Theorie und Numerik Partieller
Differentialgleichungen, Funktionalanlysis |
Nützliche Vorkenntnisse: | Bochner-Räume, partielle Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Nichtlineare Elastizitätstheorie |
| | |
Dozent: | Prof. Dr. Patrick Dondl |
| | |
Zeit/Ort: | Mo 12–14 Uhr, HS II, Albertstr. 23b,
ggf. als Online-Seminar |
| | |
Tutorium: | M.Sc. Luca Courte und M.Sc. Coffi Hounkpe |
| | |
Voranmeldung: | Interessenten melden bitte ihren Teilnahmewunsch per E-Mail an
patrick.dondl@mathematik.uni-freiburg.de unter Angabe von
Studiengang, Verwendungswunsch und Vorkenntnissen. |
| | |
Vorbesprechung: | Montag, 05.10.2020, 14:00 Uhr im virtuellen
BBB-Sprechstundenraum vDondl |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agdo/lehre/ws20/elast/ |
| | |
| |
_______________________________________________________________
Inhalt:
In diesem Seminar beschäftigen wir uns mit Aspekten der nichtlinearen Elastizitätstheorie,
welche eine wichtige Basis zur Modellierungen von Festkörpern darstellt. Das mathematische
Fundament zur Behandlung der Elastizitätstheorie wurde von John Ball in seinem seminalen
Artikel von 1977 gelegt [1]. Wir werden die mathematischen Schwierigkeiten, die die Behandlung
dieser Probleme darstellt, im Seminar kennenlernen [3].
Des Weiteren werden wir auch angewandtere Aspekte betrachten, wie Dimensionsreduktion, das
Falten von Papier und der Mikrostruktur von Metallen. Dimensionsreduktion ist ein Prozess, bei
welchen man herausfinden möchte, wie das effektive Verhalten von z.B. dünnen Platten
beschrieben werden kann, wenn man diese als zwei-dimensionale Objekte modelliert [2, 4]. Die
Mikrostruktur, welche sich in bestimmten Metalllegierungen formt, kann ebenfalls über
nichtlineare Elastizitätstheorie beschrieben werden [5].
Das Seminar richtet sich insbesondere an Masterstudierende, bestimmte Vorträge eignen sich
allerdings auch als Themen für Bachelorarbeiten.
Literatur:
-
1.)
- J.M. Ball: Convexity conditions and existence theorems in nonlinear elasticity,
Arch. Rat. Mech. Anal. 63 (1977), 337–403.
-
2.)
- S. Conti, F. Maggi: Confining thin elastic sheets and folding paper,
Arch. Rat. Mech. Anal. 187 (2008), 1–48.
-
3.)
- B. Dacorogna: Direct Methods in the Calculus of Variations, Springer, 2008.
-
4.)
- G. Friesecke, R.D. James, S. Müller: A theorem on geometric rigidity and the derivation
of nonlinear plate theory from three-dimensional elasticity, Comm. Pur. Appl. Math. 55
(2002), 1461–1506.
-
5.)
- R.V. Kohn, S. Müller: Surface energy and microstructure in coherent phase transitions,
Comm. Pur. Appl. Math. 47 (1994), 405–435.
___________________________________________________________
Notwendige Vorkenntnisse: | Vorlesung Funktionalanalysis sowie eine Vorlesung zu PDE |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
4. Projektseminare, Lesekurse
und Kolloquien
Mathematisches Institut
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Lesekurs: | Wissenschaftliches Arbeiten |
| | |
Dozent: | Alle Professor/inn/en und Privatdozent/inn/en des
Mathematischen Instituts |
| | |
Zeit/Ort: | nach Vereinbarung |
| | |
| |
_______________________________________________________________
Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen
Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen
einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im
Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit
einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der
Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der
Lesekurs im Idealfall als Vorbereitung auf die Master-Arbeit dient (im M.Sc. wie im
M.Ed.).
Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen
(typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums,
eventuell Vorträge in einer Arbeitsgruppe, einem Oberseminar, Projektseminar …) werden zu
Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung
sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.
Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung
bestanden ist oder nicht. Im M.Ed. und im Modul „Mathematik“ des M.Sc. gibt es eine
mündliche Abschlussprüfung über den Stoff des Lesekurses, im Vertiefungsmodul des M.Sc. eine
mündliche Abschlussprüfung über sämtliche Teile des Moduls. Ein Lesekurs zur Vorbereitung auf
die Master-Arbeit kann im M.Sc. auch im Wahlmodul angerechnet werden (ohne Prüfung, nur
Studieneistung).
Im M.Sc.-Studiengang ist daran gedacht, dass Sie einen, maximal zwei Lesekurse absolvieren.
________________________________________________________________________________________
Verwendbarkeit: | M.Ed.: Modul Wissenschaftliches Arbeiten
M.Sc.: Vertiefungsmodul, Wahlmodul, Modul Mathematik |
Notwendige Vorkenntnisse: | hängen vom einzelnen Lesekurs ab |
| |
Abteilung für
Reine Mathematik
WS2020/21
 ______________________________________________________________________
______________________________________________________________________
Projektseminar: | Seminar des Graduiertenkollegs GK 1821 |
| | |
Dozent: | Die Dozentinnen und Dozenten des Graduiertenkollegs |
| | |
Zeit/Ort: | Mi 14–16 Uhr, SR 404, Ernst-Zermelo-Str. 1,
ggf. als Online-Seminar |
| | |
Web-Seite: | https://www.gk1821.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Content:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in
Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology
or mathematical physics or a mix thereof.
The precise topic will be chosen at the end of the preceeding semester. The program will be
made available via our web site.
The level is aimed at our doctoral students. Master students are very welcome to participate as
well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. Annette
Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________
ECTS-Punkte: | im M.Sc.-Studiengang 6 Punkte |
Notwendige Vorkenntnisse: | je nach Thema, meist algebraische Geometrie |
| |

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________


 ______________________________________________________________________
______________________________________________________________________
![]()
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
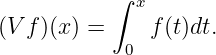

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________