Allgemeine Hinweise

das kommentierte Vorlesungsverzeichnis gibt über das Lehrangebot des Mathematischen Instituts im aktuellen Semester Auskunft. Welche Vorlesungen, Seminare und Übungen Sie belegen können und müssen, sowie Informationen zum Studienverlauf entnehmen Sie am besten den Informationsseiten zu den einzelnen Studiengängen, die Sie im Internet unter https://www.math.uni-freiburg.de/lehre/ finden. Bitte beachten Sie, dass die Anforderungen in den einzelnen Studiengängen unterschiedlich sein können, in Abhängigkeit von der jeweils gültigen Prüfungsordnung. Informationen zu Prüfungen und insbesondere zu ihrer Anmeldung finden Sie auf den Internetseiten des Prüfungsamts.

Hinweise für Studienanfänger

An unserem Institut können Sie Mathematik mit folgenden Zielen studieren:

• Mathematik-bezogene Ausbildung für Beschäftigungen in Wirtschaft, Industrie, Banken, Forschung …: Am besten beginnen Sie Ihr Studium mit dem Studiengang Bachelor of Science in Mathematik (im Folgenden auch kurz B.Sc. Mathematik). Nach einer Regelstudienzeit von sechs Semestern können Sie den Studiengang Master of Science in Mathematik (M.Sc. Mathematik) anschließen.
• Ausbildung zum Lehramt an Gymnasien: In diesem Fall beginnen Sie Ihr Studium mit dem Studiengang Polyvalenten Zwei-Hauptfächer-Bachelor (im Folgenden auch kurz 2-Hf-Bachelor), in dem Sie neben Mathematik ein zweites Fach studieren. In dem Studiengang wählen Sie die Lehramtsoption, indem Sie im Optionsbereich die vorgesehenen Module in Bildungswissenschaften und Fachdidaktik belegen. Nach einer Regelstudienzeit von sechs Semestern schließen Sie den Studiengang Master of Education (M.Ed.) an.
• Bei Interesse an einer bestimmten Fächerkombination können Sie den 2-Hf-Bachelor auch ohne Lehramtsoption studieren. Falls sich im Laufe des Studiums ein stärkeres Interesse an Mathematik und der Wunsch einer auf dem Mathematikstudium aufbauenden Beschäftigung ergibt, sollten Sie einen Wechsel in den B.Sc.-Studiengang in Betracht ziehen.

Allgemeine Hinweise zur Planung des Studiums

Spätestens ab Beginn des 3. Semesters sollten Sie die Beratungsangebote des Mathematischen Instituts in Anspruch nehmen (allgemeine Studienberatung des Studiengangkoordinators, Studienfachberatung der einzelnen Abteilungen, Mentorenprogramm, Beratung durch Dozentinnen und Dozenten). Im Rahmen des Mentorenprogramms der Fakultät wird Ihnen in der Regel am Ende Ihres 3. Semesters eine Dozentin oder ein Dozent als Mentor zugewiesen, die oder der Sie zu Beratungsgesprächen einladen wird. Die Teilnahme an diesem Programm wird nachdrücklich empfohlen.

Zur sinnvollen Planung Ihres Studiums beachten Sie bitte folgende allgemeine Hinweise:

• Mittlere oder höhere Vorlesungen: Inwieweit der Stoff mittlerer oder höherer Vorlesungen als Vorbereitung für Abschlussarbeiten und -prüfungen ausreicht oder ergänzt werden sollte, geht entweder aus den Kommentaren hervor oder muss rechtzeitig mit den Prüferinnen und Prüfern abgesprochen werden. Insbesondere gilt dies für die mündliche Prüfung im Vertiefungsmodul des M.Sc. Eine Liste der Arbeitsgebiete der Professorinnen, Professoren und Privatdozenten finden Sie auf den Seiten 10/11.
• Seminare: Die Teilnahme an Seminaren setzt in der Regel den vorherigen Besuch einer oder mehrerer weiterführender Vorlesungen voraus. Die Auswahl dieser Vorlesungen sollte rechtzeitig erfolgen. Eine Beratung durch Dozentinnen und Dozenten oder Studienberaterinnen und Studienberater der Mathematik erleichtert Ihnen die Auswahl.

Unabhängig hiervon sollten Sie folgende Planungsschritte beachten:

• B.Sc. Mathematik:
  Spätestens am Ende des ersten Studienjahrs: Wahl des Anwendungsfaches
  Ende des 3. Semesters: Planung des weiteren Studienverlaufs
  Beginn des 5. Semesters: Wahl geeigneter Veranstaltungen zur Vorbereitung der Bachelor-Arbeit
• 2-Hf-Bachelor:
  Für den Einstieg ins gymnasiale Lehramt ist die Belegung der Lehramtsoption im Wahlbereich erforderlich. Diese setzt sich aus einem Fachdidaktikmodul in jedem Fach und einem bildungswissenschaftlichen Modul zusammen.
  Das Fachdidaktik-Modul in Mathematik wird von der Abteilung Didaktik der Mathematik für das dritte Studienjahr angeboten (Sommer- und Wintersemester). Das bildungswissenschaftliche Modul besteht aus der Vorlesung „Einführung in die Bildungswissenschaften“ (Mo 14–16 Uhr im Wintersemester, ab erstem Semester möglich), und dem Orientierungspraktikum mit Vor- und Nachbereitung (zwischen Winter- und Sommersemester).
• Lehramts-Studiengang nach GymPO
  Nehmen Sie rechtzeitig Kontakt mit den Prüferinnen und Prüfern auf, um die Prüfungsgebiete im Staatsexamen abzusprechen. Durch die Wahl der Veranstaltung(en) im Modul „Mathematische Vertiefung“ können Sie die Auswahl für die Prüfungsgebiete erhöhen.
  Falls Sie die Wissenschaftliche Arbeit in Mathematik schreiben möchten, empfiehlt es sich, die Wahl der Veranstaltungen (weiterführende Vorlesung, Seminar) mit der Betreuerin/dem Betreuer der Arbeit abzusprechen.
  Bitte beachten Sie, dass einige Veranstaltungen im Zuge der Umstellung auf 2-Hf-Bachelor/M.Ed. nicht mehr angeboten werden und Sie ggf. stattdessen die vorgesehenen Ersatzveranstaltungen besuchen müssen.

Als Ersatz für eine Orientierungsprüfung müssen alle Studierenden in einem Bachelor-Studiengang im Fach Mathematik gewisse Studienleistungen bis zum Ende des dritten Fachsemesters absolviert haben.

Im B.Sc.-Studiengang Mathematik müssen die beiden Klausuren zu Analysis I und zu Lineare Algebra I bis zum Ende des dritten Fachsemesters bestanden sein.

Im 2-Hf-Bachelor-Studiengang muss im Fach Mathematik mindestens eine der beiden Klausuren zu Analysis I oder zu Lineare Algebra I bis zum Ende des dritten Fachsemesters bestanden sein. (Die jeweils andere Klausur muss auch bestanden werden, aber ohne Frist. Im zweiten Fach muss zudem die Orientierungsprüfung bestanden werden.)

An alle Studierenden

In fast allen Modulen besteht kein Zulassungszusammenhang zwischen Studien- und Prüfungsleistung. Dies bedeutet, dass Sie z. B. eine Prüfung zu einer weiterführenden Vorlesung anmelden und ablegen dürfen, bevor Sie die Studienleistung in den zugehörigen Übungen erbracht haben. Die Studienleistung muss dann allerdings nachgeholt werden; bis dahin ist das Modul nicht abgeschlossen und es werden keine ECTS-Punkte angerechnet.

Bitte beachten Sie:

• Es gibt Zulassungsbedingungen zu den mündlichen Prüfungen in Analysis und in Linearer Algebra in den Bachelor-Studiengängen.
• Es gibt Zulassungsbedingungen zu den Abschlussarbeiten.
• Studien- und Prüfungsleistungen in einem Modul müssen inhaltlich zusammengehören. Wenn Sie zu einer nicht regelmäßig angebotenen Vorlesung eine Prüfung absolvieren ohne die Studienleistung bestanden zu haben, haben Sie in naher Zukunft keine Möglichkeit mehr, die Studienleistung nachzuholen. In diesem Fall bleibt die bestandene Prüfung ohne Wert, da das Modul nicht abgeschlossen werden kann.
• Da die Übungen auch der Prüfungsvorbereitung dienen und Sie für eine Prüfung nur eine begrenzte Anzahl von Wiederholungsversuchen haben, raten wir dringend davon ab, eine Prüfung zu absolvieren, ohne die zugehörige Studienleistung erworben zu haben.

Weitere Informationen finden Sie auf den Webseiten des Prüfungsamts Mathematik
(https://www.math.uni-freiburg.de/lehre/pruefungsamt/index.html).

Aus der folgenden Tabelle geht hervor, in welchen Modulen aus welchen Studiengängen die im aktuellen Semester angebotenen Veranstaltungen verwendet werden können. Grundsätzlich dürfen in einem Master-Studiengang keine Veranstaltungen absolviert werden, die in dem zugrundeliegenden Bachelor-Studiengang bereits verwendet wurden. Bei Rückfragen wenden Sie sich bitte an die Studienberatung.

Bitte beachten Sie:

• Fortgeschrittene Veranstaltungen setzen Vorkenntnisse voraus. Es ist Ihrer Verantwortung überlassen einzuschätzen, ob Sie über ausreichende Vorkenntnisse verfügen oder bereit sind, fehlende Vorkenntnisse nachzuarbeiten. Es ist erlaubt, höhere, typischerweise für den M.Sc.-Studiengang angebotene Vorlesungen in anderen Studiengängen zu verwenden; aufgrund der geforderten Vorkenntnisse werden sie aber nur in Ausnahmefällen in Frage kommen. In der Tabelle ist zwischen „typisch“ (d. h. besonders geeignet und regelmäßig angeboten) und „möglich“ (setzt Vorkenntnisse voraus oder wird selten angeboten) unterschieden. Diese Trennung ist allerdings etwas künstlich und nicht klar definiert.
• Im B.Sc. Mathematik müssen über den Pflichtbereich hinaus mindestens vier 4-stündige Vorlesungen mit 2-stündigen Übungen (à 9-ECTS-Punkte) absolviert werden. Mindestens eine davon muss aus dem Bereich der Reinen Mathematik stammen. Welche Vorlesungen zur Reinen Mathematik zählen, finden Sie in den Kommentaren der einzelnen Vorlesungen in der Rubrik „Verwendbarkeit“ und in der Tabelle in der Spalte für das Modul „Reine Mathematik“ im M.Sc.-Studiengang.

  Einige Vorlesungen, typischerweise aus dem Bereich der Funktionalanalysis, zählen sowohl zur Reinen als auch zur Angewandten Mathematik.

• Im Groben ergibt sich die Verwendbarkeit von Vorlesungen aus der Einteilung in drei Kategorien:

  Veranstaltungen der Kategorie I – das sind im Wesentlichen die Pflichtveranstaltungen des B.Sc. – dürfen im M.Sc. nicht verwendet werden.

  Veranstaltungen der Kategorie II sind typische für den B.Sc. geeignete Wahlpflichtveranstaltungen. Sie dürfen im M.Sc. nur in den Modulen „Reine Mathematik“, „Angewandte Mathematik“ und im Wahlmodul verwendet werden, nicht aber im Modul „Mathematik“ und im Vertiefungsmodul. Die im M.Sc. geforderte Studienleistung beinhaltet bei Vorlesungen der Kategorie II auch die Klausur.

  In der Regel sind die Vorlesungen der Kategorie II auch die für das Modul „Mathematische Vertiefung“ im M.Ed. bzw. Lehramt nach GymPO und die für die Option individuelle Schwerpunktgestaltung im 2-Hf-Bachelor geeigneten Veranstaltungen.

  Veranstaltungen der Kategorie III sind für den M.Sc. geeignete Wahlpflichtveranstaltungen. Sie dürfen auch in den anderen Studiengängen verwendet werden.

● Pflicht oder typisch , etc. nur Teil des Moduls (MSc: nur nach Absprache) ◯ möglich (Vorkenntnisse beachten!) Zahl: ECTS-Punkte

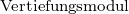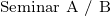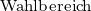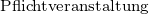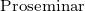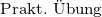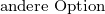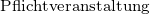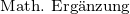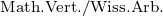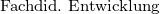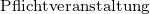Veranstaltung, \

B .  S c .

M .  S c .

2 - H f . - B .

M .  E d .

G y m P O  H f

Algebraische Gruppen

◯

●

●

➒

➈

◯

◯

Algebra und Zahlentheorie

●

●

➒

●

—

●

Analysis I

●

—

●

—

●

Analysis III

●

—

➒

●

●

Coxeter Groups and Lie Algebras

◯

●

●

➒

➈

◯

◯

Didaktik der Funktionen und der Analysis

—

—

●

(als Ersatz)

Didaktik der Stochastik und der Algebra

—

—

●

(als Ersatz)

Differentialgeometrie I

●

●

●

➒

➈

◯

◯

Einführung in die Fachdidaktik der Mathematik

—

—

●

—

(als Ersatz)

Einführung in partielle Differentialgleichungen

●

●

●

➒

➈

◯

◯

Einführung in Theorie und Numerik part. Differentialgl.

●

●

●

➒

➒

●

●

Erweiterung der Analysis

—

—

—

●

Fachdidaktikseminare

➃

—

—

●

●

Futures and Options

➏

➏

➅

◯

➅

Geometric Data Science

➅

➏

➅

◯

➅

Lineare Algebra I

●

—

●

—

●

Mathematische Statistik

◯

●

●

➒

➈

◯

◯

Mengenlehre – Unabhängigkeitsbeweise

●

●

●

➒

➒

●

●

Nichtlineare Funktionalanalysis

◯

●

●

●

➒

➈

◯

◯

Numerical Optimization (mit Projekt)

●

●

●

➒

➈

◯

◯

Numerical Optimization (ohne Projekt)

➏

➏

➅

◯

Numerik (zweisemestrig)

●

—

●

—

●

Praktische Übung zu „Einführung in Theorie und …“

➌

➌

◯

➂

◯

Praktische Übung zu „Numerik“ (zweisemestrig)

●

—

●

➌

●

Praktische Übung zu „Stochastik“

●

—

●

➌

●

Proseminare

●

—

●

—

●

Seminare

◯

●

➏

●

➏

◯

➏

●

◯

●

Stochastic Machine Learning

◯

●

●

➒

➈

◯

◯

Stochastik (zweisemestrig)

●

—

●

—

●

Stochastische Prozesse

◯

●

●

➒

➈

◯

◯

The analytic subgroup theorem

◯

●

●

➒

➈

◯

◯

Wahrscheinlichkeitstheorie

●

●

➒

➒

●

●

Wissenschaftliches Arbeiten

—

◯

➈

—

●

—