[next] [prev] [prev-tail] [tail] [up]

7.7 Einführung in die Theorie und Numerik partieller Differentialgleichungen

Vorlesung:  

Einführung in die Theorie und Numerik partieller Differentialgleichungen

  

Dozent:  

Prof. Dr. D. Kröner

  

Zeit/Ort:  

Mo, Mi, 12–14 Uhr, HS II, Albertstr. 23 b

  

Übungen:  

2-std. n. V.

  

Tutorium:  

J. Daube

  

Web-Seite:  

http://aam.mathematik.uni-freiburg.de/IAM/

  
 

Inhalt:
Partielle Differentialgleichungen sind Gleichungen, die einen Zusammenhang zwischen einer Funktion u, deren partiellen Ableitungen und weiteren gegebenen Funktionen beinhalten, z. B.

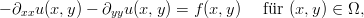
- ∂ u(x,y) - ∂ u(x,y) = f (x,y) fu¨r (x,y ) ∈ Ω, xx yy
wobei Ω eine Teilmenge des ℝ2 ist. Diese Differentialgleichung ist vom elliptischen Typ und steht im Mittelpunkt der Vorlesung. Das zu lösende Problem besteht nun darin, zu gegebenen Funktionen f : Ω → ℝ2 und g : ∂Ω → ℝ2 eine Funktion u : Ω → ℝ2 zu finden, welche die obige Differentialgleichung löst und die Randbedingung
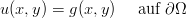
u(x,y) = g (x, y) auf ∂ Ω
erfüllt.
Partielle Differentialgleichungen treten oft als Modelle für physikalische Vorgänge auf. Das obige Beispiel beschreibt z. B. die Temperaturverteilung u in einem Raum Ω, wenn der Raum gemäß der Funktion f aufgeheizt wird und die Wände (∂Ω) des Raumes auf der Temperatur g gehalten werden.
Da sich eine explizite Lösung nur in Spezialfällen finden lässt, muss man sich zunächst auf die Untersuchung der Frage, ob es überhaupt Lösungen gibt und wenn ja, wie viele, beschränken. Der nächste Schritt, der den Schwerpunkt der Vorlesung bildet, ist die numerische Berechnung von Näherungslösungen mit Hilfe der Finite-Elemente-Methode. Neben der Darstellung des Verfahrens steht die Herleitung von Fehlerabschätzungen im Vordergrund. Parallel zu der Vorlesung werden eine Übung und ein Praktikum (siehe Kommentar zum Praktikum) angeboten.

Literatur:

1.)
D. Braess, Finite Elemente, Springer, Berlin (2007)
2.)
G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010)
______

Typisches Semester:  

5. Semester

ECTS-Punkte:  

9 Punkte

Master-Studiengang:  

geeignet für das Modul Angewandte Mathematik

Notwendige Vorkenntnisse:  

Analysis und Lineare Algebra

Sprechstunde Dozent:  

Di, 13–14 Uhr und n. V., Raum 215, Hermann-Herder-Str. 10

Sprechstunde Assistent:  

Do, 11–12 Uhr und n. V., Raum 212, Hermann-Herder-Str. 10
 

[next] [prev] [prev-tail] [front] [up]