[next] [prev] [prev-tail] [tail] [up]

7.5 Variationsrechnung

Vorlesung:  

Variationsrechnung

  

Dozent:  

Prof. Dr. Ernst Kuwert

  

Zeit/Ort:  

Mo, Mi, 14–16 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-std. n. V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/analysis

  
 

Inhalt:

Gegenstand der Vorlesung ist die mehrdimensionale Variationsrechnung. Wir betrachten auf Ω ⊂ ℝn Funktionale bzw. Variationsintegrale der Form

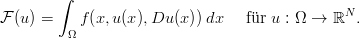
∫ F (u) = f(x,u (x ),Du (x))dx fur u : Ω → ℝN . Ω ¨
Beispiele sind Bogenlänge und Flächeninhalt, sowie Energien von Feldern in der Physik. Die zentrale Fragestellung ist die Existenz von Minimierern sowie deren Regularität. Da sich aus der Endlichkeit des Funktionals keine punktweise Kontrolle der Funktionen u ergibt, werden wir Räume von verallgemeinerten Funktionen, sogenannte Sobolevräume, einführen und in diesen das Existenzproblem lösen. Sofern die Zeit das erlaubt, wollen wir auch Verfahren zur Konstruktion nichtminimierender Lösungen vorstellen.

Literatur:

1.)
Struwe, Michael, Variational Methods. Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 4th edition. Springer-Verlag, Berlin, 2008.
___________

Typisches Semester:  

5. und 7.

ECTS-Punkte:  

9 Punkte

Master-Studiengang:  

geeignet für das Modul Reine Mathematik

Notwendige Vorkenntnisse:  

Analysis III

Sprechstunde Dozent:  

Mi, 11:15–12:15 Uhr und n. V., Raum 208, Eckerstr. 1

 

[next] [prev] [prev-tail] [front] [up]