1.8 Modelltheorie
Vorlesung: | Modelltheorie |
| | |
Dozent: | Martin Ziegler |
| | |
Zeit/Ort: | Mi 14–16 Uhr, Fr 9–11 Uhr, SR 404, Eckerstr. 1 |
| | |
Übungen: | 2-stündig |
| | |
Tutorium: | Nina Frohn |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/ziegler/
veranstaltungen/ws09-modell1.html |
| | |
| |
Inhalt:
Die Modelltheorie untersucht den Zusammenhang zwischen formalen Eigenschaften einer
Theorie T erster Stufe und den algebraischen Eigenschaften ihrer Modelle.
Die Theorie der algebraisch abgeschlossenen Körper z.B. hat Quantorenelimination: jede Formel
ist äquivalent zu einer quantorenfreien Formel. Diese für die algebraische Geometrie wichtige
Eigenschaft läßt sich mit Hilfe des Quantoreneliminationkriteriums leicht der Modellklasse
ansehen.
Eine Theorie heißt 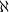 0–kategorisch, wenn alle Modelle der Mächtigkeit
0–kategorisch, wenn alle Modelle der Mächtigkeit 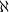 0 (d.h. die abzählbaren
Modelle) isomorph sind. Hauptbeispiel: Die Theorie der dichten linearen Ordnungen. Wir
werden den Satz von Ryll-Nardzewski beweisen: T ist genau dann
0 (d.h. die abzählbaren
Modelle) isomorph sind. Hauptbeispiel: Die Theorie der dichten linearen Ordnungen. Wir
werden den Satz von Ryll-Nardzewski beweisen: T ist genau dann 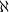 0-kategorisch, wenn es für
jedes n bis auf T-Äquivalenz nur endlich viele Formeln in den Variablen x1,…,xn gibt.
0-kategorisch, wenn es für
jedes n bis auf T-Äquivalenz nur endlich viele Formeln in den Variablen x1,…,xn gibt.
Der viel tiefer liegende Satz von Baldwin–Lachlan charakterisiert die 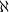 1-kategorischen Theorien.
Dabei wird eine Strukturtheorie entwickelt, die die Modelle solcher Theorien in ähnlicher Weise
durch eine Dimension bestimmt, wie algebraisch abgeschlossene Körper (das Hauptbeispiel)
durch ihren Transzendenzgrad bestimmt sind.
1-kategorischen Theorien.
Dabei wird eine Strukturtheorie entwickelt, die die Modelle solcher Theorien in ähnlicher Weise
durch eine Dimension bestimmt, wie algebraisch abgeschlossene Körper (das Hauptbeispiel)
durch ihren Transzendenzgrad bestimmt sind.
Literatur:
- Tent Ziegler Model Theory. Erscheint im Herbst 2009
- Ziegler Modelltheorie I (Skript)
(http://sunpool.mathematik.uni-freiburg.de/home/ziegler/skripte/modell1.pdf)
- D. Marker Model Theory
- W. Hodges A Shorter Model Theory
Typisches Semester: | 5. Semester |
Studienschwerpunkt: | Reine Mathematik, Mathematische Logik |
Nützliche Vorkenntnisse: | Mathematische Logik |
Folgeveranstaltungen: | Vorlesung Stabilitätstheorie, Seminar Modelltheorie |
Sprechstunde Dozent: | n.V., Zi. 408, Eckerstr. 1; Terminvereinbarung unter Tel. 5602 |
| |
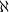 0–kategorisch, wenn alle Modelle der Mächtigkeit
0–kategorisch, wenn alle Modelle der Mächtigkeit 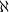 0 (d.h. die abzählbaren
Modelle) isomorph sind. Hauptbeispiel: Die Theorie der dichten linearen Ordnungen. Wir
werden den Satz von Ryll-Nardzewski beweisen: T ist genau dann
0 (d.h. die abzählbaren
Modelle) isomorph sind. Hauptbeispiel: Die Theorie der dichten linearen Ordnungen. Wir
werden den Satz von Ryll-Nardzewski beweisen: T ist genau dann 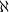 0-kategorisch, wenn es für
jedes n bis auf T-Äquivalenz nur endlich viele Formeln in den Variablen x1,…,xn gibt.
0-kategorisch, wenn es für
jedes n bis auf T-Äquivalenz nur endlich viele Formeln in den Variablen x1,…,xn gibt.