[prev] [prev-tail] [tail] [up]

1.20 Komplexe Geometrie und Kähler-Einstein-Metriken

Vorlesung:

Komplexe Geometrie und Kähler-Einstein-
Metriken

  

Dozent:

PD Ph.D. M. Simon

  

Zeit/Ort:

Mo 14–16 Uhr, SR 127, Eckerstr. 1

  

Übungen:

2-std. n.V.

  

Tutorium:

F. Link

  

Inhalt:
In dieser Vorlesung beschäftigen wir uns mit der Frage: für eine gegebene komplexe Mannigfaltigkeit, existiert eine Kähler-Einstein-Metrik (KEM)? Eine Metrik g auf einer komplexen Mannigfaltigkeit (M,J) ist eine KEM, falls

(M,J,g) Kähler ist, und

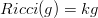
Ricci (g) = kg
für eine Konstante k (wobei hier Ricci(g) die Ricci-Krümmung von g ist).

Die Existenz einer KEM hängt stark von der Topologie und der Struktur der Mannigfaltigkeit ab. Wir präsentieren Bedingungen, die gewährleisten, dass eine KEM existiert, und untersuchen Beispiele für die keine KEM existiert.

Die Vorlesung wird mit einer Einführung in die komplexe und Kähler-Geometrie anfangen. Die Hauptsätze, die wir beweisen, kommen in dem Buch [1] von G. Tian vor.

Literatur:

  1. G. Tian, Canonical Metrics in Kähler Geometry, Lectures in Math., ETH Zürich, Birkhäuser 2000

Typisches Semester:

ab 6. Semester

Studienschwerpunkt:

Reine Mathematik

Notwendige Vorkenntnisse:

Partielle Differentialgleichungen, Differentialgeometrie

Sprechstunde Dozent:

Mi 11:15–12:15 Uhr, Zi. 214, Eckerstr. 1

[prev] [prev-tail] [front] [up]