[next] [prev] [prev-tail] [tail] [up]

1.17 Theorie und Numerik geometrischer partieller Differentialgleichungen

Vorlesung:

Theorie und Numerik geometrischer
partieller Differentialgleichungen

  

Dozent:

Prof. Dr. Gerhard Dziuk

  

Zeit/Ort:

Mi 11–13 Uhr, SR 226, Hermann-Herder-Str. 10

  

Übungen:

14-tgl., zweistündig

  

Tutorium:

Dipl.-Phys. Hans Fritz

  

Inhalt:

Geometrische Differentialgleichungen sind partielle Differentialgleichungen, die geometrische Terme wie zum Beispiel die mittlere Krümmung einer Fläche enthalten. Das einfachste Beispiel einer solchen Gleichung ist die Minimalflächengleichung

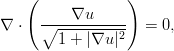
( ) ∇u ∇ ⋅ ∘----------- = 0, 1 + |∇u |2
welche die Tatsache beschreibt, dass die Fläche {(x,u(x))|x ∈ G} mittlere Krümmung Null hat. Typisch für geometrische Differentialgleichungen ist, dass sie einerseits stark nichtlinear sind und andererseits meist in nicht reflexiven Räumen gestellt sind. Dies sind besondere Schwierigkeiten für Analysis und Numerische Analysis.

Geometrische Differentialgleichungen treten außer in der Differentialgeometrie in vielen Anwendungen auf. Beispiele sind Probleme mit Phasenübergängen wie das Wachsen eines Kristalls, die Modellierung von Zellmembranen oder die Bildverarbeitung. Während der Vorlesung werden wir uns die Modellierung, die Analysis und die Numerik solcher Beispiele ansehen.

Wir werden mit dem Modellfall der Berechnung von Flächen vorgeschriebener mittlerer Krümmung beginnen. Außerdem werden wir Differentialgleichungen auf gegebenen Flächen mit der Finite Elemente Methode lösen. Danach werden wir uns mit dynamischen geometrischen Differentialgleichungen befassen, bei denen es um bewegte Flächen geht.

Literatur:

  1. K. Deckelnick, G. Dziuk, C. M. Elliott: Computation of geometric partial differential equations and mean curvature flow. Acta Numerica 2005, 139–232 (2005).
  2. E. Giusti: Minimal Surfaces and Functions of Bounded Variation (1984).

Typisches Semester:

7. Semester

Studienschwerpunkt:

Angewandte Mathematik

Notwendige Vorkenntnisse:

Theorie und Numerik partieller Differentialgleichungen I, II

Sprechstunde Dozent:

Mittwoch 14–15 Uhr, Raum 209, HH-Str. 10 und n. V.

Sprechstunde Assistent:

Dienstag 11–12 Uhr, Raum 211, HH-Str. 10 und n. V.

[next] [prev] [prev-tail] [front] [up]