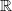[next] [prev] [prev-tail] [tail] [up]

1.2 Analysis III

Vorlesung:

Analysis III

  

Dozent:

Prof. Dr. Ernst Kuwert

  

Zeit/Ort:

Mo 11–13, Fr 9–11/HS Rundbau, Albertstr. 21a

  

Übungen:

2-st. n. V.

  

Tutorium:

Achim Windel

  

Web-Seite:

home.mathematik.uni-freiburg.de/analysis/AnaIII/

  

Inhalt:

Gegenstand der Vorlesung ist die Maß– und Integrationstheorie nach Lebesgue. Es wird ein abstrakter Aufbau der Maßtheorie vorgestellt, der in etwa dem Buch von Elstrodt folgt. Die Definition und Berechnung von Volumen und Integral im 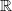ℝn werden dabei ebenfalls ausführlich behandelt. Insbesondere werden Oberflächenintegrale eingeführt und der Integralsatz von Gauß bewiesen. Wenn die Zeit reicht, soll auch die Fouriertransformation diskutiert werden.

Der Stoff der Vorlesung ist für eine Vertiefung in den Gebieten Analysis, Angewandte Mathematik, Stochastik und Geometrie relevant. Auch für Studierende der Physik kann der Inhalt von Interesse sein.

Literatur:

  1. J. Elstrodt: Maß– und Integrationstheorie, 2. Auflage, Springer 1999
  2. H. Amann & J. Escher: Analysis III, Birkhäuser 2001

Typisches Semester:

ab 3. Semester

Studienschwerpunkt:

Analysis, Angewandte Mathematik, Stochastik, Geometrie

Notwendige Vorkenntnisse:

Analysis I, II und Lineare Algebra I

Nützliche Vorkenntnisse:

Lineare Algebra II

Sprechstunde Dozent:

Freitag 11:15–12:15

Sprechstunde Assistent:

Mittwoch 11:00–12:00

[next] [prev] [prev-tail] [front] [up]