Lehrveranstaltungen
1. Vorlesungen
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Stochastik (2. Teil) (B.Sc. und 2-Hf.-B.) |
| | |
Dozent: | Prof. Dr. Peter Pfaffelhuber |
| | |
Zeit/Ort: | Fr 10–11 bzw. Fr. 11–12 Uhr; asynchrones, digitales
Angebot |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | Jakob Stiefel |
| | |
Web-Seite: | https://ilias.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
Erstmalig wird im Sommersemester 2021 der zweite Teil der Vorlesung Stochastik in zwei
inhaltlich unterschiedlichen Parallelen angeboten. Beide Vorlesungen sind sowohl im
B.Sc.-Studiengang als auch im 2-Hf.-B.-Studiengang voll anrechenbar. Beide Parallelen
beschäftigen sich mit grundlegenden Fragen der Mathematischen Statistik.
In der Vorlesung für B.Sc. wird speziell auf Inhalte, die auf eine weitere Beschäftigung mit
Mathematischer Statistik hinführen, eingegangen. Stichworte sind Entscheidungstheorie,
Suffizienz, Exponentialfamilie, Schätzprobleme, Testprobleme.
In der Vorlesung für 2-Hf.-B. wird eher auf schulrelevante Themen eingegangen. Stichwort sind
Punktschätzer, die Rolle der Normalverteilung, Intervallschätzer, statistische Tests.
Für die Vorlesung für 2-Hf.-B. wird eine eigene Praktische Übung angeboten, die jedoch nur von
Hörern dieser Parallele im Sommersemester 2021 belegt werden kann. Alle anderen
Interessenten für die Praktischen Übungen belegen die regelmäßig angebotenen Praktischen
Übungen.
Die Vorlesung wird online in asynchroner Form stattfinden. Weitere organisatorische Details
(Format, Tutorate, Fragestunden zu den Vorlesungen etc.) entnehmen Sie bitte kurzfristig den
entsprechend eingerichteten ILIAS-Seiten.______________________________________________________________
Verwendbarkeit: | siehe Text |
Notwendige Vorkenntnisse: | Erster Teil der Stochastik-Vorlesung, Analysis 1 |
Folgeveranstaltungen: | B.Sc.: Wahrscheinlichkeitstheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
In der Vorlesung soll eine Einführung in die Elementargeometrie im euklidischen und
nicht-euklidischen Raum und seine mathematischen Grundlagen gegeben werden. Wir behandeln
im Einzelnen dazu die Themen der Axiomatik, Isometrien-Bewegungsgruppe und Trigonometrie
der euklidischen, hyperbolischen und sphärischen Geometrie. Im weiteren Verlauf schauen wir
uns die Geschichte des fünften Euklidischen Axioms (und die Versuche, es los zu werden) an,
diskutieren die kontraintuitiven Ergebnisse der daraus hervorgegangen hyperbolischen Geometrie
(z.B. existieren dort Dreiecke mit der Innenwinkelsumme Null). Ferner geben wir eine
Einführung in die Projektive Geometrie und betrachten Polygone, Polyeder und deren
Eigenschaften.
Literatur:
-
1.)
- C. Bär: Elementare Differentialgeometrie (2. Auflage), De Gruyter, 2010.
-
2.)
- M. Berger: Geometry I (Corrected Third Printing), Springer Universitext, 2004
-
3.)
- R. Hartshorne: Geometry: Euclid and beyond, Springer, 2000.
-
4.)
- H. Knörrer: Geometrie (2. Auflage), Springer Vieweg, 2006.
___________________________________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Pflichtmodul im 2-Hf-Bachelor; Wahlpflichtmodul im B.Sc.
Nicht verwendbar in den Master-Studiengängen. |
Notwendige Vorkenntnisse: | Lineare Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Lie-Gruppen sind glatte Mannigfaltigkeiten, die eine Gruppenstruktur tragen, und zwar so, dass
die Verknüpfung und die Inversenbildung glatte Abbildungen sind. Zu den einfachsten Beispielen
gehören die GLn(ℝ) und die SU(n). Auf dem Tangentialraum in der Identität solch einer
Lie-Gruppe erhält man in natürlicher Weise die Struktur einer Lie-Algebra. Damit gehört die
Theorie der Lie-Gruppen und Lie-Algebren zu den klassischen Themen der Differentialgeometrie,
die weitreichende Anwendungen in der Geometrie und auch in der mathematischen Physik
haben.
Als einfachste Bausteine der Lie-Algebren kann man die sogenannten einfachen Lie-Algebren
ansehen. Die endlich-dimensionalen einfachen Lie-Algebren über ℂ kann man mit
kombinatorischen Mitteln klassifizieren. Sie werden mit den Typen A, B, C, D, E, F, G
bezeichnet, wobei die Typen A, D, E eine Sonderstellung einnehmen. Die kombinatorischen
Daten lassen sich besonders schön mittels der sogenannten Dynkin-Diagramme festhalten.
Im ersten Teil der Vorlesung werden die Grundlagen der Theorie der Lie-Algebren
erarbeitet und die Klassifikation der endlich-dimensionalen einfachen Lie-Algebren über ℂ
vorgestellt.
Die Dynkin-Diagramme tauchen in erstaunlich vielen anderen Bereichen der Mathematik immer
wieder auf. So klassifizieren die Dynkin-Diagramme der Typen A, D, E auch die sogenannten
einfachen Singularitäten, denen wir uns im zweiten Teil der Vorlesung zuwenden werden.
Schließlich soll in einem dritten Teil der Vorlesung noch gezeigt werden, wie die beiden vorher
untersuchten, scheinbar grundverschiedenen ADE-klassifizierten Strukturen mit einander
zusammenhängen.
Literatur:
-
1.)
- R. Carter, G. Segal, I. Macdonald, Lectures on Lie Groups and Lie Algebras, Cambridge
University Press 1995
-
2.)
- W. Ebeling, Funktionentheorie, Differentialtopologie und Singularitäten, Vieweg 2001
-
3.)
- A.W. Knapp, Lie Groups Beyond an Introduction, Birkhäuser, 1996
-
4.)
- P. Slodowy, Simple Singularities and Simple Algebraic Groups, Springer 1980
___________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Differentialgeometrie I |
Nützliche Vorkenntnisse: | Funktionentheorie, Differentialtopologie, Kommutative
Algebra, Einführung in die algebraische Geometrie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Elementare Differentialgeometrie |
| | |
Dozent: | Prof. Dr. Ernst Kuwert |
| | |
Zeit/Ort: | 4-std.: digitales Angebot |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | Dr. Marius Müller |
| | |
| |
_______________________________________________________________
Inhalt:
Es geht um die Geometrie von Kurven und Flächen im ℝn. Im Vordergrund steht dabei die
Frage, was die Krümmung einer Kurve bzw. Fläche ist und welche geometrische Bedeutung sie
für die Kurve bzw. Fläche als Ganzes hat. Entlang der Theorie werden zahlreiche Beispiele
behandelt. Gegen Ende der Vorlesung werden abstrakte, also nicht eingebettete Flächen
betrachtet, zum Beispiel die die hyperbolische Ebene.
Die Vorlesung ist für Studierende für Studieende im Bachelor Mathematik und im polyvalenten
Bachelor gleichermaßen geeignet, und sie ist bei Verteifung in den Bereichen Analysis, Geometrie
und Angewandte Mathematik relevant.
Literatur:
-
1.)
- E. Kuwert: Elementare Differentialgeometrie, Skript 2018,
http://home.mathematik.uni-freiburg.de/analysis/ElDiffGeo18/skript.pdf
-
2.)
- C. Bär: Elementare Differentialgeometrie, de Gruyter 2001.
-
3.)
- M. P. do Carmo: Differential Geometry of Curves and Surfaces, Prentice Hall 1976.
-
4.)
- W. Klingenberg: Eine Vorlesung über Differentialgeometrie, Springer Verlag 1973.
_____________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie II |
Notwendige Vorkenntnisse: | Grundvorlesungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Diese Vorlesung entwickelt die Zahlentheorie auf Grundlage der Algebra und Zahlentheorie
Vorlesung weiter. Sie ist unabhängig von der Vorlesung Algebraische Zahlentheorie, d.h.
man kann beide Vorlesungen (in beliebiger Reihenfolge) hören, oder auch nur eine
davon.
Grundkenntnisse in der Funktionentheorie wären wünschenswert, aber wir benötigen nur wenig
und können dies bei Bedarf auch einflechten (oder man hört es parallel).
Ausgangspunkt der Vorlesung ist das Problem, für gewisse Gleichungen ganzzahlige oder
rationale Lösungen zu finden, also z.B. die Frage: Sei n ≥ 2. Welche x,y,z ∈ ℚ lösen die
Gleichung

Diese Ausgangsfrage ist fast identisch zum Ausgangsproblem der Vorlesung Algebraische
Zahlentheorie, allerdings werden wir die Fragestellung mit völlig anderen Methoden angehen.
Auf dem Weg dahin werden wir elliptische Kurven, p-adische Methoden, Modulformen und
Galoiskohomologie kennenlernen. Außerdem werden uns eine Reihe bislang ungelöster
mathematischer Probleme begegnen, und einige, die erst in den letzten 30 Jahren gelöst
wurden.___________________________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik, Kategorie III |
Notwendige Vorkenntnisse: | Algebra und Zahlentheorie |
Nützliche Vorkenntnisse: | Funktionentheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Diese Vorlesung überträgt Begriffe der linearen Algebra auf normierte und topologische
Vektorräume und stetige lineare Abbildungen zwischen ihnen. Dabei spielen Begriffe wie
Konvergenz, Vollständigkeit, Beschränktheit und Kompaktheit eine große Rolle.
Typische Beispiele solcher Vektorräume sind Sobolev-Räume, das heißt, Räume von
Funktionen, die im schwachen Sinne differenzierbar sind, und deren Ableitungen eine
Integrabilitätsbedingung erfüllen. Zu den interessanteren linearen Abbildungen zwischen solchen
Räumen gehören Differential- und Integraloperatoren. Damit bildet Funktionalanalysis eine
wichtige Grundlage für das Studium von Differentialgleichungen in Analysis, Geometrie und
Numerik, aber beispielsweise auch für die Quantenmechanik.
In der Vorlesung werden zum einen abstrakte Konzepte wie Dualräume, Vervollständigung,
stetige und kompakte lineare Abbildungen eingeführt. Zum anderen wollen wir auch Beispiele
und Anwendungen kennenlernen.__________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine oder Angewandte Mathematik; Kategorie II |
Notwendige Vorkenntnisse: | Lineare Algebra, Analysis |
Nützliche Vorkenntnisse: | Analysis III |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Diese Vorlesung beschäftigt sich mit der Theorie der komplex differenzierbaren komplexwertigen
Funktionen einer komplexen Veränderlichen. Sie werden lernen, daß diese viel starrer sind als die
differenzierbaren reellwertigen Funktionen einer reellen Veränderlichen und in ihren
Eigenschaften eher Polynomfunktionen ähneln. Die Funktionentheorie ist grundlegend für
das Studium weiter Teile der Mathematik, insbesondere der Zahlentheorie und der
algebraischen Geometrie, und ihre Anwendungen reichen bis in die Wahrscheinlichkeitstheorie,
Funktionalanalysis und Mathematische Physik.
Literatur:
-
1.)
- Fischer-Lieb: Funktionentheorie
-
2.)
- Freitag-Busam: Funktionentheorie 1
-
3.)
- Jänich: Funktionentheorie
-
4.)
- Soergel, Skript zur Funktionentheorie
http://home.mathematik.uni-freiburg.de/soergel/Skripten/XXFT1.pdf
____________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie II |
Notwendige Vorkenntnisse: | Analysis 1&2, Lineare Algebra 1&2 |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Kommutative Algebra und Einführung in die
algebraische Geometrie |
| | |
Dozent: | Prof. Dr. Stefan Kebekus |
| | |
Zeit/Ort: | Di, Do, 10–12 Uhr, voraussichtlich online |
| | |
Übungen: | 2-std., n.V. |
| | |
Tutorium: | Andreas Demleitner |
| | |
Web-Seite: | https://cplx.vm.uni-freiburg.de/de/teaching/ |
| | |
| |
_______________________________________________________________
Inhalt:
Kommutative Algebra ist eine allgemeinere Version der linearen Algebra über kommutativen
Ringen statt über Körpern. Der Begriff des Moduls ersetzt den des Vektorraums. Weite Teile von
Geometrie und Analysis verwenden diese Konzepte, die Hauptanwendungsgebiet sind jedoch
Zahlentheorie und algebraische Geometrie. Wir werden die formale Theorie daher mit einem der
wichtigsten Anwendungsfälle kombinieren und gleichzeitig die Grundlagen der algebraischen
Geometrie erarbeiten.
Algebraische Varietäten sind Lösungsmengen polynomialer Gleichungssysteme. Dies sind
geometrische Objekte, die wir mit algebraischen Methoden studieren. Die Theorie der
affinen Varietäten entspricht der Theorie der Ideale in Polynomringen mit endlich
vielen Variablen. Damit ist der Bogen zur kommutativen Algebra gespannt. Parallel
zur Vorlesung wird von uns ein Seminar angeboten, das den Bezug zur Geometrie
vertieft.
Literatur:
-
1.)
- Atiyah, MacDonald: Introduction to commutative algebra
-
2.)
- Mumford: The red book of varieties and schemes
-
3.)
- Shafarevich: Basic algebraic geometry
-
4.)
- Eisenbud: Commutative Algebra with a View Toward Algebraic Geometry
-
5.)
- Fulton: Algebraic Curves, http://www.math.lsa.umich.edu/wfulton/CurveBook.pdf
____
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik, Kategorie III |
Notwendige Vorkenntnisse: | Vorlesung Lineare Algebra I und II |
Nützliche Vorkenntnisse: | Vorlesung Algebra und Zahlentheorie |
Folgeveranstaltungen: | Wir planen, im WS 2021/22 weiterführende Veranstaltungen
zur Algebraischen Geometrie anzubieten |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Mathematische Logik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Dies ist eine Einführung in die mathematische Logik. Wir werden den Begriff eines
mathematischen Beweises präzisieren. Für den festgelegten Beweisbegriff beantworten wir dann
folgende Fragen: Von welchen (nicht beweisbaren) Grundprinzipien geht man aus? Kann man
das Nachprüfen oder gar das Finden von Beweisen geeigneten Computern überlassen?
Gegenstände der Vorlesung sind der Gödel’sche Vollständigkeitssatz und die Gödel’schen
Unvollständigkeitssätze und die ersten Grundlagen der Rekursionstheorie, der Modelltheorie und
der Mengenlehre.
Literatur:
-
1.)
- H.-D. Ebbinghaus, J. Flum, W. Thomas, Einführung in die mathematische Logik, Spektrum
Verlag, 2007.
-
2.)
- Martin Hils and François Loeser, A First Journey Through Logic, Student Mathematical
Library vol. 89, American Mathematical Society, Providence, RI, 2019.
-
3.)
- Peter G. Hinman. Fundamentals of Mathematical Logic. A K Peters, Ltd., Wellesley, MA,
2005. xvi+878 pp
-
4.)
- Joseph R. Shoenfield, Joseph, Mathematical Logic. Reprint of the 1973 second printing.
Association for Symbolic Logic, Urbana, IL; A K Peters, Ltd., Natick, MA, 2001.
-
5.)
- Martin Ziegler, Vorlesungsskript „Mathematische Logik”.
-
6.)
- Martin Ziegler, Mathematische Logik, 2. Auflage, Birkhäuser, 2017.
_________________________________________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie II |
Notwendige Vorkenntnisse: | mindestens eine Grundvorlesungen |
Nützliche Vorkenntnisse: | drei Grundvorlesungen |
Folgeveranstaltungen: | Mengenlehre, Modelltheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Mathematische Logik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Die Vorlesung besteht aus einer Einführung in die Modelltheorie, ein Teilgebiet der
Mathematischen Logik. Modelltheorie untersucht zum einen, wie sich die Form der
Axiomatisierung auf eine Klasse von Strukturen auswirkt (zum Beispiel lässt sich etwas genau
dann durch Allquantoren ausdrücken, wenn die zugehörige Modellklasse unter Unterstrukturen
abgeschlossen ist). Zum andern versucht die Modelltheorie in schönen Fällen die Modelle eines
Axiomensystems näher zu beschreiben. Ziel sind die Sätze von Morley und Baldwin-Lachlan:
Wenn eine vollständige Theorie in einer überabzählbaren Kardinalität bis auf Isomorphie
nur ein einziges Modell hat, dann gilt dies in allen überabzählbaren Kardinalitäten,
und die Modelle lassen sich ähnlich wie Vektorräume durch Basen und Dimension
beschreiben.
Die Vorlesung setzt einige Kenntnisse aus der formalen Logik voraus (prädikatenlogische
Sprache, Auswertung von Formeln in Modellen, unendliche Kardinalitäten), die kurz wiederholt
werden. Sie kann ohne vorausgehende „Mathematische Logik“ gehört werden, wenn man bereit
ist, sich diese Logik-Grundlagen im Selbststudium anzueignen. Beispiele kommen oft aus der
Algebra.
Wenn die Infektionslage es zulässt, soll Vorlesung in Präsenz stattfinden, alternativ live über
BigBlueButton. Nähere Informationen kurzfristig auf der Webseite der Vorlesung!
Literatur:
-
1.)
- M. Ziegler: Skript „Modelltheorie“, 2001.
https://home.mathematik.uni-freiburg.de/ziegler/Skripte.html
-
2.)
- K. Tent, M. Ziegler: “A course in model theory”, Association of Symbolic Logic 2012.
_______
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Grundvorlesungen und etwas Logik |
Nützliche Vorkenntnisse: | Mathematische Logik, Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Numerical Optimal Control in Science and
Engineering |
| | |
Dozent: | Prof. Dr. Moritz Diehl |
| | |
Zeit/Ort: | online lecture |
| | |
Übungen: | (ggf. unregelmäßig) Fr 10–12 Uhr, SR 226,
Hermann-Herder-Str. 10 |
| | |
Tutorium: | M.Sc. Florian Messerer |
| | |
Web-Seite: | http://syscop.de/teaching |
| | |
| |
_______________________________________________________________
Content:
The aim of the course is to give an introduction into numerical methods for the solution of
optimal control problems in science and engineering. The focus is on both discrete time and
continuous time optimal control in continuous state spaces. It is intended for a mixed audience of
students from mathematics, engineering and computer science.
The course covers the following topics: Introduction to Dynamic Systems and Optimization
- Rehearsal of Numerical Optimization
- Rehearsal of Parameter Estimation
- Discrete Time Optimal Control
- Dynamic Programming
- Continuous Time Optimal Control
- Numerical Simulation Methods
- Hamilton–Jacobi–Bellmann Equation
- Pontryagin and the Indirect Approach
- Direct Optimal Control
- Differential Algebraic Equations
- Periodic Optimal Control
- Real-Time Optimization for Model Predictive Control.
The lecture is accompanied by intensive weekly computer exercises based on MATLAB
(6 ECTS) and an optional project (3 ECTS). The project consists in the formulation and
implementation of a self-chosen optimal control problem and numerical solution method,
resulting in documented computer code, a project report, and a public presentation.
Literature:
-
1.)
- Manuscript Numerical Optimal Control by M. Diehl and S. Gros.
-
2.)
- L.T. Biegler: Nonlinear Programming, SIAM, 2010.
-
3.)
- J. Betts: Practical Methods for Optimal Control and Estimation Using Nonlinear
Programming, SIAM, 2010.
___________________________________________________________
ECTS-Punkte: | nur Vorlesung und Übungen: 6 Punkte; mit Projekt: 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Analysis I und II, Lineare Algebra I und II |
Nützliche Vorkenntnisse: | Einführung in
die Numerik, Gewöhnliche Differentialgleichungen, Numerical
Optimization |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Kurssprache ist Englisch |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Partielle Differentialgleichungen II:
Various Topics |
| | |
Dozent: | Prof. Dr. Guofang Wang |
| | |
Zeit/Ort: | asynchrones digitales Angebot, Mo, Mi |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | M.Sc. Jan Metsch |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/wang/ |
| | |
| |
_______________________________________________________________
Inhalt:
Die Vorlesung ist eine Vertiefung der Vorlesung “Einführung in PDE”, nicht eine der PDE I. In
der Vorlesung untersuchen wir die sogenannte Liouville-Gleichung
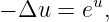 die
in vielen mathematischen, physikalischen und auch geometrischen Problemen auftreten. Wir
untersuchen sowie die Klassifikation und die Existenz ihrer Lösungen, als auch die
Kompaktheit der Menge von Lösungen. Aber am Anfang lernen wir die passende
Grundlage der nicht-linearen PDE und Variationsrechnung, damit die Vorlesung vollständig
ist.
die
in vielen mathematischen, physikalischen und auch geometrischen Problemen auftreten. Wir
untersuchen sowie die Klassifikation und die Existenz ihrer Lösungen, als auch die
Kompaktheit der Menge von Lösungen. Aber am Anfang lernen wir die passende
Grundlage der nicht-linearen PDE und Variationsrechnung, damit die Vorlesung vollständig
ist.
Literatur:
-
1.)
- Skript
_________________________________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Einführung in PDE, oder Einführung in Theorie und Numerik
PDE |
Nützliche Vorkenntnisse: | Funktionalanalysis |
Folgeveranstaltungen: | Lesekurs |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Singuläre Integraloperatoren |
| | |
Dozent: | Prof. Dr. M. Růžička |
| | |
Zeit/Ort: | Di, Do 10–12 Uhr, BBB-Raum vRuzicka |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | A. Kaltenbach |
| | |
| |
_______________________________________________________________
Inhalt:
Singuläre Integraloperatoren sind wichtige Werkzeuge in der harmonischen Analysis und in der
Theorie partieller Differentialgleichungen. Stellt man z.B. die Lösung des Laplace Problems in
ℝ3 mit Hilfe der Faltung des Newton–Potentials dar, so ergibt die Darstellung der
zweiten Ableitungen einen singulären Integraloperator. Diese Operatoren entstehen im
allgemeinen durch Faltung mit einem singulären Kern, der nicht in L2 ist. In der Vorlesung
wird eine Einführung in die klassische Theorie singulärer Operatoren in Lp–Räumen
gegeben (Maximal-Funktion, Überdeckungssätze, Marcinkiewicz Interpolationstheorem,
Calderon-Zygmund-Abschätzungen).
Literatur:
-
1.)
- Elias M. Stein, Singular Integrals and Differentiability Properties of -functions, Princeton
University Press, Princeton, N.J., 1970.
-
2.)
- Elias M. Stein, Harmonix Analysis: Real-variable Methods, Orthogonality and Oscillatory
Integrals, Princeton University Press, 1993.
-
3.)
- A. P. Calderón and A. Zygmund, On Singular Integrals, Amer. J. Math. 78 (1956), 289–309.
-
4.)
- Ronald R. Coifman and Yves Meyer, Au delà des opérateurs pseudo-différentiels, Société
Mathématique de France, Paris, 1978.
______________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Grundvorlesungen Analysis, Lineare Algebra |
Nützliche Vorkenntnisse: | Einführung in Theorie und Numerik partieller
Differentialgleichungen oder Funktionalanalysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Das Studium von zufälliger Matrizen und insbesondere von Eigenschaften ihrer Eigenwerte ist
entscheidend aus der statistischen Datenanalyse heraus motiviert. Von fundamentaler Bedeutung
ist hier die empirische Kovarianzmatrix – eine symmetrische, positiv-semidefinite Zufallsmatrix.
In der hochdimensionalen Asymptotik, falls Stichprobenumfang und Dimension von derselben
Größenordnung sind, treten eine Vielzahl spannender wahrscheinlichkeitstheoretischer
Phänomene auf. Im Zentrum der Vorlesung stehen Resultate, die unter Momentenbedingungen
an die Zufallsvariablen bewiesen werden. Beispielsweise behandeln wir das Wignersche
Halbkreisgesetz, die Marcenko-Pastur-Verteilung, zentrale Grenzwertsätze für lineare
Spektralstatistiken, Konvergenz der extremalen Eigenwerte und die Tracy-Widom-Verteilung
sowie den sogenannten empirische Spektralprozess.
Literatur:
-
1.)
- Wird in der Vorlesung bekanntgegeben.
_________________________________________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Im Anschluss an die Vorlesung stochastische Prozesse befasst sich diese Vorlesung ausführlich
mit finanzmathematischen Fragestellungen. Zu Beginn betrachten wir Fundamentalsätze
zur Freiheit von Arbitrage. Danach widmen wir uns einer Auswahl weiterführender
Themen wie Zinsmodellierung, Modellierung von Aktien- und Optionspreisen mit
stochastischer Volatilität, Kreditrisikomodellierung, Bewertung amerikanischer Optionen, und
Modellrisiko.
Literatur:
-
1.)
- Wird in der Vorlesung bekanntgegeben.
_________________________________________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Stochastische Prozesse |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Mathematische Logik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Gruppen, die keine nicht trivialen Normalteiler enthalten, heißen einfache Gruppen. Ähnlich wie
Primzahlen für die natürlichen Zahlen, bilden einfache Gruppen die Bausteine für endliche
Gruppen. Man sieht leicht, dass abelsche endliche einfache Gruppen zyklisch sind.
Nicht abelsche Beispiele sind alternierende Gruppen sowie die Gruppen vom Lie-Typ.
Die Klassifikation von endlichen einfachen Gruppen geht weit über den Rahmen dieses
Kurses hinaus. Wir werden jedoch einige der wiederkehrenden Ideen der Klassifikation
veranschaulichen und insbesondere das folgende Ergebnis von Brauer und Fowler beweisen:
Theorem. Sei G eine einfache endliche Gruppe von gerader Ordnung und g ein element von
Ordnung 2. Dann gilt |G|≤ (|CG(g)|2)!.
Diesen Theorem hatte besonders großen Einfluss auf die Klassifikation endlicher einfacher
Gruppe, da es suggeriert, dass diese durch Untersuchung der Zentralisatoren von Elementen von
zweiter Ordnung klassifiziert werden könnten.
Literatur:
-
1.)
- J. S. Rose, A course on Group Theory, Cambridge University Press, 1978
-
2.)
- J. J. Rotman, An introduction to the Theory of Groups, Springer-Verlag, 1999
-
3.)
- R. Solomon, A brief history of the classification of the finite simple groups, Bulletin American
Mathematical Society 38 (2001), no. 3, 315–352
__________________________________________________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Algebra und Zahlentheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Mathematische Logik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Content:
Paul Cohen famously devised the method of forcing to prove that the statement 2ℵ0 = ℵ
1,
commonly known as the continuum hypothesis, is independent of the standard Zermelo–Fraenkel
axioms (abbreviated ZFC), which are the basic assumptions used by most working
mathematicians. However, there are many natural mathematical questions that are not settled
by ZFC and require the use of additional assumptions. These typically come in the form of
large cardinals axioms. Modern research in large cardinals has exhibited a complex
interrelationship with forcing axioms, determinacy axioms, and the topology of the real
line.
This course will introduce large cardinals, their basic properties, and their interplay with the
method of forcing. We will begin by covering the measure problem and classical motivations for
large cardinals, some model-theoretic characterizations of large cardinals, and Gödel’s inner
model L of constructible sets—a useful tool for showing when certain large cardinals are
necessary for resolving a given question. We will then explore significant examples of the
application of large cardinals. Possible topics include: the independence of the Kurepa
Hypothesis and the equiconsistency of its failure with the existence of an inaccessible cardinal;
the independence of the Tree Property at ℵ2 and its equiconsistency with the existence of a
weakly compact cardinal; and Solovay’s model of set theory in which all sets of real numbers are
Lebesgue-measurable (in which the consistency of an inaccessible cardinal is provably
necessary).
The course in forcing is strongly recommended as a prerequisite for this one.
Literature:
-
1.)
- Thomas Jech. Set Theory. Perspectives in Mathematical Logic. Springer-Verlag, Berlin,
second edition, 1997.
______________________________________________________________________________________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Mathematische Logik |
Nützliche Vorkenntnisse: | Unabhängigkeitsbeweise |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Es gibt topologische Mannigfaltigkeiten, die keine differenzierbare Struktur tragen können, zum
Beispiel die zweifache Einhängung der dreidimensionalen Poincaré-Sphäre. Auf anderen
topologischen Mannigfaltigkeiten wie der 7-Sphäre existieren verschiedene, nicht diffeomorphe
glatte Strukturen.
In der Vorlesung lernen wir Beispiele und Konstruktionsmethoden für glatte und stückweise
lineare Strukturen auf Mannigfaltigkeiten kennen. Auf der anderen Seite wollen wir auch
Hindernisse für die Existenz solcher Strukturen betrachten, und Invarianten, mit denen man sie
unterscheiden kann.
Literatur:
-
1.)
- Hirsch and Mazur, Smoothings of Piecewise Linear Manifolds, Princeton University Press,
Princeton NJ, 1974
-
2.)
- Kirby and Siebenmann, Foundational Essays on Topological Manifolds, Smoothings, and
Triangulations, Princeton University Press, Princeton NJ, 1977
-
3.)
- Rudyak, Piecewise Linear Structures on Topological Manifolds, World Scientific, New Jersey,
2016
___________________________________________________________________________________________________________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Algebraische Topologie |
Nützliche Vorkenntnisse: | Differentialtopologie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Mathematische Modellierung |
| | |
Dozent: | Prof. Dr. M. Růžička |
| | |
Zeit/Ort: | Do 9–10 Uhr, BBB-Raum vRuzicka |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | A. Kaltenbach |
| | |
| |
_______________________________________________________________
Inhalt:
Als Modelle für viele physikalische Vorgänge, wie z.B. der Bestimmung einer Temperaturverteilung,
der Beschreibung von Schwingungen von Membranen oder von Strömungen von Flüssigkeiten,
treten partielle Differentialgleichungen auf.
In der Vorlesung werden wir diese Gleichungen aus der Sicht der Kontinuumsmechanik herleiten
sowie Grundprinzipien für die Modellierung von Materialeigenschaften kennenlernen.
Literatur:
-
1.)
- Chadwick, Continuum Mechanics, Dover (1999).
_______________________________________________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Grundvorlesungen Analysis, Lineare Algebra |
Nützliche Vorkenntnisse: | Einführung in Theorie und Numerik partieller
Differentialgleichungen oder Funktionalanalysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Vorlesung: | Numerik für Differenzialgleichungen |
| | |
Dozent: | Prof. Dr. Sören Bartels |
| | |
Zeit/Ort: | Durchführung in asynchroner digitaler Form |
| | |
Übungen: | 2-std. n.V. (14-täglich) |
| | |
Tutorium: | M.Sc. Jakob Keck |
| | |
Web-Seite: | http://aam.uni-freiburg.de/agba/lehre/ss21/ndgln |
| | |
| |
_______________________________________________________________
Inhalt:
Differenzialgleichungen sind ein wichtiges mathematisches Werkzeug zur Beschreibung
realer Vorgänge wie beispielsweise der Flugbahn eines Satelliten, der Entwicklung von
Raub- und Beutetierpopulationen oder dem Abkühlen eines Körpers. In der Vorlesung
werden verschiedene mathematische Modelle diskutiert und numerische Verfahren zur
praktischen Lösung gewöhnlicher Differenzialgleichungen der Form y′(t) = f(t,y(t))
untersucht.
Studierende, die die Veranstaltung im M.Sc.- oder M.Ed.-Studiengang nutzen wollen, können Sie
durch eine Projektarbeit und das Praktikum auf 9 ECTS-Punkte aufstocken.
Literatur:
-
1.)
- S. Bartels: Numerik 3x9. Springer, 2016
-
2.)
- R. Plato: Numerische Mathematik kompakt. Vieweg, 2006
-
3.)
- W. Walter: Gewöhnliche Differentialgleichungen: Eine Einführung. Springer, 2000
______________
ECTS-Punkte: | 5 (mit Praktikum und Projektarbeit 6 bzw. 9) Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie II |
Notwendige Vorkenntnisse: | Kenntnisse aus den Pflichtvorlesungen sind ausreichend. |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Die Veranstaltung bietet eine Einführung in die Programmierung mit theoretischen und
praktischen Einheiten. Schwerpunkte der Veranstaltung sind:
- Logische Grundlagen der Programmierung
- Elementares Programmieren in C++
- Funktionsweise eines Prozessors
- Felder, Zeiger, abgeleitete Datentypen, (Datei-)Ein- und -ausgabe
- Algorithmik
- Programmieren und Visualisieren in MATLAB
- Funktionsweise eines Compilers
- Paralleles und objektorientiertes Programmieren
- Aspekte der IT-Kommunikation
Die praktischen Inhalte werden in der Programmiersprache C++ sowie in MATLAB erarbeitet.
Die erworbene Kenntnisse werden anhand von Übungen und Hausaufgaben erprobt und
vertieft.
Literatur:
-
1.)
- S. Bartels, C. Palus, L. Striet: Einführung in die Programmierung (Vorlesungsskript)
-
2.)
- R. Drechsler, A. Fink, J. Stopper: Computer, Springer 2017
-
3.)
- T. Häberlein: Technische Informatik, Springer 2011
-
4.)
- R. Klima, S. Selberherr: Programmieren in C, Springer 2010
-
5.)
- G. Küveler, D. Schwoch: C/C++ für Studium und Beruf, Springer 2017
-
6.)
- D. Logofatu: Einführung in C, Springer 2016
-
7.)
- H. Müller, F. Weichert: Vorkurs Informatik, Springer 2017
-
8.)
- M. von Rimscha, Algorithmen kompakt und verständlich, Springer 2014
-
9.)
- R. Schneeweiß: Moderne C++ Programmierung, Springer 2012
-
10.)
- G. Vossen, K.-U. Witt: Grundkurs Theoretische Informatik, Springer 2016
_______________
ECTS-Punkte: | Als BOK-Kurs über das ZfS 6 Punkte |
Bemerkung: | Der Kurs kann mit gleichen Anforderungen als Praktische
Übung im 2-Hf-Bachelor oder als Modul „Mathematische
Ergänzung“ im M.Ed. (jeweils 3 ECTS-Punkte) verwendet
werden. |
| |
2. Berufsorientierte Veranstaltungen
Mathematisches Institut
SS2021
__________________________________________________________________________________________________________________________________________________________
Veranstaltung: | Lernen durch Lehren |
| | |
Dozent: | Alle Dozentinnen und Dozenten von Vorlesungen |
| | |
Zeit/Ort: | Termin und Ort der Einführungsveranstaltung werden
kurzfristig im Vorlesungsverzeichnis in HISinOne bekannt
gegeben |
| | |
| |
_______________________________________________________________
Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu
Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem
Bachelor- oder M.Sc.–Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor mit
Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um eine
Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige
oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an
die Vorlesung).
Leistungsnachweis:
- Teilnahme an dem Einführungsworkshop. Voraussichtlich etwa zwei halbe Tage; einen
ungefähr in der ersten Vorlesungswoche und einen nach etwa vier Wochen. Näheres
wird rechtzeitig bekanntgegeben.
- Regelmäßige Teilnahme an der Tutorenbesprechung.
- Zwei gegenseitige Tutoratsbesuche
mit einem (oder mehreren) anderen Modulteilnehmer, welcher nach Möglichkeit die
gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten,
und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der
Einführungsveranstaltung).
Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im M.Sc.-Studiengang
absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlbereich (im 2-Hf-Bachelor:
„Optionsbereich“) angerechnet. Im 2-Hf-Bachelor ist es bei Wahl der Lehramtsoption eine über
die 180 geforderter ECTS-Punkte hinausgehende Zusatzleistung. Es handelt sich um eine
Studienleistung, d.h. das Modul wird nicht benotet._________________________________________________
Abteilung für
Didaktik der Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Seminar: | MatheUnterricht = MatheStudium ±x |
| | |
Dozent: | Holger Dietz |
| | |
Zeit/Ort: | Do 10–12 Uhr, SR 404, Ernst-Zermelo-Str. 1 |
| | |
Vorbesprechung: | Termin wird noch bekannt gegeben |
| | |
Teilnehmerliste: | Interessenten tragen sich bitte per E-Mail bei Frau Schuler ein:
didaktik@math.uni-freiburg.de
max. 21 Teilnehmer(innen) da Präsenzveranstaltung, falls Corona
es zulässt |
| | |
Web-Seite: | http://www.mathematik.uni-freiburg.de/didaktik/ |
| | |
| |
_______________________________________________________________
Inhalt:
Als Schüler ahnt man nicht, was es heißt, Mathematik zu studieren. Ähnlich vage ist häufig
die Vorstellung im Studium davon, was es bedeutet, Mathematik in der Schule zu
unterrichten. Dieses Seminar möchte konkrete Aus- bzw. Einblicke in die Praxis des
Mathematikunterrichtens geben und versucht dabei, auf den Erfahrungen z.B. aus dem
Praxissemester aufzubauen.
Ausgewählte Inhalte und Aspekte des Mathematikunterrichts (vom Arbeitsblatt bis zur
Zahlenbereichserweiterung) werden nicht nur vom Standpunkt der Fachwissenschaft, sondern
auch aus Lehrer- und Schülersicht analysiert und hinterfragt. Oft verbergen sich hinter den
mathematisch einfacheren Themen unerwartete didaktische Herausforderungen. Daher soll neben
der Auseinandersetzung mit bestehenden Inhalten und Rahmenbedingungen auch Unterricht
selbst geplant und – wenn möglich – an der Schule durchgeführt werden.
Leistungen im Seminar:
-
1.
- Benotet: Gestaltung und Durchführung einer Seminarsitzung (zu einem mathematikdidaktischen
Schwerpunkt)
-
2.
- Benotet: Konzeption und (anteilige) Durchführung von Mathematik-Unterricht
-
3.
- Bearbeitung von „Hausaufgaben“ wie z.B. Literaturarbeit, Planung von Unterrichtseinstiegen,
Erstellung von Erklärvideos etc. (kann je nach Aufgabenart auch zur Notenbildung mit herangezogen
werden).
___________________________________________________________________________________________________________________________
ECTS-Punkte: | 4 Punkte |
Verwendbarkeit: | Modul Fachdidaktische Entwicklung im Master of Education;
Fachdidaktik-Seminar im Lehramt nach GymPO |
Notwendige Vorkenntnisse: | Grundvorlesungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Diese drei zusammengehörigen Veranstaltungen bereiten auf das Anfertigen einer
empirischen Masterarbeit in der Mathematikdidaktik vor. Das Angebot wird von allen
Professorinnen und Professoren mit mathematikdidaktischen Forschungsprojekten
der Sekundarstufe 1 und 2 gemeinsam konzipiert und von einem dieser Forschenden
durchgeführt. Im Anschluss besteht das Angebot, bei einem/einer dieser Personen eine
fachdidaktische Masterarbeit anzufertigen – meist eingebunden in größere laufende
Forschungsprojekte.
In der ersten Veranstaltung findet eine Einführung in Strategien empirischer fachdidaktischer
Forschung statt (Forschungsfragen, Forschungsstände, Forschungsdesigns). Studierende vertiefen
ihre Fähigkeiten der wissenschaftlichen Recherche und der Bewertung fachdidaktischer
Forschung.
In der zweiten Veranstaltung (im letzten Semesterdrittel) werden die Studierenden durch
konkrete Arbeit mit bestehenden Daten (Interviews, Schülerprodukte, Experimentaldaten) in
zentrale qualitative und quantitative Forschungsmethoden eingeführt.
Die Haupziele des Moduls sind:
- Fähigkeit zur Rezeption mathematikdidaktischer Forschung zur Klärung
praxisrelevanter Fragen,
- Planung einer empirischen mathematikdidaktischen Masterarbeit.
Es wird abgehalten werden als Mischung aus Seminar, Erarbeitung von Forschungsthemen in
Gruppenarbeit sowie aktivem Arbeiten mit Forschungsdaten. Literatur wird abhängig von den
angebotenen Forschungsthemen innerhalb der jeweiligen Veranstaltungen angegeben
werden.
Die Teile können auch in verschiedenen Semestern besucht werden, zum Beispiel Teil 1 im
zweiten Mastersemester und Teil 2 in der Kompaktphase des dritten Mastersemesters nach dem
Praxissemester.
Hinweis: M.Ed.-Studierende, die eine fachdidaktische Masterarbeit in Mathematik
schreiben möchten, müssen das dreiteilige Modul Fachdidaktische Forschung absolvieren.
Interessierte an einer fachdidaktischen Masterarbeit in Mathematik melden sich bitte
zusätzlich bis zum Ende der Vorlesungszeit des aktuellen Semesters in der Abteilung für
Didaktik.
________________________________________________________________________________________
ECTS-Punkte: | (für alle Teile des Moduls zusammen) 4 Punkte |
Verwendbarkeit: | Modul Fachdidaktische Forschung im M.Ed. |
Nützliche Vorkenntnisse: | Grundvorlesungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Prakt. Übung zu: | Numerik (2. Teil der zweisemestrigen Veranstaltung) |
| | |
Dozent: | Prof. Dr. Patrick Dondl |
| | |
Zeit/Ort: | CIP-Pool 201, Hermann-Herder-Str. 10, 2-std. (14-täglich)
n.V. |
| | |
Tutorium: | N.N. |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agdo/lehre/ss21/num2/ |
| | |
| |
_______________________________________________________________
Inhalt:
In der praktischen Übung zur Numerik-Vorlesung sollen die in der Vorlesung entwickelten und
analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird mit Hilfe der
kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme
geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.
Literatur:
-
1.)
- S. Bartels: Numerik 3x9, Springer, 2016.
___________________________________________________________________
ECTS-Punkte: | (für Teil 1 und 2 zusammen) 3 Punkte |
Notwendige Vorkenntnisse: | Vorlesung Numerik (parallel) |
Nützliche Vorkenntnisse: | Einführung in die Programmierung für Studierende der
Naturwissenschaften |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Prakt. Übung zu: | Numerik für Differenzialgleichungen |
| | |
Dozent: | Prof. Dr. Sören Bartels |
| | |
Zeit/Ort: | Do, 10–12 Uhr, voraussichtlich digitales Format (14-tägl.) |
| | |
Tutorium: | M.Sc. Jakob Keck |
| | |
Web-Seite: | http://aam.uni-freiburg.de/agba/lehre/ss21/ndgln |
| | |
| |
_______________________________________________________________
Inhalt:
In der praktischen Übung zur Vorlesung über die Numerik für Differenzialgleichungen sollen die
in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet
werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software
Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare
Programmierkenntnisse werden vorausgesetzt.
Literatur:
-
1.)
- S. Bartels: Numerik 3x9. Springer, 2016
_____________________________________________________________________
ECTS-Punkte: | 1 (mit Vorlesung und Projektarbeit 6 bzw. 9) Punkte |
Verwendbarkeit: | Angewandte Mathematik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
Prakt. Übung zu: | Stochastik (2-Hf.-B.) |
| | |
Dozent: | Prof. Dr. Peter Pfaffelhuber |
| | |
Zeit/Ort: | asynchrones, digitales Angebot |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | Dr. Ernst August v. Hammerstein |
| | |
Anmeldung: | Bitte belegen Sie die Praktische Übung frühzeitig in HISinOne, da-
mit Sie per Mail über den genauen Ablauf und organisatorische
Details informiert werden können! |
| | |
Web-Seite: | https://ilias.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
Erstmalig werden im Sommersemester 2021 die Praktischen Übungen zur Stochastik in zwei
Parallelen angeboten. Die auf dieser Seite beschriebene Parallele ist ausschließlich Hörern der
Vorlesung Stochastik (2-Hf.-B.) vorbehalten, da eine enge inhaltliche Verzahnung mit dieser
Vorlesung angestrebt wird.
Es werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der Vorlesung
vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird das frei verfügbare
Open-Source-Statistikprogramm R verwendet werden. Nach einer Einführung in R werden u.a.
Verfahren der deskriptiven Statistik und graphischen Auswertung von Daten betrachtet, sowie
die in der Vorlesung besprochnene parametrischen Tests diskutiert. Kenntnisse in R und/oder
Programmierkenntnisse werden dabei nicht vorausgesetzt, jedoch im Laufe der Veranstaltung
erworben. Die Anrechenbarkeit beider Parallelen der Praktischen Übung Stochastik ist
identisch.
Für das Nacharbeiten der Lektionen und zur Lösung der darin enthaltenen Übungen sollten alle
Teilnehmenden die dazu benötigte Software (R und RStudio) auf ihren eigenen Rechnern
installieren. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern
möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher
zu R empfohlen werden.______________________________________________________________________________________
ECTS-Punkte: | 3 Punkte |
Verwendbarkeit: | siehe Text |
Notwendige Vorkenntnisse: | Erster Teil der Stochastik-Vorlesung, Analysis 1 |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
Prakt. Übung zu: | Stochastik (B.Sc.) |
| | |
Dozent: | Dr. Ernst August v. Hammerstein |
| | |
Zeit/Ort: | Online-Kurs, Di 10–12 Uhr als Videokonferenz über
BigBlueButton (mit paralleler Aufzeichnung) |
| | |
Übungen: | 2-std. n.V. |
| | |
Tutorium: | Dr. Ernst August v. Hammerstein |
| | |
Anmeldung: | Bitte belegen Sie die Praktische Übung frühzeitig in HISinOne, da-
mit Sie per Mail über den genauen Ablauf und organisatorische
Details informiert werden können! |
| | |
Web-Seite: | https://www.stochastik.uni-freiburg.de/lehre/ss-2021/prakueb-stochastik-ss-2021 |
| | |
| |
_______________________________________________________________
Inhalt:
Dies ist die Parallele der praktischen Übung Stochastik für B.Sc.-Studierende, die sich
an die entsprechenden Hörerinnen und Hörer der Vorlesung Stochastik richtet. Es
werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der
Vorlesung vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird
das frei verfügbare Open-Source-Statistikprogramm R verwendet werden. Nach einer
Einführung in R werden u.a. Verfahren der deskriptiven Statistik und graphischen
Auswertung von Daten betrachtet, die numerische Erzeugung von Zufallszahlen erläutert
sowie parametrische und nichtparametrische Tests und lineare Regressionsverfahren
diskutiert. Vorkenntnisse in R und/oder Programmierkenntnisse werden dabei nicht
vorausgesetzt.
Die praktische Übung ist für Studierende im (1-Hauptfach) B.Sc. Mathematik obligatorisch. Im
Studiengang Master of Education kann die Veranstaltung als Mathematische Ergänzung belegt
werden. Sie soll als Videokonferenz über BigBlueButton zu einem festen wöchentlichen Termin
stattfinden, um allen Teilnehmenden die Möglichkeit zu geben, Fragen zu stellen und diese direkt
beantwortet zu bekommen. Sofern alle jeweils dazu eingeloggten Studierenden einverstanden
sind, können die Sitzungen parallel aufgezeichnet und die Videos allen über die Lernplattform
ILIAS zur Verfügung gestellt werden.
Für das Nacharbeiten der Lektionen und zur Lösung der darin enthaltenen Übungen sollten
alle Teilnehmenden die dazu benötigte Software (R und RStudio) auf ihren eigenen
Rechnern installieren. Genauere Anleitungen hierzu sowie Links zum Download der
kostenlosen Programme werden frühzeitig auf der o.g. Webseite bekannt gegeben
werden.
Zu den einzelnen Lektionen der praktischen Übung wird ein ausführliches Skriptum bereitgestellt
werden. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern
möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher
zu R empfohlen werden.______________________________________________________________________________________
ECTS-Punkte: | 3 Punkte |
Verwendbarkeit: | Pflichtveranstaltung im B.Sc. Mathematik
M.Ed.: Möglich als Mathematische Ergänzung (sofern nicht
schon im 2-Hf-Bachelor-Studiengang belegt) |
Notwendige Vorkenntnisse: | Analysis I und II, Lineare Algebra I und II, Stochastik (1. Teil) |
| |
3. Seminare
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
In dem Proseminar werden ausgewählte schöne Resultate aus der Analysis mit elementaren
Methoden bewiesen.
Literatur:
-
1.)
- Naas, Tutschke: Große Sätze und schöne Beweise der Mathematik, Verlag Harry Deutsch
(1997)
-
2.)
- Aigner, Ziegler: Das Buch der Beweise, Springer (2015)
________________________________________________
Notwendige Vorkenntnisse: | Analysis I, II |
Nützliche Vorkenntnisse: | variiert je nach Vortrag |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Dieses Proseminar richtet sich insbesondere auch an
Studierende des 2-Hf BSc Mathematik |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
Proseminar: | Diskrete Finanzmathematik |
| | |
Dozent: | Dr. Ernst August v. Hammerstein |
| | |
Zeit/Ort: | Di 16–18
Uhr, HS II, Albertstr. 23b (falls als Präsenzveranstaltung
möglich) oder zeitgleich als BBB-Videokonferenz |
| | |
Tutorium: | Dr. Ernst August v. Hammerstein |
| | |
Voranmeldung: | Interessenten melden bitte ihren Teilnahmewunsch bis spätestens
zum 06.02.2021 per Mail an
|
| | |
Vorbesprechung: | Di, 09.02.2021, um 14:30 Uhr per Videokonferenz im virtuellen
BigBlueButton-Sprechstundenraum vHammerstein |
| | |
Web-Seite: | https://www.stochastik.uni-freiburg.de/lehre/ss-2021/proseminar-finanzmathematik-ss-2021 |
| | |
| |
_______________________________________________________________
Inhalt:
Seit der Veröffentlichung der Black-Scholes-Formel zur Optionspreisbewertung im Jahr 1973 hat
die moderne Finanzmathematik eine stürmische Entwicklung genommen. Parallel zur
Entwicklung immer neuer Derivate wurden und werden auch zunehmend komplexere
stochastische Modelle entwickelt, um erstere zu bewerten und deren Risiken adäquat
abschätzen zu können. Die Beschäftigung mit diesen Modellen setzt jedoch vertiefte
Kenntnisse in zeitstetigen stochastischen Prozessen und stochastischer Analysis voraus, wie
sie üblicherweise erst in Master-Studiengang mit Schwerpunkt Stochastik erworben
werden.
Die Grundideen und -Prinzipien, auf denen die komplexen Modelle beruhen (und die sie
weiterentwickeln), lassen sich jedoch oft schon in deutlich einfacherem Rahmen und
diskreter Zeit darstellen und verstehen. Genau das soll Thema dieses Proseminars sein.
Anhand der u.g. Bücher sowie evtl. einzelner weiterer Quellen wollen wir uns in die
diskrete Finanzmathematik einarbeiten, einige von deren zentralen Methoden und
Begriffen kennenlernen sowie die Bewertung von Derivaten und Risikomanagement
diskutieren.
Literatur:
-
1.)
- M.U. Dothan: Prices in Financial Markets, (Kap. 1–6), Oxford University Press, 1990.
-
2.)
- A. Irle: Finanzmathematik, (3. Auflage, Kap. 1–5), Springer Spektrum, 2012.
Als elektronischer Volltext (innerhalb des Uni-Netzes) verfügbar unter
https://link.springer.com/book/10.1007%2F978-3-8348-8314-8
-
3.)
- J. Kremer: Portfoliotheorie, Risikomanagement und die Bewertung von Derivaten
(2. Auflage), Springer, 2011. Als elektronischer Volltext (innerhalb des Uni-Netzes) verfügbar
unter
https://link.springer.com/book/10.1007%2F978-3-642-20868-3
__________________
Notwendige Vorkenntnisse: | Grundvorlesungen Analysis, Lineare Algebra und Stochastik
(1. Teil) |
Bemerkung: | Das Proseminar ist auch für Studierende des
2-Hf-Bachelor-Studienganges geeignet. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Graphen sind ganz einfache geometrische Gebilde, die nur aus Kanten und Ecken bestehen. Sie
kommen an vielen verschiedenen Stellen in der Mathematik, aber auch im wirklichen Leben z.B.
als Stadpläne oder Telefonleitungen vor. Beliebt sind sie auch in mathematischen Rätseln wie
dem Haus vom Nikolaus.
Wir wollen einige ihrer sehr vielfältigen Eigenschaften kennenlernen und studieren.
Literatur:
-
1.)
- R. Diestel. Graph Theory. Fourth edition. Graduate Texts in Mathematics, 173. Springer,
Heidelberg, 2010
-
2.)
- D. West. Introduction to Graph Theory. Prentice Hall, Inc., Upper Saddle River, NJ, 1996.
-
3.)
- B. Bollobás. Modern Graph Theory. Graduate Texts in Mathematics, 184. Springer-Verlag,
New York, 1998
____________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Lineare Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Im täglichen Leben hilft die Mathematik, Probleme aus verschiedensten Bereichen zu
beschreiben, zu verstehen und zu lösen. Das beginnt bei Fragen wie der Taschenrechner den
Sinus eines Winkels berechnet und ist die Basis für viele moderne technische Errungenschaften
des modernen Lebens von Datenverarbeitung, Kommunikation und Lokalisationsaufgaben. In
den Vorträgen soll es darum gehen, einzelne Anwendungen zunächst vorzustellen, das
zugrundeliegende mathematische Problem herauszuarbeiten und dann seine Lösung zu
präsentieren.
Eigene Themenvorschäge der Teilnehmerinnen und Teilnehmer sind willkommen, sofern sie in
den Rahmen des Proseminars passen. In diesem Fall bitten wir, rechtzeitig vor der
Vorbesprechung mit uns Kontakt aufzunehmen.
Eine Liste möglicher Themen wird sich bis Ende Januar auf der obigen Webseite finden._
Notwendige Vorkenntnisse: | Grundvorlesungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Lehramtsstudierende haben Vorrang |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Das Seminar zur Kommutativen Algebra und Algebraischen Geometrie ergänzt die
Vorlesung „Kommutative Algebra und Einführung in die Algebraische Geometrie“, die
parallel angeboten wird, kann aber unabhängig von der Vorlesung belegt werden.
Ziel ist es, die enge Verbindung von Algebra und Geometrie zu beleuchten, und die
abstrakten Begriffsbildungen der kommutativen Algebra durch geometrische Beispiele zu
erläutern.
Literatur:
-
1.)
- Andreas Gathmann: Algebraic Geometry, http://www.mathematik.uni-kl.de/agag/mit
glieder/professoren/gathmann/notes/alggeom
-
2.)
- Igor Dolgachev : Introduction to Algebraic Geometry,
http://www.math.lsa.umich.edu/~idolga/lecturenotes.html
______________________
Notwendige Vorkenntnisse: | Vorlesung: Lineare Algebra I und II |
Nützliche Vorkenntnisse: | Vorlesung: Algebra und Zahlentheorie |
Folgeveranstaltungen: | Wir planen, im WS 2021/22 weiterführende Veranstaltungen
zur Algebraischen Geometrie anzubieten |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Wir behandeln die Integration von Differentialformen auf abstrakten, differenzierbaren
Mannigfaltigkeiten. Diese werden ebenfalls im Seminar eingeführt. Ein Resultat ist der Satz von
Stokes, eine Version des Satzes von Gauß. Im Anschluss definieren wir als Anwendung eine
topologische Invariante, den Abbildungsgrad. Dieser ist zur Lösung nichtlinearer Gleichungen
ein wesentliches Hilfsmittel. Je nach Zeit können wir das Konzept auch auf gewisse
Abbildungen zwischen Banachräumen verallgemeinern, und auf die Lösbarkeit partieller
Differentialgleichungen anwenden. Die Gewichtung der Teile richtet sich auch nach den
Vorkenntnissen der Teilnehmer/innen.
Literatur:
-
1.)
- J. Lee, Introduction to smooth manifolds, Springer Graduate Texts in Mathematics, Springer
2012.
-
2.)
- L. Nirenberg, Topics in nonlinear functional analysis, Lecture Notes, Courant Institute New
York 1973.
___________________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Analysis III, Lineare Algebra II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Seminar: | Geometrische Variationsrechnung |
| | |
Dozent: | Prof. Dr. Guofang Wang |
| | |
Zeit/Ort: | Mi 16–18 Uhr, HS II, Albertstr. 23b |
| | |
Tutorium: | N.N. |
| | |
Vorbesprechung: | Mi, 10.2. 2021, 15 Uhr, BBB-Raum vWang |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/wang/ |
| | |
| |
_______________________________________________________________
Inhalt:
Variationsrechnung ist eines der ältesten Teilgebiete der Analysis. In der Variationsrechnung geht
es darum, Extremstellungen von Funktionalen zu finden. Viele Fragestelle aus der Geometrie
(Geodätischen, d.h. kürzeste Verbindung zwischen zwei Punkten; Minimalflächen), der partiellen
Differentialgleichungen, und der Physik (klassischen Mechanik, Optik und Feldtheorie) führen
auf unendlichendimensionale Extremwertaufgaben. In dem Seminar werden die direkte Methode,
sowie die Minimax-Methode untersucht.
Literatur:
-
1.)
- Struwe, Variational Methods. Third edition. Ergebnisse der Mathematik und ihrer
Grenzgebiete, 4. Folge, A Series of Modern Surveys in Mathematics, 34, Springer-Verlag,
Berlin, 2008
________________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Funktionalanalysis oder Einführung in PDE oder PDE I |
Nützliche Vorkenntnisse: | Variationsrechnung |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Bachelor- oder Masterarbeit |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Moduli spaces parametrising objects associated with a given variety X are a rich source of
spaces with interesting structures. Not only do they inherit various properties from X, but they
may also bring to light hidden structures that cannot be accessed via the original
variety.
The purpose of this seminar is to explore an example of this phenomenon. We shall introduce the
Hilbert scheme X[n] of a smooth surface X parametrising n-tuples of points of X. We shall study
its geometric properties and establish, among other things, the non-trivial fact that X[n] is itself
a smooth variety. One of the new and surprising features of X[n] is that one can construct a
representation of the so-called Heisenberg algebra on its cohomology groups. We shall see that
this is not just a pretty result, but it is also very useful in understanding how characteristic
classes of line bundles on X relate to those of certain interesting vector bundles on X[n].
Moreover, this construction also provides a connection to mathematical physics as it
gives a geometric realisation of a formula for the Euler characteristic of the moduli
space of N = 4 Yang-Mills instantons, though this will be beyond the scope of our
seminar.
Literatur:
-
1.)
- M. Lehn, Chern classes of tautological sheaves on Hilbert schemes of points on surfaces,
Inventiones Mathematicae 136 (1999) 157–207
-
2.)
- E. Miller, B. Sturmfels, Combinatorial Commutative Algebra, Springer 2005
-
3.)
- H. Nakajima, Lectures on Hilbert Schemes of Points on Surfaces, AMS 1999
_____________________
Notwendige Vorkenntnisse: | Kommutative Algebra Vorlesung, Grundkentnisse in
Komplexer Geometrie |
Nützliche Vorkenntnisse: | Lie Algebren, Garben, Schemata |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Mathematische Logik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Wir betrachten Boreläquivalenzrelationen E auf einem separablen vollständig metrisierten
Raum X, d.h. E ist eine Borelteilmenge von X × X. Eine bemerkenswert komplizierte
Äquivalenzrelation ist die Vitalirelation E0 ⊆ 2ℕ × 2ℕ, die für x,y ∈ 2ℕ sagt
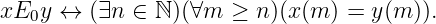
Harrington, Kechris und Louveau bewiesen 1990 einen bahnbrechenden Dichotomiesatz, der
anschaulich gesprochen sagt: Für jede Boreläquivalenzrelation gibt es entweder eine
Borelfunktion, die den Klassen Invarianten zuordnet, oder die Äquivalenzrelation ist mindestens
so kompliziert wie die Vitalirelation. Letztere hat natürlich keine Borelinvarianten.
Die aus der linearen Algebra bekannte Äquivalenz von ℂn×n-Matrizen ist eine Relation des ersten
Typs, wie die Jordan’sche Normalform zeigt. Die Alternative zwei für E ist äquivalent zur
Existenz eines E-ergodischen atomlosen Maßes auf X.
Im Seminar studieren wir die Arbeit von Harrington, Kechris und Louveau, die einen recht
geschlossenen Beweis liefert. Dieser baut auf der Theorie der Choquet-Spiele und der effektiven
deskriptiven Mengenlehre auf und benutzt etliche eigens entwickelte kombinatorische Kniffe. Das
Thema ist für Abschlussarbeiten geeignet.
Literatur:
-
1.)
- E.G. Effros Transformation Groups and C* Algebras, Ann. of Math. 81 (1965), 38–55.
-
2.)
- J. Glimm. Type I C* Algebras, Ann. of Math. 73 (1961), 572–612.
-
3.)
- L. Harrington, A. Kechris, A. Louveau A Glimm-Effros Dichotomy for Borel Equivalence
Relations, Journal of the Amer. Math. Soc. 3(4) (1990), 903–928.
_________________________________________________________________________________________________________________________
Nützliche Vorkenntnisse: | Maßtheorie, Mathematische Logik, etwas Topologie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Seminar: | Mathematische Bildverarbeitung |
| | |
Dozent: | Prof. Dr. S. Bartels |
| | |
Zeit/Ort: | Mo, 14–16 Uhr, SR 226 (HH 10), ggf. als Online-Seminar |
| | |
Tutorium: | M.Sc. Ludwig Striet, N.N. |
| | |
Vorbesprechung: | Mi, 10.2.2021, ab 13:15 Uhr, per Videokonferenz |
| | |
Teilnehmerliste: | Anmeldung bis zum 8.2.2021 per E-Mail an Frau Tress
elvira.tress@mathematik.uni-freiburg.de |
| | |
| |
_______________________________________________________________
Inhalt:
Im Seminar soll die Anwendung von Techniken der Theorie und Numerik partieller
Differentialgleichungen auf Fragestellungen der mathematischen Bildverarbeitung diskutiert
werden. Dazu gehören die Themen:
- Industrielle Anwendungen, Bildmodelle
- Nichtlineare Filter und quasilineare partielle Differentialgleichungen
- Numerische Lösung von Allen–Cahn- und p-Laplace-Gleichungen
- Funktionen beschränkter Variation und das ROF-Modell
- Numerische Behandlung des ROF-Modells
- Fraktionelle Modelle und Lösung mittels FFT
- Harmonische Abbildungen und Farbbildbehandlung
- Bildsegmentierung und das Mumford-Shah-Modell
- Störungsmodelle und Maße zur Qualitätsbeurteilung
- Bilderkennung und maschinelles Lernen
- Wavelet-Transformation und Bildkompression
- Shannon’sches Abtasttheorem und Anwendungen
Die Themen sind voneinander unabhängig. Bei Anmeldung zum Seminar können zwei
Wunschthemen angegeben werden, darüberhinaus erfolgt die Vergabe zufällig.
Literatur:
-
1.)
- G. Aubert, P. Kornprobst: Mathematical Problems in Image Processing. Springer, 2006.
-
2.)
- S. Bartels: Numerical Methods for Nonlinear PDEs. Springer, 2015.
-
3.)
- K. Bredies, D. Lorentz: Mathematische Bildverarbeitung. Springer-Vieweg, 2011.
-
4.)
- C. Demant, B. Streicher-Abel, A. Springhoff: Industrielle Bildverarbeitung. Springer, 2011.
-
5.)
- B. Neumann: Bildverarbeitung für Einsteiger. Springer, 2005.
____________________________________________________________________________________
Notwendige Vorkenntnisse: | Vorlesung Einführung in Theorie und Numerik partieller Dgl’n
oder Partielle Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Angewandte Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Seminar: | Verallgemeinerte Newtonsche Fluide |
| | |
Dozent: | Prof. Dr. M. Růžička |
| | |
Zeit/Ort: | Fr 10–12 Uhr, SR 127, Ernst-Zermelo-Str. 1, BBB-Raum
vRuzicka |
| | |
Tutorium: | A. Kaltenbach |
| | |
Vorbesprechung: | Do, 4.02.2021, ab 11 Uhr, online in vRuzicka |
| | |
Teilnehmerliste: | Bei Interesse melden Sie sich bitte bis zum 2.2.2021 per E-Mail bei
Frau Tress elvira.tress@mathematik.uni-freiburg.de |
| | |
| |
_______________________________________________________________
Inhalt:
Im Seminar werden moderne Techniken diskutiert, die die Theorie pseudomonotoner
Operatoren, welche in der Vorlesung „Nichtlineare Funktionalanalysis“ behandelt
wurde, erweitern. Diese Techniken werden auf die Existenztheorie verallgemeinerter
Newtonscher Fluide angewendet. Die behandelten Themen eignen sich als Grundlage für
Masterarbeiten._________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Nichtlineare Funktionalanalysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Imbalanced data sets are known to significantly reduce the performance of classifiers in
statistical learning: Learning algorithms designed for equally balanced classes tend to be biased
towards the majority class. This is a problem because typically, the minority class is more
important and therefore the problem is more sensitive to classification errors for the minority
class than the majority class. Besides efforts to improve the data mining process,
strategies to overcome this deficiency are either synthetic oversampling, where synthetic
minority class examples are generated, or subsampling from the majority class to
reduce the number of majority class examples. The latter has the appealing property of
reducing the computational complexity – however, it may result in a loss of efficiency,
as valuable information is unregarded. Yet, there is no general guidance on when to
use each technique. In this seminar, we shall gain some insight on this important
problem, studying a combination of rather theoretical and more applied statistical
literature.
Literatur:
-
1.)
- Wird in derVorbesprechung bekanntgegeben.
_________________________________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Stochastik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
In diesem Seminar werden wir aktuelle Arbeiten im Bereich stochastisches Maschinelles Lernen
behandeln. Dazu gibt es sowohl theoretische als auch praktische Arbeiten.
Vorkenntnisse in Stochastik und Finanzmathematik sind hilfreich, aber nicht unbedingt
nötig.
Literatur:
-
1.)
- Wird in der Vorbesprechung bekanntgegeben.
_________________________________________________________________________________________________________________________
Nützliche Vorkenntnisse: | Stochastik und Finanzmathematik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Institut für
Medizinische Biometrie und
Statistik
SS2021
__________________________________________________________________________________________________________________________________________________________
_______________________________________________________________
Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft
ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder
allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data
Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als
Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt
werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue
thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein
oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik
dienen.
Vorbesprechung mit Hinweisen auf einführende Literatur:
Mittwoch den 10.2.2021, 10:30–11:30 Uhr (online, Zugangsdaten werden verschickt).
Vorherige Anmeldung per E-Mail (sec@imbi.uni-freiburg.de) ist dafür notwendig._____
Notwendige Vorkenntnisse: | gute Kenntnis in Wahrscheinlichkeitstheorie und
Mathematischer Statistik |
Folgeveranstaltungen: | kann als Vorbereitung für eine Masterarbeit dienen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
|
| |
4. Projektseminare, Lesekurse
und Kolloquien
Mathematisches Institut
SS2021
__________________________________________________________________________________________________________________________________________________________
Lesekurs: | Wissenschaftliches Arbeiten |
| | |
Dozent: | Alle Professor/inn/en und Privatdozent/inn/en des
Mathematischen Instituts |
| | |
Zeit/Ort: | nach Vereinbarung |
| | |
| |
_______________________________________________________________
Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen
Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen
einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im
Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit
einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der
Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der
Lesekurs im Idealfall als Vorbereitung auf die Master-Arbeit dient (im M.Sc. wie im
M.Ed.).
Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen
(typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums,
eventuell Vorträge in einer Arbeitsgruppe, einem Oberseminar, Projektseminar …) werden zu
Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung
sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.
Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung
bestanden ist oder nicht. Im M.Ed. und im Modul „Mathematik“ des M.Sc. gibt es eine
mündliche Abschlussprüfung über den Stoff des Lesekurses, im Vertiefungsmodul des M.Sc. eine
mündliche Abschlussprüfung über sämtliche Teile des Moduls. Ein Lesekurs zur Vorbereitung auf
die Master-Arbeit kann im M.Sc. auch im Wahlmodul angerechnet werden (ohne Prüfung, nur
Studieneistung).
Im M.Sc.-Studiengang ist daran gedacht, dass Sie einen, maximal zwei Lesekurse absolvieren.
Verwendbarkeit: | M.Ed.: Modul Wissenschaftliches Arbeiten
M.Sc.: Vertiefungsmodul, Wahlmodul, Modul Mathematik |
Notwendige Vorkenntnisse: | hängen vom einzelnen Lesekurs ab |
| |
Abteilung für
Reine Mathematik
SS2021
__________________________________________________________________________________________________________________________________________________________
Projektseminar: | Seminar des Graduiertenkollegs GK 1821 |
| | |
Dozent: | Die Dozentinnen und Dozenten des Graduiertenkollegs |
| | |
Zeit/Ort: | Mi 14–16 Uhr, Onlinepräsenz |
| | |
Web-Seite: | https://www.gk1821.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Content:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in
Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology
or mathematical physics or a mix thereof.
The precise topic will be chosen at the end of the preceeding semester. The program will be
made available via our web site.
The level is aimed at our doctoral students. Master students are very welcome to participate as
well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. Annette
Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________
ECTS-Punkte: | im M.Sc.-Studiengang 6 Punkte |
Notwendige Vorkenntnisse: | je nach Thema, meist algebraische Geometrie |
| |
SS2021
__________________________________________________________________________________________________________________________________________________________
Veranstaltung: | Kolloquium der Mathematik |
| | |
Dozent: | Alle Dozentinnen und Dozenten der Mathematik |
| | |
Zeit/Ort: | Do 17:00 Uhr, Hörsaal II, Albertstr. 23b |
| | |
| |
_______________________________________________________________
Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des
gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet
sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.
Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag
um 17:00 Uhr im Hörsaal II in der Albertstraße 23b statt.
Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Ernst-Zermelo-Straße 1 den
wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.
Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/