Lehrveranstaltungen

Inhalt:
In der Vorlesung soll eine Einführung in die Elementargeometrie im euklidischen und nicht-euklidischen Raum und seine mathematischen Grundlagen gegeben werden. Wir behandeln im Einzelnen dazu die Themen der Axiomatik, Isometrien-Bewegungsgruppe und Trigonometrie der euklidischen, hyperbolischen und sphärischen Geometrie. Im weiteren Verlauf schauen wir uns die Geschichte des fünften Euklidischen Axioms (und die Versuche, es los zu werden) an, diskutieren die kontraintuitiven Ergebnisse der daraus hervorgegangen hyperbolischen Geometrie (z.B. existieren dort Dreiecke mit der Innenwinkelsumme Null). Ferner geben wir eine Einführung in die Projektive Geometrie und betrachten Polygone, Polyeder und deren Eigenschaften.

Literatur:

1.)

C. Bär: Elementare Differentialgeometrie (2. Auflage), De Gruyter, 2010.

2.)

M. Berger: Geometry I (Corrected Third Printing), Springer Universitext, 2004.

3.)

R. Hartshorne: Geometry: Euclid and beyond, Springer, 2000.

4.)

H. Knörrer: Geometrie (2. Auflage), Springer Vieweg, 2006.

Inhalt:
Die Funktionalanalysis ist ein wichtiges Hilfsmittel für viele zentrale Resultate in der Mathematik. Funktionale sind lineare Abbildungen, und das besondere bei der Betrachtung in dieser Vorlesung ist, dass diese unendlichdimensional sein werden. Beispiele für solche lineare Abbildungen sind Differential- oder Integraloperatoren, wobei ein geeigneter Konvergenzbegriff verwendet wird. Im Gegensatz zur Analysis auf endlichdimensionalen Räumen entstehen ungewohnte Effekte, wie z.B. dass lineare Abbildungen unstetig sein können, Fixpunkteigenschaften verloren gehen können, etc.

In dieser Vorlesung lernen wir die zentralen Resultate kennen wie der Satz von Hahn-Banach, verschiedene Funktionenräume der Funktionalanalysis, der weit reichende Baire’sche Kategoriensatz, schwache Topologien und Spektraltheorie. Ebenfalls werden Anwendung in der Stochastik und in der Finanzmathematik als Beispiele diskutiert.

Literatur:

1.)

H. Brezis: Functional Analysis, Sobolev Spaces and Partial Differential Equations, Springer, 2011.

2.)

D. Werner: Funktionalanalysis (8. Auflage), Springer Spektrum, 2018.

3.)

M. Fabian, P. Habala et al.: Functional Analysis and Infinite-Dimensional Geometry, Springer, 2001.

Content:
Lie theory is a subject lying at the intersection of algebra and geometry: a Lie group is a smooth manifold with a group structure such that the group operations are smooth. Lie groups arise in a natural way as symmetries of geometric objects: prominent examples of Lie groups are the general linear group GL_n(ℝ) or the orthogonal group O_n(ℝ). In addition, also the tangent space of a Lie group is equipped in a natural way with a particular algebraic structure, known as Lie algebra.

In this lecture course, we will introduce the notion of Lie groups and Lie algebras and discuss the correspondence between them. The focus of the course will be on compact Lie groups, an important class of Lie groups for which the theory is very rich and well-developed. We will study and classify representations of compact Lie groups, that is smooth linear actions on vector spaces. As a concrete final goal, we will classify compact Lie groups in terms of more elementary data: root systems.

Literature:

1.)

A.W. Knapp: Lie Groups Beyond an Introduction (Second Edition), Birkhäuser, 2002.

2.)

M. Sepanski: Compact Lie Groups, Springer, 2007.

3.)

W. Soergel: Lecture notes Mannigfaltigkeiten und Liegruppen, available at http://home.mathematik.uni-freiburg.de/soergel/Skripten/XXML.pdf.

Inhalt:
In dieser Vorlesung sollen zunächst Begriffe und Methoden rund um Faserbündel behandelt werden. Diese bilden die grundlegenden Begriffe zur Behandlung vieler geometrischer Probleme auf gekrümmten Räumen sowie zur mathematischen Modellierung von Eichfeldtheorien in der theoretischen Physik. So ist z.B. der Elektromagnetismus ein einfaches Beispiel einer Eichfeldtheorie. Als weiteres Beispiel werden wir als nichtabelsche Eichtheorie die Yang-Mills Theorie behandeln.

Im zweiten Teil der Vorlesung behandeln wir elliptische Differentialoperatoren auf Mannigfaltigkeiten und Bündeln, insbesondere den Laplaceoperator und soweit die Zeit zulässt den Diracoperator.

Literatur:

1.)

H. Baum: Eichfeldtheorie, Springer, 2014.

Inhalt:
Die Funktionentheorie ist ein klassisches Gebiet der höheren Mathematik und befasst sich mit der Differential- und Integralrechnung für komplex differenzierbare Funktionen in einer komplexen Veränderlichen. Diese können natürlich auch als Funktionen zweier reeller Veränderlichen aufgefasst werden und sind dann dadurch charakterisiert, dass sie die sogenannten Cauchy-Riemannschen Differentialgleichungen lösen. Die überraschenden Ergebnisse der Funktionentheorie können auf die besonders schönen Eigenschaften dieser Differentialgleichungen zurückgeführt werden. Zum Beispiel sind komplex differenzierbare Funktionen automatisch nicht nur beliebig oft stetig differenzierbar, sondern immer analytisch, können also lokal als Potenzreihen dargestellt werden. Außerdem ist eine komplex differenzierbare Funktion durch erstaunlich wenig Daten eindeutig bestimmt: Ihre Werte auf einer Kreisscheibe sind schon durch ihre Werte auf dem Rand dieser Kreisscheibe eindeutig festgelegt. Diese Tatsachen machen den Umgang mit komplex differenzierbaren Funktionen besonders einfach. Die vielen schönen Eigenschaften komplex differenzierbarer Funktionen erlauben zahlreiche Anwendungen in verschiedensten Gebieten der Mathematik und Physik.

Zentrale Themen der Vorlesung sind die Grundlagen der Funktionentheorie, also insbesondere Cauchy-Riemannsche Differentialgleichungen, der Cauchysche Integralsatz, die Cauchysche Integralformel, Maximumprinzip und Residuensatz. Sofern die Zeit es erlaubt, werden außerdem Anwendungen in der Zahlentheorie angesprochen, z.B. der Beweis des Primzahltheorems.

Literatur:

1.)

K. Jänich: Funktionentheorie (6. Auflage), Springer, 2004 (korrigierter Nachdruck 2008).

2.)

E. Freitag, R. Busam: Funktionentheorie (4. Auflage), Springer, 2006.

3.)

S. Lang: Complex Analysis (Fourth Edition), Springer, 1999.

4.)

R. Remmert, G. Schumacher: Funktionentheorie I (5. Auflage), Springer, 2002.

Content:
Four decades ago David Mumford wrote that algebraic geometry “seems to have acquired the reputation of being esoteric, exclusive, and very abstract, with adherents who are secretly plotting to take over all the rest of mathematics! ...”

The purpose of this course is to introduce students with some commutative algebra background to modern algebraic geometry via the theory of algebraic curves and without excessive prerequisites. Algebraic curves are the algebraic counterparts of Riemann surfaces and constitute a very rich topic with connections to number theory, representation theory, complex analysis, and mathematical physics.

Special emphasis will be placed on examples and on developing intuition for how the abstract language of commutative algebra can be used to express geometric ideas. Topics covered include: linear series on curves, intersection theory, and the Riemann–Roch problem.

Literature:

1.)

W. Fulton: Algebraic Curves—An Introduction to Algebraic Geometry (Reprint of 1969 original), Addison-Wesley, 1989.

Inhalt:
Es wird eine Einführung in die klassische Differentialgeometrie im Euklidischen Raum gegeben. Im Vordergrund steht dabei die Frage, was die Krümmung einer Kurve bzw. Fläche ist und welche geometrische Bedeutung sie für die Kurve bzw. Fläche als Ganzes hat. Entlang der Theorie werden zahlreiche Beispiele behandelt.

Literatur:

1.)

C. Bär: Elementare Differentialgeometrie (2. Auflage), de Gruyter, 2010.

2.)

M.P. do Carmo: Differential Geometry of Curves and Surfaces (Second Edition), Dover, 2016.

3.)

J.-H. Eschenburg, J. Jost: Differentialgeometrie und Minimalflächen (3. Auflage), Springer, 2014.

Content:
The aim of the course is to give an introduction into numerical methods for the solution of optimal control problems in science and engineering. The focus is on both discrete time and continuous time optimal control in continuous state spaces. It is intended for a mixed audience of students from mathematics, engineering and computer science.

The course covers the following topics: Introduction to Dynamic Systems and Optimization

• Rehearsal of Numerical Optimization
• Rehearsal of Parameter Estimation
• Discrete Time Optimal Control
• Dynamic Programming
• Continuous Time Optimal Control
• Numerical Simulation Methods
• Hamilton–Jacobi–Bellmann Equation
• Pontryagin and the Indirect Approach
• Direct Optimal Control
• Differential Algebraic Equations
• Periodic Optimal Control
• Real-Time Optimization for Model Predictive Control.

The lecture is accompanied by intensive weekly computer exercises based on MATLAB (6 ECTS) and an optional project (3 ECTS). The project consists in the formulation and implementation of a self-chosen optimal control problem and numerical solution method, resulting in documented computer code, a project report, and a public presentation.

Literature:

1.)

Manuscript Numerical Optimal Control by M. Diehl and S. Gros.

2.)

L.T. Biegler: Nonlinear Programming, SIAM, 2010.

3.)

J. Betts: Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, SIAM, 2010.

Inhalt:
Die algebraische Topologie untersucht topologische Räume mit algebraischen Methoden. Typische Fragen sind

• Gibt es (topologische) Räume mit den Eigenschaften …?
• Gibt es (stetige) Abbildungen von X nach Y mit den Eigenschaften …?
• Sind zwei gegebene Räume oder Abbildungen in einem gewissen Sinne „gleich“?

Methoden der algebraischen Topologie werden in vielen Bereichen der Mathematik, insbesondere in der Geometrie eingesetzt.

In diesem Teil der Vorlesung führen wir Kohomologie axiomatisch ein, inklusive Cup- und Cap-Produkten, Orientierungen, und lernen wichtige Resultate wie den Thom-Isomorphismus sowie Spanier-Whitehead- und Poincaré-Dualität kennen.

Multiplikative Kohomologietheorien lassen sich durch Ringspektren darstellen. Wir behandeln neben klassischer Kohomologie auch K-Theorie und Kobordismus. Spektren erlauben auch einen klareren Blick auf Kohomologie-Operationen und Abbildungen zwischen verschiedenen Kohomologietheorien, wie zum Beispiel charakteristische Klassen.

Literatur:

1.)

T. tom Dieck: Topologie, de Gruyter, Berlin-New York, 1991.

2.)

T. tom Dieck: Algebraic Topology, EMS Textbooks in Mathematics, EMS, 2008.

3.)

A. Hatcher: Algebraic Topology, Cambridge University Press, 2002, http://www.math.cornell.edu/~hatcher/AT/ATpage.html.

4.)

R.M. Switzer: Algebraic topology—homotopy and homology, Grundlehren, Band 212, Springer, 1975.

Inhalt:
Die Veranstaltung schließt an die Vorlesungen Stochasische Prozesse aus dem WS2019 an. Ein zentrales Thema sind stochastische Integrale der Form ∫ H_sdW_s, wobei (H_t)_t≥0 ein adaptierter Prozess und (W_t)_t≥0 eine Brownsche Bewegung ist. Darauf aufbauend werden die Itô-Formel und stochastische Differentialgleichungen behandelt. Ebenso werden wir einige Anwendungen der vorgestellten Theorie besprechen.

Literatur:

1.)

A. Klenke: Wahrscheinlichkeitstheorie (3. Auflage), Springer, 2013.

2.)

O. Kallenberg: Foundations of Modern Probability (Second Edition), Springer, 2002.

3.)

P. Protter: Stochastic Integration and Differential Equations (Second Edition, Version 2.1), Springer, 2005.

Inhalt:
In der Algebraischen Zahlentheorie lösen wir Gleichungen, wobei wir allerdings nur an ganzzahligen Lösungen interessiert sind. Also z.B. für festes n die Frage, für welche Zahlen x,y,z ∈ ℤ die Gleichung

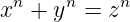
gelöst wird. Viele klassische Fragen aus der Zahlentheorie lassen sich in solche Probleme umformulieren. Beispielsweise kann man fragen, wie viele aufeinanderfolgende ganze Zahlen es gibt, die echte Potenzen sind (also mⁿ mit n ≥ 2). Dies ist äquivalent zu der Frage, welche positiven ganzzahligen Lösungen die Gleichung

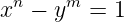
besitzt. Hier hatte Catalan 1844 vermutet, dass dies nur 8 = 2³ und 9 = 3² sind. Euler hatte zuvor bereits den Spezialfall x² - y³ = 1 behandeln können, aber ein vollständiger Beweis der Catalanschen Vermutung ist erst im Jahr 2002 gelungen (Satz von Mihailescu) und nutzt ganz zentral die Algebraische Zahlentheorie.

In der Analysis nutzt man oft Methoden, die schrittweise eine Lösung annähern (man denke z.B. an den Fixpunktsatz von Banach oder die numerische Suche nach Nullstellen von Polynomen). Aber diese Methoden helfen hier nicht, denn es ist zunächst unmöglich zu kontrollieren, ob der Grenzwert einer so entstehenden Folge eine Ganzzahl ist oder nicht. Stattdessen nutzt man in der algebraischen Zahlentheorie eher Teilbarkeitsmethoden: Primzahlen und gewisse Verallgemeinerungen (Primideale) rücken in den Mittelpunkt.

Literatur:

1.)

J. Neukirch: Algebraische Zahlentheorie, Springer, 1992.

2.)

S. Lang: Algebraic Number Theory (2. Auflage), Springer, 1994.

3.)

J. Milne: Algebraic Number Theory, Online lecture notes, verfügbar unter https://www.jmilne.org/math/CourseNotes/ANT.pdf.

4.)

F. Lorenz: Algebraische Zahlentheorie, BI-Wissenschaftsverlag, 1993.

Inhalt:
Dies ist eine Einführung in die mathematische Logik. Wir werden den Begriff eines mathematischen Beweises präzisieren. Für den festgelegten Beweisbegriff beantworten wir dann folgende Fragen: Von welchen (nicht beweisbaren) Grundprinzipien geht man aus? Kann man das Nachprüfen oder gar das Finden von Beweisen geeigneten Computern überlassen? Gegenstände der Vorlesung sind der Gödelsche Vollständigkeitssatz und die Gödelschen Unvollständigkeitssätze und die ersten Grundlagen der Rekursionstheorie, der Modelltheorie und der Mengenlehre.

Literatur:

1.)

H.-D. Ebbinghaus, J. Flum, W. Thomas: Einführung in die mathematische Logik (6. Auflage), Springer Spektrum, 2018.

2.)

M. Hils, F. Loeser: A first journey through logic, Student Mathematical Library Vol. 89, American Mathematical Society, 2019.

3.)

P.G. Hinman: Fundamentals of mathematical logic, A K Peters/CRC Press, 2005.

4.)

J.R. Shoenfield: Mathematical logic (Reprint of the 1973 second printing), A K Peters/CRC Press, 2010.

5.)

M. Ziegler: Mathematische Logik (2. Auflage), Birkhäuser, 2017.

6.)

M. Ziegler: Vorlesungsskript Mathematische Logik, verfügbar unter http://home.mathematik.uni-freiburg.de/ziegler/skripte/logik.pdf.

Inhalt:
Es geht um das Studium kommutativer Ringe und ihre Bedeutung für die Untersuchung von Nullstellenmengen polynomialer Gleichungssysteme in mehreren Veränderlichen über algebraisch abgeschlossenen Körpern. Die Vorlesung beginnt mit dem Hilbert’schen Nullstellensatz, Noether’schen Moduln und Ringen, Primidealen und irreduziblen Komponenten, Dimension, affinen Varietäten. Im weiteren Verlauf kommen wir zu projektiven und abstrakten Varietäten und dem Satz von Bezout.

Literatur:

1.)

Skript: http://home.mathematik.uni-freiburg.de/soergel/Skripten/XXKAG.pdf.

2.)

M.F. Atiyah, I.G. MacDonald: Introduction to Commutative Algebra, Addison-Wesley, 1969 (elektronisch verfügbar unter http://www.math.toronto.edu/jcarlson/A--M.pdf).

3.)

E. Kunz: Einführung in die Kommutative Algebra und Algebraische Geometrie, Springer, 1980.

4.)

G.R. Kempf: Algebraic Structures, Springer, 1995.

Inhalt:
Die Vorlesung baut auf den Kenntnissen auf, die in den Vorlesungen Analysis I und II über die euklidische Topologie von ℝ und ℝⁿ erworben wurden. Sie besteht aus zwei Teilen. Im ersten Teil wird die mengentheoretische Topologie bis zu dem Grad entwickelt, der für fortgeschrittene Vorlesungen in fast allen Bereichen der Mathematik nützlich ist. Der zweite Teil bietet eine Einführung in die Idee und in einige elementare Gegenstände der algebraischen Topologie (unter anderen die Begriffe der Homotopie, Fundamentalgruppe und Überlagerungen). Diese Begriffe spielen bereits in den elementaren Teilen der Analysis, Funktionentheorie und Geometrie eine wichtige Rolle.

Literatur:

1.)

J.R. Munkres: Topology (Second Edition), Prentice-Hall, 2000.

2.)

B. v. Querenburg: Mengentheoretische Topologie (3. Auflage), Springer, 2001.

Content:
The aim of this course is the application of the R programming environment to various topics of financial mathematics, among others are the calculation and visualization of interest rates, option prices, loss distributions and risk measures. Participants are expected to have attended the lecture “Futures and Options” before and to have some basic knowledge in using R as students of B.Sc. Mathematics usually acquire in the practical exercises of stochastics.

With help of these tools, we develop some programs for bootstrapping zero rates, pricing vanilla options in binomial trees and exotic options in time-continuous models via Monte Carlo methods. We also regard some aspects of hedging and convergence in this context. Further we discuss the implementation of risk measures, the sampling of loss distributions in elementary credit risk models. Depending on the time left, we may additionally discuss further topics in continuous-time interest theory and the simulation of (approximate) solutions to stochastic differential equations.

The course, which is taught in English, is offered for the second year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. (possibly also B.Sc.) Mathematics.

Literature:

1.)

J.C. Hull: Options, Futures, and other Derivatives (Tenth Edition), Prentice Hall, 2018.

2.)

T.L. Lai, H. Xing: Statistical Models and Methods for Financial Markets, Springer, 2008.

3.)

R.U. Seydel: Tools for Computational Finance (Sixth Edition), Springer, 2017.

4.)

Any introductory book to the R programming environment, e.g.,
J. Brown, D.J. Murdoch: A First Course in Statistical Programming with R (Second Edition), Cambridge University Press, 2016.

Inhalt:
In dieser Vorlesung werden Finanzmärkte in diskreter Zeit betrachtet. Dies ermöglicht einen Zugang ohne großen technischen Aufwand, so dass alle wesentlichen Konzepte betrachtet werden können. Die Vorlesung beginnt mit der Analyse von Handelsstrategien und leitet wichtige Beziehungen für die Arbitragefreiheit von Märkten ab. Als Beispiele werden das Binomialmodell, das Black-Scholes Modell und in größerer Allgemeinheit Zinsmärkte mit und ohne Ausfallrisiko betrachtet. Das Konzept von vollständigen und unvollständigen Märkten führt zur Suche von optimalen Absicherungsstrategien. Im Anschluss werden grundlegende Resultate zu konvexen und kohärenten Risikomaßen betrachtet.

Als Literatur wird die aktuelle Ausgabe des Buches Stochastic Finance von H. Föllmer und A. Schied empfohlen. Weitere Literaturhinweise werden in der Vorlesung gegeben.

Literatur:

1.)

H. Föllmer, A. Schied: Stochastic Finance (Fourth revised Edition), De Gruyter, 2016.

Content:
This course covers several mathematical aspects of deep learning. The focus will be on the approximation power of neural networks (shallow, deep, residual, recurrent, echo state, etc) in various function spaces (continuous, smooth, Sobolev, solutions of ODEs/PDEs/SDEs, etc). This topic shall be investigated from a variety of different perspectives using methods from functional analysis, harmonic analysis, differential geometry, probability, and stochastic analysis. The goal is to develop a theoretical understanding for the success of deep neural networks in many applications._____________________________________________________________________________________________________

Inhalt:
Als Modelle für viele physikalische Vorgänge, wie z.B. der Bestimmung einer Temperaturverteilung, der Beschreibung von Schwingungen von Membranen oder von Strömungen von Flüssigkeiten, treten partielle Differentialgleichungen auf.

Im ersten Teil der Vorlesung werden wir diese Grundgleichungen der Mathematischen Physik aus der Sicht der Kontinuumsmechanik herleiten sowie Grundprinzipien für die Modellierung von Materialeigenschaften kennenlernen.

Soweit es die Zeit erlaubt, werden wir danach die mathematische Theorie der stationären Stokesgleichungen entwickeln.

Literatur:

1.)

P. Chadwick: Continuum Mechanics: Concise Theory and Problems, Dover, 1999.

2.)

V. Girault, P.-A. Raviart: Finite Element Methods for Navier–Stokes Equations, Springer, 1986.

Inhalt:
Differentialgleichungen sind ein wichtiges mathematisches Werkzeug zur Beschreibung realer Vorgänge wie beispielsweise der Flugbahn eines Satelliten, der Entwicklung von Raub- und Beutetierpopulationen oder dem Abkühlen eines Körpers. In der Vorlesung werden verschiedene mathematische Modelle diskutiert und numerische Verfahren zur praktischen Lösung gewöhnlicher Differentialgleichungen der Form y′(t) = f(t,y(t)) untersucht.

Studierende, die die Veranstaltung im M.Sc.- oder M.Ed.-Studiengang nutzen wollen, können sie durch eine Projektarbeit und die begleitende Praktische Übung auf 9 ECTS-Punkte aufstocken.

Literatur:

1.)

S. Bartels: Numerik 3x9, Springer, 2016.

2.)

R. Plato: Numerische Mathematik kompakt (4. Auflage), Springer Vieweg, 2010.

3.)

W. Walter: Gewöhnliche Differentialgleichungen: Eine Einführung (7. Auflage), Springer, 2000.

Inhalt:
In der reellen algebraischen Geometrie geht es um Lösungen polynomialer Gleichungssysteme mit Koeffizienten aus dem Körper ℝ der reellen Zahlen (oder noch allgemeiner über sogenannten reell abgeschlossenen Körpern).

In dieser Vorlesung werden wir unter anderem das Hilbert’sche 17. Problem betrachten, welches 1926 von Artin bewiesen wurde:

Ist jedes reelle Polynom P in ℝ[x₁,…,x_n], welches an jedem n-Tupel aus ℝⁿ einen nichtnegativen Wert annnimmt, eine Summe von Quadraten rationaler Funktionen (d.h. Quotienten von Polynomen)?

Mit Hilfe des Satzes von Tarski-Seidenberg für Quantorenelimination in der Theorie reell abgeschlossenen Körper läßt sich die obige Frage leicht beantworten. Mit dieser Quantorenelimination werden die Grundlagen der o-Minimalität eingeführt.

Literatur:

1.)

A. Prestel: Vorlesungsskript Reelle Algebra, verfügbar unter http://www.math.uni-konstanz.de/~prestel/raskript.pdf.

2.)

L. van den Dries: Tame topology and o-minimal structures (London Mathematical Society Lecture Note Series), Cambridge University Press, 1998.

Content:
In physics, there exists the so-called correspondence principle, which states that on macro-scales, quantum mechanics should reduce to classical mechanics. This principle, yet not fully understood in physics, has a mathematical sibling. Consider a point on a manifold, X, that can move freely along the geodesics of X. Then the classical mechanical aspect of such motion relates to the geodesic flow on X, whereas the quantum description relates to the spectrum of the Laplace operator on X. The correspondence principle suggests that there exists a relationship between the properties of the geodesic flow on X on one hand and the spectral properties of X on the other hand.

The main aim of the course is to present such a relation for a very famous surface coming from number theory — the modular surface, that is the quotient of the hyperbolic plane, ℍ, by the modular group, PSL₂(ℤ). In particular, we want to connect its eigenfunctions, Maass forms, to the eigenfunctions of so-called transfer operators, that are constructed via the discretization of the geodesic flow on the modular surface. The key-words are: hyperbolic space and its isometries, discrete subgroups in PSL₂(ℤ), geodesics and geodesic flow, Laplace operator and its eigenfunctions, Gauss map and continued fractions, Bessel functions.

Literature:

1.)

J. Lewis, D. Zagier: Period functions for Maass wave forms I, Annals of Mathematics 153.1 (2001), 191–258.

2.)

S. Katok: Fuchsian groups, University of Chicago press, 1992.

Inhalt:
Die Veranstaltung bietet eine Einführung in die Programmierung mit theoretischen und praktischen Einheiten. Schwerpunkte der Veranstaltung sind:

• Logische Grundlagen der Programmierung
• Elementares Programmieren in C++
• Funktionsweise eines Prozessors
• Felder, Zeiger, abgeleitete Datentypen, (Datei-)Ein- und -ausgabe
• Algorithmik
• Programmieren und Visualisieren in MATLAB
• Funktionsweise eines Compilers
• Paralleles und objektorientiertes Programmieren
• Aspekte der IT-Kommunikation

Die praktischen Inhalte werden in der Programmiersprache C++ sowie in MATLAB erarbeitet. Die erworbene Kenntnisse werden anhand von Übungen und Hausaufgaben erprobt und vertieft.

Literatur:

1.)

S. Bartels, C. Palus: Einführung in die Programmierung (Vorlesungsskript)

2.)

R. Drechsler, A. Fink, J. Stopper: Computer, Springer 2017

3.)

T. Häberlein: Technische Informatik, Springer 2011

4.)

R. Klima, S. Selberherr: Programmieren in C, Springer 2010

5.)

G. Küveler, D. Schwoch: C/C++ für Studium und Beruf, Springer 2017

6.)

D. Logofatu: Einführung in C, Springer 2016

7.)

H. Müller, F. Weichert: Vorkurs Informatik, Springer 2017

8.)

M. von Rimscha, Algorithmen kompakt und verständlich, Springer 2014

9.)

R. Schneeweiß: Moderne C++ Programmierung, Springer 2012

10.)

G. Vossen, K.-U. Witt: Grundkurs Theoretische Informatik, Springer 2016

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung).

Leistungsnachweis:

• Teilnahme an dem Einführungsworkshop. Voraussichtlich etwa zwei halbe Tage; einen ungefähr in der ersten Vorlesungswoche und einen nach etwa vier Wochen. Näheres wird rechtzeitig bekanntgegeben.
• Regelmäßige Teilnahme an der Tutorenbesprechung.
• Zwei gegenseitige Tutoratsbesuche mit einem (oder mehreren) anderen Modulteilnehmer, welcher nach Möglichkeit die gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten, und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der Einführungsveranstaltung).

Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlbereich (im 2-Hf-Bachelor: „Optionsbereich“) angerechnet. Im 2-Hf-Bachelor ist es bei Wahl der Lehramtsoption eine über die 180 geforderter ECTS-Punkte hinausgehende Zusatzleistung. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet._________________________________________________

Inhalt:
Diese Veranstaltung thematisiert verschiedene Ansätze und Hintergründe zur Differenzierung und Heterogenität, mit besonderem Schwerpunkt auf sprachsensiblen Fachunterricht aus mathematikdidaktischer Sicht. Dabei werden viele didaktische Konstrukte aufgegriffen und mit der Unterrichtspraxis in Beziehung gesetzt. Die Veranstaltung richtet sich an alle Schulformen und thematisiert empirisch beforschte und praktisch relevante Herausforderungen und Entscheidungsfelder. Ihre Haupziele sind:

• Auseinandersetzung mit mathematikdidaktischer Forschung und Theorie zur Heterogenität,
• Kennenlernen praktischer Ansätze für Differenzierung, fokussierte Förderung und Inklusion.

Sie wird abgehalten werden als Mischung aus klassischem Seminar und Seminargestaltung durch die Studierenden.

Literatur:

1.)

T. Leuders, S. Prediger: Flexibel differenzieren und fokussiert fördern im Mathematikunterricht (2. Auflage), Cornelsen Scriptor, 2016.

Inhalt:
Diese drei zusammengehörigen Veranstaltungen bereiten auf das Anfertigen einer empirischen Masterarbeit in der Mathematikdidaktik vor. Das Angebot wird von allen Professorinnen und Professoren mit mathematikdidaktischen Forschungsprojekten der Sekundarstufe 1 und 2 gemeinsam konzipiert und von einem dieser Forschenden durchgeführt. Im Anschluss besteht das Angebot, bei einem/einer dieser Personen eine fachdidaktische Masterarbeit anzufertigen – meist eingebunden in größere laufende Forschungsprojekte.

In der ersten Veranstaltung findet eine Einführung in Strategien empirischer fachdidaktischer Forschung statt (Forschungsfragen, Forschungsstände, Forschungsdesigns). Studierende vertiefen ihre Fähigkeiten der wissenschaftlichen Recherche und der Bewertung fachdidaktischer Forschung.

In der zweiten Veranstaltung (im letzten Semesterdrittel) werden die Studierenden durch konkrete Arbeit mit bestehenden Daten (Interviews, Schülerprodukte, Experimentaldaten) in zentrale qualitative und quantitative Forschungsmethoden eingeführt.

Die Haupziele des Moduls sind:

• Fähigkeit zur Rezeption mathematikdidaktischer Forschung zur Klärung praxisrelevanter Fragen,
• Planung einer empirischen mathematikdidaktischen Masterarbeit.

Es wird abgehalten werden als Mischung aus Seminar, Erarbeitung von Forschungsthemen in Gruppenarbeit sowie aktivem Arbeiten mit Forschungsdaten. Literatur wird abhängig von den angebotenen Forschungsthemen innerhalb der jeweiligen Veranstaltungen angegeben werden.

Die Teile können auch in verschiedenen Semestern besucht werden, zum Beispiel Teil 1 im zweiten Mastersemester und Teil 2 in der Kompaktphase des dritten Mastersemesters nach dem Praxissemester.

 
Hinweis: M.Ed.-Studierende, die eine fachdidaktische Masterarbeit in Mathematik schreiben möchten, müssen das dreiteilige Modul Fachdidaktische Forschung absolvieren. Interessierte an einer fachdidaktischen Masterarbeit in Mathematik melden sich bitte zusätzlich bis zum Ende der Vorlesungszeit des Wintersemesters in der Abteilung für Didaktik. ______________________________________________________________________________

Inhalt:
In der praktischen Übung zur Numerik-Vorlesung sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

S. Bartels: Numerik 3x9, Springer, 2016.

Inhalt:
In der praktischen Übung zur Vorlesung über die Numerik für Differentialgleichungen sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

S. Bartels: Numerik 3x9, Springer, 2016.

Inhalt:
Die praktische Übung richtet sich an Hörerinnen und Hörer der Vorlesung Stochastik. Es werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der Vorlesung vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird das frei verfügbare Open-Source-Statistikprogramm R verwendet werden. Nach einer Einführung in R werden u.a. Verfahren der deskriptiven Statistik und graphischen Auswertung von Daten betrachtet, die numerische Erzeugung von Zufallszahlen erläutert sowie parametrische und nichtparametrische Tests und lineare Regressionsverfahren diskutiert. Vorkenntnisse in R und/oder Programmierkenntnisse werden dabei nicht vorausgesetzt.

Die praktische Übung ist für Studierende im (1-Hauptfach) B.Sc. Mathematik obligatorisch. Studierende des 2-Hauptfächer-Bachelors mit Lehramtsoption können selbstverständlich ebenfalls teilnehmen und die praktische Übung als Teil des Wahlpflichtmoduls Mathematik im Rahmen ihres Studiengangs verbuchen. Im Studiengang Master of Education kann die Veranstaltung als Mathematische Ergänzung belegt werden.

Für die eigene Arbeit mit R sollen die Laptops der Studierenden eingesetzt werden. Idealerweise sollte auf diesen bereits vor Beginn der Veranstaltung die dazu notwendige Software installiert werden. Genauere Anleitungen hierzu sowie entsprechende Links zum Download der kostenlosen Programme werden frühzeitig auf der o.g. Webseite bekannt gegeben.

Zu den einzelnen Lektionen der praktischen Übung wird ein ausführliches Skriptum bereitgestellt werden. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher zu R empfohlen werden.______________________________________________________________________________________

Inhalt:
Die lineare Algebra befasst sich mit linearen Abbildungen zwischen Vektorräumen. Eine lineare Abbildung V 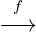W zwischen zwei Vektorräumen V,W kann man nun grafisch als „Pfeil“ zwischen zwei „Knotenpunkten“ darstellen: ∙ -→∙ .

Dieses Bild lässt sich verallgemeinern zu sogenannten „Köchern“ (engl. quiver) – bestehend eben aus einer Ansammlung von Pfeilen, z.B.

Eine Darstellung von einem Köcher ist nun gegeben durch die Wahl eines Vektorraums an jedem Knotenpunkt und eine lineare Abbildung für jeden Pfeil, z.B. für den linken Köcher

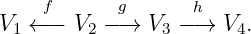
Um in die Theorie der Köcherdarstellungen einzusteigen, benötigt man tatsächlich nur Vorkenntnisse aus der linearen Algebra. Umso erstaunlicher ist es, dass Köcherdarstellungen nicht nur in der Darstellungstheorie, sondern auch in der algebraischen Geometrie bis hin zur mathematischen Physik weitreichende Anwendungen haben.

In diesem Proseminar wollen wir die Darstellungstheorie von Köchern Schritt für Schritt entwickeln. Am Ende des Proseminars behandeln wir den Satz von Gabriel über „darstellungs-endliche“ Köcher, der beschreibt, für welche Köcher sich beliebige Darstellungen aus endlich vielen unzerlegbaren Bausteinen zusammensetzen lassen. Erstaunlicherweise gibt es auch hier eine Verbindung zu anderen Teilen der Mathematik, nämlich zu Dynkin-Diagrammen, die in der Klassifizierung von Lie-Algebren eine fundamentale Rolle spielen.

Die Theorie der Köcherdarstellungen ist ein ausgezeichnetes Thema, um abstraktere Konzepte aus der Algebra (assoziative Algebren, Kategorien von Moduln, Anfänge der homologischen Algebra) kennenzulernen und dank der grafischen/diagrammatischen Herangehensweise ganz konkret zu veranschaulichen.

Literatur:

1.)

R. Schiffler: Quiver representations, CMS Books in Mathematics, Springer, 2014.

2.)

A. Kirillov Jr.: Quiver representations and quiver varieties, Graduate Studies in Mathematics 174, AMS, 2016.

Inhalt:
Differentialgleichungen sind Gleichungen, die sowohl Funktionen wie auch ihre Ableitungen enthalten. In vielen Modellen zur Beschreibung von Vorgängen in den Naturwissenschaften treten diese Differentialgleichungen auf. In diesem Proseminar werden wir uns sowohl mit der Theorie zur Existenz und Eindeutigkeit von Lösungen dieser Gleichungen als auch der Herleitung und Visualisierung expliziter Lösungen beschäftigen.

Literatur:

1.)

L. Beck: Gewöhnliche Differentialgleichungen Vorlesungsskript 2018, Universität Augsburg (elektronisch verfügbar unter https://assets.uni-augsburg.de/media/filer_public/ec/19/ec199b2d-22ea-4ec1-a3d4-1c7d914e34d3/ode.pdf).

2.)

W. Walter: Gewöhnliche Differentialgleichungen (7. Auflage), Springer, 2000.

3.)

R.L. Borrelli, C.S. Coleman: Differential Equations: A Modelling Perspective (Second Edition), Wiley, 2004.

Inhalt:
Die Spieltheorie modelliert strategisch-rationales Entscheidungsverhalten in Situationen, in denen mehrere Teilnehmer (Spieler) miteinander konkurrieren, mit Hilfe mathematischer Methoden. Sie ist daher originär ein Teilgebiet der Mathematik, hat aber vielfältige Anwendungsfelder, insbesondere in den Wirtschaftswissenschaften.

Ist ein Spiel durch seine Regeln wohldefiniert, stellt sich die Frage nach Existenz und Eindeutigkeit von optimalen Strategien für alle Spieler. Optimale Strategien sind dabei nicht unbedingt solche, die den eigenen Gewinn oder Nutzen maximieren, sondern solche, die den maximalen Verlust (worst case) bei ebenfalls optimal agierenden Mitspielern minimieren (Minimax-Probleme). Diese lässt sich mit spieltheoretischen Methoden beantworten; ein zentrales Lösungskonzept hierzu ist die Bestimmung von Gleichgewichtspunkten (sog. Nash-Gleichgewichte).

Ein klassisches Beispiel hierfür ist die Hirschjagd: Zwei Jäger, die mit ihren Gewehren nur jeweils einen Schuss abgeben können, gehen in einen Wald, in dem ein Hase und ein Hirsch leben. Den viel wertvolleren Hirsch können sie nur gemeinsam mit zwei Schüssen erlegen, den Hasen dagegen kann jeder von ihnen mit einem Schuss töten. Wie soll sich nun ein Jäger verhalten, dem zuerst der Hase über den Weg läuft?

Innerhalb des Proseminars sollen sowohl die mathematischen Grundlagen der Spieltheorie erarbeitet als auch einige Anwendungsbeispiele diskutiert werden. Eine genaue Themen- und Literaturliste wird bei der Vorbesprechung ausgegeben werden, zur Einstimmung und Orientierung können jedoch schon die u.g. Bücher dienen.

Literatur:

1.)

M. Maschler, E. Solan, S. Zamir: Game Theory, Cambridge University Press, 2013 (Kapitel elektronisch verfügbar unter https://ebookcentral.proquest.com/lib/ubfreiburg/detail.action?docID=1113044).

2.)

M. Osborne, A. Rubinstein: A Course in Game Theory, MIT Press, 1994 (elektronisch verfügbar unter http://ebour.com.ar/pdfs/A\%20Course\%20in\%20Game\%20Theory.pdf).

3.)

W. Schlee: Einführung in die Spieltheorie, Springer Vieweg, 2004.

Inhalt:
Alle Resultate der linearen Algebra gelten auch für andere Körper als ℝ oder ℂ. Die vielleicht exotischsten unter diesen sind die endlichen Körper, also solche, die nur aus einer endlichen Anzahl N von Elementen bestehen. Es zeigt sich, dass für jede Zahl N = p^l, wobei p eine Primzahl ist, ein (eindeutiger) endlicher Körper mit N Elementen existiert. Durch die Endlichkeit eignen sie sich besonders gut für Computerberechnungen und bilden die Basis so wichtiger Anwendungen wie Kodierung und Kryptographie. Ausserdem kann die Lösbarkeit beliebiger Gleichungen, wie z.B. der Fermatgleichung x^p + y^p = z^p, immer entschieden werden (Durchprobieren der endlich vielen Möglichkeiten!), aber man kann darüberhinaus nach der Anzahl der Lösungen fragen. Diese Anzahlen weisen überraschende und nicht-triviale Gesetzesmäßigkeiten auf. Das Proseminar soll unterschiedliche Aspekte endlicher Körper beleuchten, sowohl theoretische als auch praktische:

1.

Existenz von endlichen Körpern und grundlegende Eigenschaften

2.

Satz von Wedderburn: Nicht-Existenz von (echten) endlichen Schiefkörpern

3.

Gleichungen über endlichen Körpern

4.

Kodierung (Hamming Codes, Reed-Solomon Codes, ...)

5.

Kryptographie (Public-Key Kryptographie, RSA Verfahren, ...)

Literatur:

1.)

H. Kurzweil: Endliche Körper, Springer, 2008.

2.)

R. Lidl, H. Niederreiter: Finite Fields, Cambridge University Press, 1996.

3.)

N. Koblitz: A Course in Number Theory and Cryptography (Second Edition), Springer, 1994.

4.)

X.-d. Hou: Lectures on Finite Fields, AMS Graduate Studies in Mathematics, Volume 190, 2018.

5.)

K. Ireland, M. Rosen: A Classical Introduction to Modern Number Theory (Second Edition), Graduate Texts in Mathematics 84, Springer, 1990.

Inhalt:
In dem Seminar lesen wir klassische Artikel aus der Analysis, insbesondere den Artikel über harmonische Abbildungen, die die Verallgemeinerung von harmonischen Funktionen und Geodätischen sind.

Literatur:

1.)

C. Bandle: Isoperimetric inequalities, in: P.M. Gruber, J.M. Wills (Eds.): Convexity and Its Applications, Springer (1983), 30–48.

Inhalt:
Mathematische Knoten sind stetige injektive Abbildungen S¹ → S³ bzw. allgemeiner Sⁿ → Sⁿ⁺². Die Knotentheorie beschäftigt sich mit der Frage nach Invarianten, die direkt aus einem Knotendiagramm berechenbar sind und mit denen man verschiedene Knoten voneinander unterscheiden kann. Das Ziel des Seminars ist es, einige der topologischen und algebraischen Invarianten von Knoten kennenzulernen. In diesem Zusammenhang geht es natürlich auch darum, einige Grundbegriffe der algebraischen Topologie (Fundamentalgruppen, Homologie) kennenzulernen bzw. zu vertiefen. Einige algebraische Ausflüge zu Zopfgruppen, Hecke-Algebren und polynomialen Knoten runden das Seminar ab.

Literatur:

1.)

S. Bigelow: Braid groups and Iwahori–Hecke algebras, Proc. Symp. Pure Math. 74 (2006), 285—299.

2.)

A. Durfee, D. O’Shea: Polynomial knots, Preprint verfügbar unter https://arxiv.org/pdf/math/0612803.pdf.

3.)

A. Hatcher: Algebraic Topology, Cambridge University Press, 2002.

4.)

A. Kawauchi: A Survey of Knot Theory, Birkhäuser, 1996.

5.)

C. Kassel, V. Turaev: Braid groups, Graduate Texts in Mathematics 247, Springer, 2008.

6.)

D. Rolfsen: Knots and links, AMS Chelsea Publishing, 1976 (Reprint 2003).

7.)

A.R. Shastri: Polynomial representations of knots, Tohoku Math. J. 44 (1992), 11—17.

8.)

A. Shapiro, J.H.C. Whitehead: A proof and extension of Dehn’s lemma, Bull. Amer. Math. Soc. 64 (1958), 174-–178.

9.)

J.H.C. Whitehead: A certain open manifold whose group is unity, Quaterly J. Math. 6 (1935), 268—279.

Inhalt:
Differenzierbare Mannigfaltigkeiten bilden eine besonders interessante Klasse topologischer Räume. Kompakte Mannigfaltigkeiten lassen sich modulo Bordismus grob klassifizieren, dabei heißen zwei (orientierte) kompakte Mannigfaltigkeiten bordant, wenn sie gemeinsam den Rand einer (orientierten) kompakten Mannigfaltigkeit bilden. Bordismusgruppen werden durch die Pontryagin-Thom-Konstruktion als Homotopiegruppen von Thom-Räumen klassifizierender Räume beschrieben. Charakteristische Zahlen erlauben es, nicht bordante Mannigfaltigkeiten zu unterscheiden. Die Wu-Formeln stellen einen weiteren Zusammenhang zwischen charakteristischen Klassen modulo 2 und Steenrod-Quadraten her.

Wir stellen Grundlagen bereit wie Transversalitäts- und Einbettungssätze sowie Klassifikation von Vektorbündeln und charakteristische Klassen. Anschließend behandeln wir die Pontryagin-Thom-Konstruktion und beschreiben den orientierten und den komplexen Kobordismusring. Danach führen wir Steenrod-Quadrate ein betrachten Wu-Klassen.

Literatur:

1.)

T. Bröcker, T. tom Dieck: Kobordismentheorie, Lecture Notes in Mathematics 178, Springer, 1970.

2.)

J. Milnor: Topology from the differentiable viewpoint, University Press Virginia, 1965 (elektronisch verfügbar unter http://webmath2.unito.it/paginepersonali/sergio.console/Dispense/Milnor\%20Topology\%20from\%20\%23681EA.pdf).

3.)

J. Milnor, J. Stasheff: Characteristic Classes, Annals of Mathematical Studies 76, Princeton University Press, 1974 (elektronisch verfügbar unter http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.448.869&rep=rep1&type=pdf).

4.)

D. Quillen: Elementary Proofs of Some Results of Cobordism Theory using Steenrod Operations, Advances in Mathematics 7 (1971), 29–56.

5.)

R.E. Stong: Notes on Cobordism Theory, Princeton University Press, 1968 (elektronisch verfügbar unter https://www.maths.ed.ac.uk/~v1ranick/papers/stongcob.pdf).

Content:
String theory is one of the possible proposals for a description of quantum gravity, containing also possible other interactions. It deals with fundamental questions in relativity, like black holes, the nature of spacetime singularities, and maybe the history of the universe.

String theory has also fostered a fascinating interplay between mathematics and physics, such as in the study of Mirror Symmetry or in the stringy explanations for highly non-trivial mathematical facts such as Monstrous Moonshine or the ADE classification of singularities.

Due to its breadth and rapid development, string theory literature may appear intractable to the beginner. The aim of this seminar is to provide students with enough background in order to be able to tackle modern research. We shall do this via selected topics that lie at the foundation of string theory, and which include the classical bosonic string action, critical dimension, no-ghost theorems, and covariant quantization.

Literature:

1.)

B. Zwiebach: A First Course in String Theory (Second Edition), Cambridge University Press, 2009.

2.)

M.B. Green, J.H. Schwarz, E. Witten: Superstring Theory, Volume I, Cambridge University Press, 1987 (25th Anniversary Edition 2012).

3.)

K. Becker, M. Becker, J.H. Schwarz: String Theory and M-Theory—A Modern Introduction, Cambridge University Press, 2007 (available at http://www.nucleares.unam.mx/~alberto/apuntes/bbs.pdf).

4.)

T. Weigand: Lecture Notes Introduction to String theory, available at https://www.thphys.uni-heidelberg.de/~weigand/Skript-strings11-12/Strings.pdf.

Inhalt:
Etwa im Jahr 1980 definierte Shelah die Eigenschaft Properness für Forcinghalbordnungen. Properness ist eine Abschwächung der Antiketteneigenschaft (“c.c.c.”). Propere Forcings erhalten unter anderem ℵ₁ als Kardinalzahl und lassen sich mit abzählbaren Trägern iterieren.

In diesem Seminar studieren wir zuerst einige grundlegende Eigenschaften dieser Forcings und gehen dann zu Anwendungen in der Kombinatorik der Forcingnamen in Iterationen über, die besonders für die relative Konsistenz von Aussagen des Typus ∀x∃yφ(x,y) mit absolutem φ eine Rolle spielen. Es können Bachelor- und Masterarbeiten aus diesem Themenkreis vergeben werden.

Literatur:

1.)

U. Abraham: Proper Forcing, in: M. Foreman, A. Kanamori (Eds.): Handbook of Set Theory, Springer, 2010, 333–394.

2.)

K. Kunen: Set Theory. An Introduction to Independence Proofs, North Holland, 1980 (elektronisch verfügbar unter http://blacaman.tripod.com/cursos/pdf/2012-2_0941.pdf).

3.)

K. Kunen: Set Theory, College Publications, 2011.

4.)

S. Shelah: Proper Forcing, Lecture Notes in Mathematics 940, Springer, 1982.

5.)

S. Shelah: Proper and Improper Forcing (Second Edition), Perspectives in Mathematical Logic, Springer, 1997.

Content:
Combinatorial number theory has its origins in Schur’s theorem, which states that for any finite coloring of ℕ there are three elements x,y and z of the same color with x + y = z. A stronger version of Schur’s theorem was shown by Hindman:

Theorem. Any finite coloring of ℕ contains a subset all whose finite sums have the same color.

The purpose of this seminar is to provide an elementary proof of Hindman’s theorem using the Stone space of ultrafilters on ℕ, as well as other famous combinatorial theorems such as Waerden’s theorem on the existence of arbitrarily large monochromatic arithmetic progressions.

Literature:

1.)

V. Bergelson: Ultrafilters, IP sets, Dynamics, and Combinatorial Number Theory, in: V. Bergelson, A. Blass, M. Di Nasso, R. Jin (Eds.): Ultrafilters across mathematics, Contemporary Mathematics 530, AMS (2010), 23–47.

2.)

M. Di Nasso, I. Goldbring, M. Lupini: Nonstandard Methods in Ramsey Theory and Combinatorial Number Theory, Lecture Notes in Mathematics 2239, Springer, 2019.

Inhalt:
Im Seminar werden wir Techniken und Methoden zur Behandlung von Stokes- und Navier-Stokes-Gleichungen erarbeiten. Diese beinhalten sowohl theoretische als auch numerische Fragestellungen. Die behandelten Themen eignen sich als Grundlage für Bachelorarbeiten.______________________________________________________________________________________________

Inhalt:
Im Seminar werden lineare und nichtlineare Optimierungsaufgaben mit Nebenbedigungen und Variationsungleichungen behandelt. Neben theoretischen Existenzresultaten werden wir numerische Algorithmen zur Berechnung von Lösungen dieser Probleme kennenlernen. Wir werden uns unter anderem mit folgenden Themen beschäftigen: Optimalitätsbedingungen, Simplex-Verfahren, Penality-Methoden, Lagrange-Newton-Verfahren, Fixpunkt-Verfahren.
Die Seminarthemen sind besonders für 2-Hf-Bachelor- und GymPO-Studierende geeignet.

Literatur:

1.)

C. Geiger, C. Kanzow: Theorie und Numerik restringierter Optimierungsaufgaben, Springer, 2002.

Content:
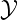Statistical Learning Theory has demonstrated its usefulness by providing the ground for developing successful and well-founded learning algorithms. The usual framework is as follows. We consider a space of possible inputs (instance space) and a space of possible outputs (label sets). The product space × 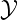is assumed to be measurable and is endowed with an unknown probability measure. Based on n independent input-output pairs (X₁,Y ₁),…, (X_n,Y _n) sampled according to this probability measure, the goal of a learning algorithm is to pick a function g in a space 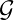of functions from to 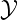in such a way that this function should capture as much as possible the relationship (which may not be of a functional nature) between the random variables X and Y .

In this seminar, we study this problem in a mathematically rigorous way, particularly focusing on recent learning algorithms. The theory of empirical processes will be shown to play a fundamental role in their analysis.

Das Seminar kann wahlweise in deutscher oder englischer Sprache abgehalten werden. Literatur wird in der Vorbesprechung bekanntgegeben werden.________________________________________________

Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik dienen.

Hinweise auf einführende Literatur werden in der Vorbesprechung (s.o.) gegeben.

Vorherige Anmeldung per E-Mail (sec@imbi.uni-freiburg.de) ist erwünscht._____________

Content:
In this course, we will study different statistical methods for analysing large data sets and apply these to different practical problems in finance and economics.
Topics may include:

• regression models (linear and logistic regression, estimation methods)
• model selection (in- and out-of-sample performance, regularization, cross validation)
• treatment effects (natural experiments, uncertainty quantification)
• classification methods (binary classification, multinomial logistic regression)
• networks (directed graphs, connectivity, page rank, Bayesian networks)
• dependence modelling (vine copulas, tail copulas)
• factor models (dimension reduction, latent variables, PCA)

Literature:

1.)

G. James, D. Witten, T. Hastie, R. Tibshirani: An Introduction to Statistical Learning, Springer, 2013.

2.)

T. Hastie, R. Tibshirani, J. Friedman: The Elements of Statistical Learning (Second Edition), Springer, 2009.

3.)

C. Bishop: Pattern Recognition and Machine Learning, Springer, 2006.

4.)

K.P. Murphy: Machine Learning. A Probabilistic Perspective, MIT Press, 2012.

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs im Idealfall als Vorbereitung auf die Master-Arbeit dient (im M.Sc. wie im M.Ed.).

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe, einem Oberseminar, Projektseminar …) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im M.Ed. und im Modul „Mathematik“ des M.Sc. gibt es eine mündliche Abschlussprüfung über den Stoff des Lesekurses, im Vertiefungsmodul des M.Sc. eine mündliche Abschlussprüfung über sämtliche Teile des Moduls. Ein Lesekurs zur Vorbereitung auf die Master-Arbeit kann im M.Sc. auch im Wahlmodul angerechnet werden (ohne Prüfung, nur Studieneistung).

Im M.Sc.-Studiengang ist daran gedacht, dass Sie einen, maximal zwei Lesekurse absolvieren.

Content:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology or mathematical physics or a mix thereof.

The precise topic will be chosen at the end of the preceeding semester. The program will be made available via our web site.

The level is aimed at our doctoral students. Master students are very welcome to participate as well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. Annette Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17:00 Uhr im Hörsaal II in der Albertstraße 23b statt.

Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Ernst-Zermelo-Straße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/