Lehrveranstaltungen

Inhalt:
Die Funktionentheorie ist ein klassisches Gebiet der höheren Mathematik und befasst sich mit der Differential- und Integralrechnung für komplex differenzierbare Funktionen in einer komplexen Veränderlichen. Diese können natürlich auch als Funktionen zweier reeller Veränderlichen aufgefasst werden und sind dann automatisch nicht nur beliebig oft stetig differenzierbar, sondern genügen außerdem den Cauchy-Riemannschen Differentialgleichungen. Die überraschenden Ergebnisse der Funktionentheorie können auf die besonders schönen Eigenschaften dieser Differentialgleichungen zurückgeführt werden. Zum Beispiel sind komplex differenzierbare Funktionen immer analytisch, können also lokal als Potenzreihen dargestellt werden. Außerdem ist eine komplex differenzierbare Funktion durch erstaunlich wenig Daten eindeutig bestimmt: Ihre Werte auf einer Kreisscheibe sind schon durch ihre Werte auf dem Rand eindeutig festgelegt. Die vielen schönen Eigenschaften komplex differenzierbarer Funktionen erlauben zahlreiche Anwendungen in verschiedensten Gebieten der Mathematik und Physik.

Zentrale Themen der Vorlesung sind die Grundlagen der Funktionentheorie, also insbesondere Cauchy-Riemannsche Differentialgleichungen, der Cauchysche Integralsatz, die Cauchysche Integralformel, Maximumprinzip und Residuensatz. Sofern die Zeit es erlaubt, werden außerdem Anwendungen in der Zahlentheorie angesprochen, z.B. der Beweis des Primzahltheorems.

Literatur:

1.)

K. Jänich, Funktionentheorie, Springer, 2008

2.)

E. Freitag, R. Busam, Funktionentheorie, Springer, 2006

3.)

S. Lang, Complex Analysis, Springer, 1999

4.)

R. Remmert, Funktionentheorie I, Springer, 1984

Inhalt:
In der linearen Algebra mögen Sie gesehen haben, wie es gelingt, mit den Mitteln der Algebra unseren Anschauungsraum zu modellieren. In dieser Vorlesung soll umgekehrt eine geometrische Modellierung des Anschauungsraums vorgestellt werden und es soll gezeigt werden, wie sie zu Körpern und Vektorräumen führt. Durch das Hinzufügen unendlich ferner Punkte gelangt man zur projektiven Geometrie, Abschwächungen der Annahmen führen zur hyperbolischen Geometrie.

Wir besprechen weiter Isometrien euklidischer Räume sowie endliche Untergruppen der Isometriegruppe des dreidimensionalen euklidischen Raums und platonische Körper.

Die Eulersche Polyederformel soll nur propädeutisch behandelt werden, für eine mathematisch exakte Formulierung mit Beweis wird die Zeit nicht ausreichen. Die Geometrie der Kegelschnitte wird auch nur vergleichsweise kurz behandelt werden.

Wenn Zeit bleibt, will ich noch auf Möbiustransformationen und das Apollonische Problem eingehen.

Literatur:

1.)

Wolfgang Soergel, Skriptum lineare Algebra I

2.)

Wolfgang Soergel, Skriptum lineare Algebra II

Inhalt:
Es wird eine Einführung in die klassische Differentialgeometrie im Euklidischen Raum gegeben. Im Vordergrund steht dabei die Frage, was die Krümmung einer Kurve bzw. Fläche ist und welche geometrische Bedeutung sie für die Kurve bzw. Fläche als Ganzes hat. Entlang der Theorie werden zahlreiche Beispiele behandelt. Gegen Ende der Vorlesung werden abstrakte, also nicht in den ℝ³ eingebettete Flächen betrachtet, zum Beispiel die hyperbolische Ebene.

Für Studierende im Staatsexamen ist die Vorlesung sehr geeignet.

Literatur:

1.)

C. Bär: Elementare Differentialgeometrie, de Gruyter 2001.

2.)

M. P. do Carmo: Differential Geometry of Curves and Surfaces, Prentice Hall 1976.

3.)

W. Klingenberg: Eine Vorlesung über Differentialgeometrie, Springer Verlag 1973.

Inhalt:

Die lineare Funktionalanalysis verwendet Konzepte der linearen Algebra wie Vektorraum, linearer Operator, Dualraum, Skalarprodukt, adjungierte Abbildung, Eigenwert, Spektrum, um Gleichungen in unendlichdimensionalen Funktionenräumen zu lösen. Dazu müssen die algebraischen Begriffe durch topologische Konzepte wie Konvergenz, Vollständigkeit, Kompaktheit etc. geeignet erweitert werden. Die Vorlesung wird vor allem Aspekte behandeln, die für die Lösung von linearen und nichtlinearen partiellen Differentialgleichungen relevant sind. Dazu gehört das Konzept des Sobolevraums sowie die Lösung von elliptischen Randwertproblemen mit Hilbertraummethoden.

Literatur:

1.)

Alt, H.W. : Lineare Funktionalanalysis (5. Auflage), Springer 2006.

2.)

Werner, D., Funktionalanalysis, Springer 2007

3.)

Brezis, H., Functional Analysis, Sobolev Spaces and Partial Differential Equations Springer 2011

Inhalt:
Zahlentheorie beschäftigt sich mit den Eigenschaften der ganzen Zahlen. Fragen nach der Lösbarkeit von Gleichungen (z.B. x³ + y³ = z³) führen schnell dazu, dass man den Zahlbereich vergrössert (z.B. x³ + y³ = (x + y)(x + ρy)(x + ρ²y) für ρ = e^2πi∕3). Algebraische Zahlentheorie konzentriert sich auf diese Verallgemeinerungen von ℤ und ihre Eigenschaften.

Wir wollen diese Zahlbereiche definieren und ihre grundlegenden Eigenschaften studieren. Sie verhalten sich zum Teil ähnlich zu den ganzen Zahlen, aber es treten auch neue Phänomene auf. Betrachtet man zum Beispiel den Zahlbereich

so gibt es keine eindeutige Primfaktorzerlegung mehr, wie man an den beiden wesentlich verschiedenen Zerlegungen

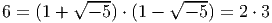
sehen kann. Wichtigste Ziele sind die Endlichkeit der Klassenzahl (sie misst, wie sehr die Eindeutigkeit der Primfaktorzerlegung fehlschlägt) und der Dirichletsche Einheitensatz.

Literatur:

1.)

J. Neukirch, Algebraische Zahlentheorie

2.)

S. Lang, Algebraic Number Theory

3.)

P. Samuel, Algebraic Theory of Numbers

4.)

A. Weil, Basic Number Theory

Inhalt:
In dieser Vorlesung geht es um die Topologie differenzierbarer Mannigfaltigkeiten. Das Idealziel wäre es, alle differenzierbaren Mannigfaltigkeiten bis auf Diffeomorphismen zu klassifizieren, aber hierbei stößt man auf unüberwindliche Hindernisse. Wir werden uns daher damit begnügen, Manngifaltigkeiten aus verschiedenen Perspektiven zu betrachten und am Ende relativ grob zu klassizifizieren.

Wir führen differenzierbare Mannigfaltigkeiten ein und beweisen zunächst einige grundlegende Resultate wie den Whitneyschen Einbettungssatz und den Transversalitätssatz.

Dann betrachten wir de Rham-Kohomologie, Vektorbündel und charakteristische Klassen und schließlich Kobordismen. Zu den Anwendungen gehören beispielsweise der Brouwersche Fixpunktsatz, der Satz vom Igel und der Satz von Borsuk-Ulam.

Wenn Zeit bleibt, können wir anschließend zum Beispiel exotische Sphären konstruieren. Diese Räume sind homöomorph, aber nicht diffeomorph zur Standardsphäre.

Literatur:

1.)

M. W. Hirsch, Differential Topology, Grad. Text Math. 33 Springer, New York, 1976

2.)

J. Milnor, Topology from the differentiable viewpoint, The University Press of Virginia, Charlottesville, 1965

Weitere Literatur wird in der Vorlesung angegeben.__________________________________________________________

Inhalt:
Commutative Algebra is a general version of Linear Algebra that applies to all commutative rings rather than just fields. Vector spaces are then replaced by the concept of modules. These concepts and their variations appear in many places in Geometry and in Analysis, however the main field of application is Number Theory and Algebraic Geometry, seen as the study of solution sets of polynomial equation systems. We will therefore develop the formal theory, and at the same time work out the basics of Algebraic Geometry. As Eisenbud put it: Commutative Algebra is best understood with knowledge of the geometric ideas that have played a great role in its formation, in short, with a view towards algebraic geometry.”

The course will be taught in English.

Literatur:

1.)

Atiyah, MacDonald: Introduction to commutative algebra

2.)

Mumford: The red book of varieties and schemes

3.)

Shafarevich: Basic algebraic geometry

4.)

Eisenbud: Commutative Algebra with a View Toward Algebraic Geometry

5.)

Fulton: Algebraic Curves,  http://www.math.lsa.umich.edu/wfulton/CurveBook.pdf

Inhalt:
Dies ist eine Einführung in die mathematische Logik. Wir werden den Begriff eines mathematischen Beweises präzisieren. Für den festgelegten Beweisbegriff beantworten wir dann folgende Fragen: Von welchen (nicht beweisbaren) Grundprinzipien geht man aus? Kann man das Nachprüfen oder gar das Finden von Beweisen geeigneten Computern überlassen? Gegenstände der Vorlesung sind der Gödel’sche Vollständigkeitssatz und die Gödel’schen Unvollständigkeitssätze und die ersten Grundlagen der Rekursionstheorie, der Modelltheorie und der Mengenlehre.

Literatur:

1.)

H.-D. Ebbinghaus, J. Flum, W. Thomas, Einführung in die mathematische Logik, Spektrum Verlag, 2007.

2.)

Peter G. Hinman. Fundamentals of mathematical logic. A K Peters, Ltd., Wellesley, MA, 2005. xvi+878 pp

3.)

Joseph R. Shoenfield, Joseph, Mathematical logic. Reprint of the 1973 second printing. Association for Symbolic Logic, Urbana, IL; A K Peters, Ltd., Natick, MA, 2001.

4.)

Ziegler, Skript „Mathematische Logik”.

5.)

Martin Ziegler, Mathematische Logik, 2. Auflage, Birkhäuser, 2017.

Inhalt:
Im Anschluss an die Vorlesung stochastische Prozesse befasst sich diese Vorlesung ausführlich mit finanzmathematischen Fragestellungen. Zu Beginn betrachten wir stochastische Integration bezüglich Semimartingalen und Fundamentalsätze zur Freiheit von Arbitrage. Danach widmen wir uns einer Auswahl weiterführender Themen wie Zinsmodellierung, Modellierung von Aktien- und Optionspreisen mit stochastischer Volatilität, Kreditrisikomodellierung, Bewertung amerikanischer Optionen, und Modellrisiko.____________________________________________________________

Inhalt:
Gewöhnliche Differentialgleichgungen sind Gleichungen für Funktionen und deren Ableitungen, die nur von einer reellen Variablen abhängen. Diese dienen als mathematisches Modell z.B. für die Berechnung von Flugbahnen (Anfangswertproblem) oder die Verbiegung von eindimensionalen Balken (Randwertproblem). In der Vorlesung werden numerische Algorithmen entwickelt um Anfangswert-oder Randwertprobleme zu lösen.

Literatur:

1.)

S. Bartels: Numerik 3x9. Springer 2016

2.)

R. Plato: Numerische Mathematik kompakt. Vieweg 2000

3.)

W. Walter: Gewöhnliche Differentialgleichungen: Eine Einführung. Springer 2000

Inhalt:
In dieser Vorlesung werden wir den mathematischen Modellierungsprozess an mehreren Beispielen demonstrieren. Am Anfang steht jeweils eine Frage aus den Anwendungen wie z.B. Physik, Biologie, Chemie oder Wirtschaft. Durch Definition geeigneter Größen wird diese Frage dann in die Sprache der Mathematik übersetzt, z.B. in eine Gleichung, gewöhnliche Differentialgleichung oder auch eine partielle Differentialgleichung. In der Vorlesung werden wir Beispiele zu den Themen Wärmeleitung, Diffusion, Schwingungen von Stäben und Membranen, Strömungen von reibungsfreien und reibunsbehafteten Strömungen, Kapillarität, Populationsdynamik, Elastizität und Verkehrssimulation besprechen.

Literatur:

1.)

C. Eck et al., Mathematische Modellierung, Springer 2017

2.)

A. Jüngel, Mathematische Modellierung mit Differentialgleichungen, unkorrigiertes Vorlesungsskript 2003

Inhalt:
Das Ziel der Vorlesung ist ein Überblick über die modernen Entwicklungen zum dritten Hilbertschen Problem – der Klassifikation von Polytopen (in euklidischen, hyperbolischen und sphärischen Geometrien) bis auf Scherenkongruenz. Die Vorlesung beginnt mit der notwendigen Elementargeometrie und den Definitionen der Dehn-Invariante und der Polytopalgebra. Der wesentliche Teil der Vorlesung wird sich damit beschäftigen, wie die Algebra der Polytope in hyperbolischen und sphärischen Räumen durch Homologie von Isometriegruppen bzw. K-Theorie beschrieben werden kann. Die zentrale Vermutung von Goncharov verbindet dann die Polytopalgebra mit der Galoisgruppe der gemischten Tate-Motive über ℂ. Dadurch kann die zentrale Frage zur Klassifikation von Polytopen (Sind Scherenkongruenzklassen durch Volumen und Dehn-Invariante eindeutig gekennzeichnet?) in Fragen zur K-Theorie (Injektivität des Regulators) übersetzt werden. Zum Abschluß werden die zahlentheoretischen Konsequenzen (Verbindungen zwischen speziellen Werten von L-Funktionen, Polylogarithmen und Volumina von Simplizes) diskutiert. In Ermangelung geeigneter Literatur wird es ein Vorlesungsskript geben (in Englisch).___________________________________________________________________________________________

Inhalt:
The aim of this course is the application of the R programming environment to various topics of financial mathematics, among others are the calculation and visualization of interest rates, option prices, loss distributions and risk measures. Participants are expected to have some basic knowledge in using R as students of B.Sc. Mathematics usually acquire in the practical exercises of stochastics.

With help of these tools, we develop some programs for bootstrapping zero rates, pricing vanilla options in binomial trees and exotic options in time-continuous models via Monte Carlo methods. We also regard some aspects of hedging and convergence in this context. Further we discuss the implementation of risk measures, the sampling of loss distributions in elementary credit risk models. Depending on the time left, we may additionally discuss the simulation of (approximate) solutions to stochastic differential equations.

The course, which is taught in English, is offered for the second year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. (possibly also B.Sc.) Mathematics.

Literatur:

1.)

Hull, J.C.: Options, Futures, and other Derivatives, 7th ed., Prentice Hall, 2009

2.)

Lai, T.L., Xing, H.: Statistical Models and Methods for Financial Markets, Springer, 2008

3.)

Seydel, R.U.: Tools for Computational Finance, 4th ed., Springer, 2009

4.)

Any introductory book to the R programming environment, e.g.,
Brown, J., Murdoch, D.J.: A First Course in Statistical Programming with R, Cambridge University Press, 2007

Inhalt:
Eine Markov-Kette ist ein sogenannter gedächtnisloser stochastischer Prozess in diskreter Zeit und mit diskretem Zustandsraum. Trotz ihrer Einfachheit sind Markov-Ketten interessante mathematische Objekte, mit denen sich eine Vielzahl von Phänomenen modellieren lassen.

Das Ziel der Vorlesung ist eine Einführung in die Theorie der Markov-Ketten; es werden unter anderem folgende Themen behandelt:

• Markov-Eigenschaft, Übergangswahrscheinlichkeiten
• Irreduzibilität, Rekurrenz und Transienz
• Ergodizität, stationäre Verteilungen, Kopplungsmethoden
• Zufällige Irrfahrten, elektrische Netzwerke

Literatur:

1.)

A. Klenke: Wahrscheinlichkeitstheorie. Springer, 2013

2.)

S.I. Resnick: Adventures in Stochastic Processes. Birkhäuser, 1992

Inhalt:
Im heutigen Informationszeitalter werden vermehrt auch private und sensible Daten über jeden Einzelnen von uns (etwa medizinische Daten oder Nutzerverhalten von Smartphones) erhoben, elektronisch weiterverarbeitet und analysiert. Dem steht ein wachsendes Bedürfnis nach Wahrung der Privatsphäre sowie nach strengeren Datenschutzregelungen gegenüber. Die Computerwissenschaften, insbesondere im Bereich der Datenbanksysteme, beschäftigen sich seit geraumer Zeit mit der Frage, wie die Privatsphäre des Einzelnen geschützt werden kann, ohne auf die Fülle an Informationen in den erhobenen Daten verzichten zu müssen. Die Entwicklung optimaler statistischer Verfahren unter gleichzeitiger Berücksichtigung der Privatsphäre der Individuen befindet sich dagegen noch in den Anfängen.

In dieser Spezialvorlesung beschäftigen wir uns insbesondere mit dem Konzept der ‘differential privacy’ und mit Fragen von minimax optimaler Schätzung basierend auf privatisierten Daten. Ganz im Sinne der forschungsgeleiteten Lehre werden zum Teil noch im Entstehen befindliche und unveröffentlichte Resultate des Dozenten diskutiert. Es bestehen zahlreiche Anknüpfungspunkte für mögliche Masterarbeiten und Dissertationsprojekte.

Literatur:

1.)

M. Ye and A. Barg: Asymptotically Optimal Private Estimation under Mean Square Loss, arXiv:1708.00059, 2017.

2.)

J. C. Duchi and M. I. Jordan and M. J. Wainwright: Local Privacy, Data Processing Inequalities, and Minimax Rates, arXiv:1302.3203, 2014.

3.)

L. Wasserman and S. Zhou: A Statistical Framework for Differential Privacy, Journal of the American Statistical Association, Vol. 105, No. 489, 2010.

Inhalt:
Die Vorlesung baut auf den Kenntnissen auf, die in den Vorlesungen Analysis I, II über die Topologie von ℝ und ℝⁿ erworben wurden. In dieser Vorlesung wird die mengentheoretische Topologie bis zu dem Grad entwickelt, der für fortgeschrittene Vorlesungen in fast allen Bereichen der Mathematik nützlich ist. Insbesondere geht es um Verallgemeinerungen von Begriffen wie Stetigkeit oder Kompaktheit auf nicht metrische Räume. Diese Begriffe spielen schon in den elementaren Teilen der Analysis, Funktionentheorie und Geometrie eine wichtige Rolle.

Literatur:

1.)

B. von Querenburg : Mengentheoretische Topologie, 3. Auflage 2001, Springer

2.)

J.R. Munkres: Topology, 2. ed,Upper Saddle River, NJ [u.a.]: Pearson Education International, Prentice Hall, 2000

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich (im Zwei-Hauptfächer-Bachelor: „Optionsbereich“) angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Leistungsnachweis:

• Teilnahme am Workshop „Fit für das Tutorat“ am Mittwoch, 11. April 2018, von 09:00 Uhr bis 16:30 Uhr im Seminarraum 404 im Mathematischen Institut (bei Tutoraten zu Vorlesungen, die nicht mehr zur Studieneingangsphase gerechnet werden können, Teilnahme nur nach Rücksprache mit der Dozentin, Frau Lickert – ersatzweise kann ein Erfahrungsbericht über das Tutorat geschrieben werden);
• Teilnahme an der Einführungsveranstaltung (voraussichtlich in der zweiten oder dritten Vorlesungswoche; Termin wird kurzfristig im Vorlesungsverzeichnis bekanntgegeben);
• regelmäßige Teilnahme an der Tutorenbesprechung;
• zwei gegenseitige Tutoratsbesuche mit einem anderen Modulteilnehmer, welcher nach Möglichkeit die gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der Einführungsveranstaltung).

In Ermangelung eines passenden Wahlbereichs kann das Modul im Lehramtsstudiengang in dieser Form leider nicht angeboten werden. Im 2-Hauptfächer-Bachelor ist es bei Wahl der Lehramtsoption eine über die 180 geforderter ECTS-Punkte hinausgehende Zusatzleistung.__________________________________________________________________________________________________

Einführung in die Fachdidaktik der Mathematik

Mathematik-Studierende im polyvalenten Zwei-Hauptfächer-Bachelor-Studiengang, die die Lehramtsoption wählen, müssen im Optionsbereich u.a. das Fachdidaktikmodul Einführung in die Fachdidaktik der Mathematik (5 ECTS-Punkte) absolvieren.

Studierende im Zwei-Hauptfächer-Bachelor-Studiengang, die nicht die Lehramtsoption wählen oder sich im Nachhinein dagegen entscheiden, können das Modul als Berufsfeldorientierte Kompetenzen (BOK) anrechnen lassen.

Dieses Modul wird im Sommersemester 2018 auf folgende Weise angeboten:

Es besteht aus der eigentlich für das Lehramt nach GymPO angebotene Veranstaltung Didaktik der Geometrie und Stochastik (Vorlesung mit Übungen; 2,5 SWS, 3 ECTS), die durch ein zusätzliches „eingebettetes Seminar“ auf 5 ECTS-Punkte aufgewertet wird.

Ab dem Wintersemester 2018/19 werden die im Lehramt nach GymPO vorgesehenen Veranstaltungen Didaktik der Algebra und Analysis und Didaktik der Geometrie und Stochastik nicht mehr angeboten. Die Veranstaltung Einführung in die Fachdidaktik der Mathematik soll in jedem Semester angeboten werden.

Inhalt:
Unterricht außerhalb des Klassenzimmers. Sei es auf dem Pausenhof, auf der Wiese vor der Schule, im Wald, in einem Mathe-Camp oder im Schullandheim. In diesem Seminar werden solche Lernumgebungen bzw. Erlebnisräume „jenseits des Klassenzimmers“ in Kleingruppen entworfen und durchgeführt.

Konkret:

• Handlungs- und erlebnisorientierte Didaktik, konstruktivistische und subjektive Didaktik
• Rollenverständnis (Rollen des Lehrers, Wechsel von Rollen, Rollenbelegung von mathematischen Inhalten)
• Gruppendynamik (Gruppenentwicklungsphasen) und Gruppenunterricht, innere Struktur von Gruppen für das Fach Mathematik (Farbgruppen, Rollenverständnis)
• Kommunikation (Quadratische Nachrichten, inneres Team, Feedback, Elterngespräche konstruktiv führen, Umgang mit mathematisch belasteten Schülern)
• Konkretes Erleben verschiedener Lernumgebungen der Kleingruppen
• Studierende entwerfen eigene Erlebnisräume, die anschließend durchspielt werden.
• Mathematisierung eines Klettergartens

Hinweis zur Unterkunft: Das Schwarzhornhaus bei Waldstetten (http://www.schwarzhornhaus.de/) ist ein Selbstversorgerhaus. Es wird gemeinsam gekocht. Übernachtet wird in Mehrbettzimmern (Schullandheim). Eigenen Bettbezug bitte mitbringen. _________________________________________________________

Weitere Fachdidaktik-Seminare

Als weiteres Angebot an Fachdidaktik-Seminaren öffnet die Pädagogische Hochschule (PH) zwei ihrer Seminare für Lehramtsstudierende (GymPO).

Die Anmeldung erfolgt per Listeneintrag im Sekretariat der Abteilung für Didaktik der Mathematik. Pro Seminar stehen 10 Plätze zur Verfügung.

Beachten Sie den um eine Woche früheren Vorlesungsbeginn der Veranstaltungen an der Pädagogischen Hochschule.

Fachdidaktische Vernetzung
(Prof. Dr. L. Holzäpfel, Zeit: Mi 10–12 Uhr, Ort: PH, KG 4, Raum 301)

Die Lehrveranstaltung Fachdidaktische Vernetzung bildet – entsprechend ihrem Titel – Schnittstellen zu den Bereichsdidaktiken der Mathematik einerseits und zur Forschungsperspektive andererseits (horizontale Vernetzung). Gleichzeitig stellt sie die Anbindung an die Bildungswissenschaften her und bildet die Brücke zur Praxis (vertikale Vernetzung). Abhängig davon, ob die Veranstaltung vor oder nach dem Semesterpraktikum besucht wird, hat sie vor- bzw. nachbereitenden Charakter.

Während eine traditionelle Einführung in die Mathematikdidaktik am Beginn des Studiums steht, um dort die zentralen mathematikdidaktischen Begriffe und Konzepte zu vermitteln, diese dann aber oft beliebig und zusammenhangslos wirken und ihre Bedeutung nicht zum Tragen kommt, steht in der Veranstaltung Fachdidaktische Vernetzung der Überblick über sämtliche in der Mathematikdidaktik relevanten Themen im Fokus. Behandelt werden u.a. die Themen Kompetenzorientierung, Sinnstiftung, Anwendungsorientierung, Modellieren, Erkunden – Systematisieren – Sichern, Vertiefen/Üben, Begriffsbilden, Problemlösen, Diagnose, Differenzieren und Kooperatives Lernen.

Didaktik der Stochastik
(Prof. Dr. K. Maaß, Zeit: Do 12–14 Uhr, Ort: PH, KG 4, Raum 207)

Die Veranstaltung Didaktik der Stochastik greift wichtige Fragen des Statistik- und Stochastikunterrichts der Sekundarstufe I auf. An konkreten Beispielen für den Unterricht wird besprochen, wie der Unterricht für die Schülerinnen und Schüler relevant, spannend, forschend und experimentell gestaltet werden kann. Besondere Berücksichtigung findet dabei, welche Ziele mit dem Unterricht insgesamt sowie mit einzelnen Fragestellungen und Aufgaben erreicht werden können und wie Fehlvorstellungen von Schülerinnen und Schülern vorgebeugt werden kann.

Die Vorlesung richtet sich an Studierende für das Lehramt in der Sekundarstufe I und II und ist zweistündig. Eine Vor- und Nachbereitung der Vorlesung wird erwartet.

Inhalt:
In der praktischen Übung zur Numerik-Vorlesung sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

S. Bartels: Numerik 3x9. Springer, 2016.

2.)

R. Plato: Numerische Mathematik kompakt. Vieweg, 2006.

3.)

R. Schaback, H. Wendland: Numerische Mathematik. Springer, 2004.

4.)

J. Stoer, R. Burlisch: Numerische Mathematik I, II. Springer, 2007, 2005.

5.)

G. Hämmerlin, K.-H. Hoffmann: Numerische Mathematik. Springer, 1990.

6.)

P. Deuflhard, A. Hohmann, F. Bornemann: Numerische Mathematik I, II. DeGruyter, 2003.

Inhalt:
In diesem Praktikum werden die in der Vorlesung ”Numerik für Differentialgleichungen” besprochenen Algorithmen implementiert, um numerische Näherungslösungen für Anfangs-und Randwertprobleme zu berechnen und zu visualisieren. Grundlage für die Programmierung sind die Programmiersprache C, C++ und MATLAB.

Literatur:

1.)

S. Bartels: Numerik 3x9. Springer 2016

Inhalt:
Die praktische Übung richtet sich an Hörerinnen und Hörer der Vorlesung Stochastik. Es werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der Vorlesung vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird das frei verfügbare Open-Source-Statistikprogramm R verwendet werden. Nach einer Einführung in R werden u.a. Verfahren der deskriptiven Statistik und graphischen Auswertung von Daten betrachtet, die numerische Erzeugung von Zufallszahlen erläutert sowie parametrische und nichtparametrische Tests und lineare Regressionsverfahren diskutiert. Vorkenntnisse in R und/oder Programmierkenntnisse werden dabei nicht vorausgesetzt.

Die praktische Übung ist für Studierende im (1-Hauptfach) B.Sc. Mathematik obligatorisch. Studierende des 2-Hauptfächer-Bachelors mit Lehramtsoption können selbstverständlich ebenfalls teilnehmen und die praktische Übung als Teil des Wahlpflichtmoduls Mathematik im Rahmen ihres Studiengangs verbuchen.

Für die eigene Arbeit mit R sollen die Laptops der Studierenden eingesetzt werden. Idealerweise sollte auf diesen bereits vor Beginn der Veranstaltung die dazu notwendige Software installiert werden. Genauere Anleitungen hierzu sowie entsprechende Links zum Download der kostenlosen Programme werden frühzeitig auf der o.g. Webseite bekannt gegeben.

Zu den einzelnen Lektionen der praktischen Übung wird ein ausführliches Skriptum bereitgestellt werden. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher zu R empfohlen werden.______________________________________________________________________________________

Praktische Übung im 2-Hauptfächer-Bachelor

Ab Sommersemester 2018 soll der BOK-Kurs „Einführung in die Programmierung für Studierende der Naturwissenschaften“ für Studierende des Fachs Mathematik im 2-Hauptfächer-Bachelor als Praktische Übung für den Wahlpflichtbereich angerechnet werden können.

Die genaue Abwicklung über HISinOne muss noch geklärt werden; die Belegung wird aber nicht über das ZfS erfolgen.

Inhalt:
 
Charles-François Sturm und Joseph Liouville schrieben um 1830 eine Reihe von Artikeln über eine Klasse reeller gewöhnlicher Differentialgleichungen zweiter Ordnung, welche heute Sturm-Liouville Probleme genannt wird. Sie waren die ersten, die in großem Stile Eigenschaften von Lösungen studierten, die man oft nicht mit einem analytischen Ausdruck direkt hinschreiben kann. Der Einfluss dieser Arbeiten geht weit über ihr eigentliches Thema hinaus – sie stimulierten viele Ideen und Entwicklungen in der Theorie allgemeiner Differentialgleichungen und der Funktionalanalysis. Außerdem treten Sturm-Lioville Probleme oft auf, z.B. kann die zeitabhängig Schrödingergleichung der Quantenmechanik für ein Teilchen in einem kugelsymmetrischen Potential in dieser Form geschrieben werden. Auch den Grundton einer Trommel erhalt man als Eigenwert eines Sturm-Liouville Problems.

Trotz der weitreichenden Anwendungen ist die Sturm-Liouville Theorie recht elementar verständlich und man kann an dieser Beispielklasse viele Konzepte direkt verstehen und nachrechnen, die in weitergehenden Vorlesungen (auf weit abstrakterem Level) wieder auftauchen werden.

Literatur:

1.)

Titchmarsh – Eigenfunction expansion, Oxford: Clarendon Press, 2nd edition, 1962.

Inhalt:

The study of quadratic forms was historically motivated by number-theoretic questions, such as determining which integers are sums of three squares. But it is also relevant in many a priori unrelated branches of mathematics: it is for example a fundamental tool in the classification of four-manifolds in differential topology.

The goal of the seminar will be the classification of quadratic forms over the field of rational numbers (Hasse-Minkowski theorem) and over the ring of integers. Beside the importance of the results and the method of the proof which is a paradigmatic example of the so-called local-global principle, it will be an opportunity to introduce many tools which are fundamental in modern Number Theory.

If you are interested in giving a talk in the proseminar, please contact me before the end of January at yohan.brunebarbe@math.uzh.ch.

Literatur:

1.)

J.-P. Serre. A course in arithmetic. Graduate Texts in Mathematics 7. Springer-Verlag, 1973

Inhalt:
Paul Erd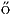s sprach gerne über das Buch, in welchem Gott die perfekten Beweise mathematischer Sätze bewahrt. Martin Aigner und Günter Ziegler verfassten ein Buch mit dem Titel “Proofs from The Book”, das eine Annäherung an das sagenhafte Buch sein soll und Beweise aus der Zahlentheorie, der Geometrie, der Kombinatorik, der Analysis und der Graphentheorie enthält. (Ursprünglich war Erd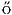s als Mitverfasser beteiligt, doch er verstarb 1996.) Im Proseminar werden wir das Geometrie-Kapitel aus “Proofs from The Book” studieren. Mögliche Themen hieraus sind unter anderem: Das dritte Hilbert’sche Problem, Zerlegungen von Polyedern und Graphen, die Euler’sche Formel, der Cauchy’sche Starrheitssatz, die Borromäischen Ringe, Simplizes und Borsuks Vermutung.

Literatur:

1.)

Martin Aigner, Günter M. Ziegler. Proofs from The Book. Fifth edition. Including illustrations by Karl H. Hofmann. Springer-Verlag, Berlin, 2014

Inhalt:
Die konvexe Analysis untersucht die Eigenschaften von konvexen Mengen und Funktionen mit Methoden der Analysis und Geometrie. Neben Anwendungen in der reinen Mathematik bildet die konvexe Analysis die Grundlage für die sogenannte konvexe Optimierung, welche in einer großen Klasse von Optimierungsproblemen Anwendung findet.

In dem Proseminar erarbeiten wir vor allem die mathematischen Grundlagen der konvexen Analysis. Je nach Interesse befassen wir uns mit den folgenden Themen:

• Eigenschaften konvexer Mengen
• Eigenschaften konvexer Funktionen
• Sublinearität und Subdifferential
• Konjugation
• Dualität

Literatur:

1.)

Jean-Baptiste Hiriart-Urruty, Claude Lemarechal; Fundamentals of Convex Analzsis, (Springer, 2001)

Inhalt:
Das Seminar richtet sich an Studierende, die eine Bachelorarbeit im Bereich Geometrische Analysis schreiben wollen, sowie an Studierende im Master.

Ein Teil der Vorträge wird direkt an die Vorlesung über Partielle Differentialgleichungen im WS 2017/2018 anknüpfen. Themen sind elliptische Systeme auf Vektorbündeln und Parabolische Gleichungen bzw. Systeme.

In einem zweiten Teil der Vorträge werden ausgewählte Themen zur geometrischen Analysis von Flächen behandelt. Dazu sind Vorkenntnisse aus der Differentialgeometrie von Flächen nützlich.

Die Gewichtung der beiden Teile wird von der Hörerschaft abhängig gemacht werden.

Literatur wird in der Vorbesprechung bekannt gegeben._____________________________________________

Inhalt:
 
Wir kennen Galoisgruppen als wesentliche Invariante von Körpererweiterungen. Galoiskohomologie ist eine systematische Methode zum Studium von Galoisgruppen und ihrer Wirkung auf natürlichen Objekten wie der additiven oder multiplikativen Gruppe eines Körpers. Ein besonders interessantes Beispiel ist die Klassifikation aller Erweiterungen mit zyklischer Galoisgruppe, bekannt als Kummertheorie und (in positiver Charakteristik) Artin-Schreier-Theorie.

Wir werden uns sowohl mit der allgemeinen Theorie, also auch diesen und anderen konkreten Anwendungen beschäftigen.

Literatur:

1.)

S. Bosch: Algebra, Springer Verlag.

2.)

J.-P. Serre, Local Fields, Springer Verlag.

Inhalt:
Wir betrachten Untermannigfaltigkeiten von Riemannschen Mannigfaltigkeiten. Dabei beginnen wir mit grundlegenden Fragen und zeigen die Sätze von Gauß und Codazzi-Mainardi. Anschließend folgen Einzelvorträge und kleinere Blöcke zu einigen der folgenden Themen (weitere Themen auf Anfrage). Die Auswahl erfolgt bei der Vorbesprechung.

Minimalflächen. Wir betrachten die erste und zweite Variationsformel für das Volumen. Aus der ersten Variationsformel erhalten wir den Begriff einer minimalen Untermannigfaltigkeit. Die zweite Variationsformel sagt etwas über ihre Stabilität aus.

Kalibrierungen. Bestimmte Differentialformen erlauben es, die Minimalität einer Untermannigfaltigkeit einfach nachzuweisen. Dieses Phänomen tritt beispielsweise in Kähler-Mannigfaltigkeiten auf.

Hindernisse gegen positive Skalarkrümmung. Minimale Hyperflächen von Mannigfaltigkeiten mit positiver Skalarkrümmung tragen wieder Metriken mit positiver Skalarkrümmung. Schoen und Yau haben auf diese Weise ein Hindernis gegen positive Skalarkrümmung gefunden.

Vergleichssätze für Skalarkrümmung. Mit ähnlichen Methoden wie Schoen und Yau geben Gromov und Lawson Vergleichssätze für Untermannigfaltigkeiten in Mannigfaltigkeiten mit einer unteren Schranke an die Skalarkrümmung.

Literatur: wird noch bekanntgegeben.__________________________________________________________________

Inhalt:
The concept of a Lie group arises naturally by putting together the algebraic notion of a group with the geometric notion of a smooth manifold. A Lie group is a smooth manifold with a group structure such that the group operations are smooth. Lie groups arise in a natural way as symmetries of a geometric object. The general linear group GL_n(ℝ) is our guiding example of a Lie group. A representation of a Lie group G on a vector space V is a group homomorphism ρ: G → GL(V ). Similarly, the notion of Lie algebra appears naturally. For example, the tangent space 𝔤 at the identity element of a Lie group G has this structure. For G = GL_n(ℝ), this yields 𝔤 = Mat_ℝ(n × n) with the composition rule given by the commutator [X,Y ] = XY - Y X. A vector space with such a composition rule is called a Lie algebra.

In this seminar, we will study (matrix) Lie groups, Lie algebras and their representations. We will introduce the notion of Lie groups and Lie algebras and discuss the correspondence between them. Since finite dimensional “semisimple” Lie algebras can be viewed as elementary building blocks of more complicated Lie algebras, we will study them with an emphasis on the structure theory and their representations. Finally, we will discuss representations of Lie groups and prove a version of the Peter-Weyl Theorem, which is a statement about using irreducible representations of a compact Lie group G to study the Hilbert space of square integrable functions on G with respect to the so-called Haar measure. As a corollary of the Peter-Weyl theorem, it follows that every compact Lie group can be realized as a matrix Lie group.

Literatur:

1.)

T. Bröcker, T. Dieck, Representations of Compact Lie Groups, Springer-Verlag, 2003, Chapters I–III

2.)

J. E. Humphreys, Introduction to Lie Algebras and Representation Theory, Springer-Verlag, 1974

3.)

A. Knapp, Lie groups Beyond an Introduction, Birkhäuser, 2002, Chapters I–V

Inhalt:
der Mächtigkeit κ isomorph sind. Der Satz von Morley besagt, dass eine κ-kategorische Theorie in einer abzählbaren Sprache, für κ > ℵ₀, ist dann λ-kategorisch für alle λ > ℵ₀. Der Satz von Morley folgt aus dem Satz von Baldwin-Lachlan, welcher besagt, dass eine abzählbare Theorie ohne endliche Modelle ist genau dann überabzählbar kategorisch, wenn sie ω-stabil ist und keine Vaughtschen Paare besitzt. Die Ideen und Methoden, welche im Beweis des Satzes von Baldwin-Lachlan vorkommen, sind zum Kern der Stabilitätstheorie und der sogenannten geometrischen Modelltheorie, welche viele Verknüpfungspunkte mit anderen Gebieten der reinen Mathematik besitzt, z. B. Algebraische Geometrie, Zahlen- oder Körpertheorie.

Im Seminar werden wir etliche Eigenschaften ω-stabiler Theorien lernen, insbesondere streng minimaler Theorien. Klassische Begriffe der Stabilitätstheorie, unter anderen Erbe/Koerbe, definierbare Typen, Morley Rang und Folgen, usw. werden eingeführt und studiert. Mit Hilfe des Morleyranges werden wir den Sazt von Macintyre beweisen, welcher besagt, dass ein ω-stabiler unendlicher Körper algebraisch abgeschlossen ist.

Literatur:

1.)

K. Tent & M. Ziegler : A Course in Model Theory, (2012), Cambridge University Press.

2.)

A. Pillay : An Introduction to Stability Theory, (2008), Dover Books on Mathematics.

3.)

A. Poizat : Stable Groups, (2001), Mathematical Surveys & Monographs

Inhalt:
Viele Phänomene in der Natur lassen sich durch mathematische Modelle, insbesondere durch partielle Differentialgleichungen, beschreiben. Die wichtigsten unter diesen sind die elliptischen, die parabolischen und die hyperbolischen Differentialgleichungen. Gesucht werden jeweils Funktionen mehrerer Veränderlicher, deren Ableitungen gewisse Gleichungen erfüllen. Eine besondere Klasse von partiellen Differentialgleichungen bilden die hyperbolischen Erhaltungssätze. Trotz beliebig glatter Daten (damit sind Randwerte, Anfangswerte und die Koeffizienten gemeint), können die zugehörigen Lösungen unstetig sein. Daher ist ihre Behandlung eine besondere Herausforderung an die Analysis und die Numerik. Diese Differentialgleichungen sind mathematische Modelle für Strömungen kompressibler Gase und für verschiedene Probleme aus den Bereichen Astrophysik, Grundwasserströmungen, Meteorologie, Halbleitertechnik und reaktive Strömungen. Es ist das Ziel des Seminars, die theoretischen Grundlagen wie Existenz und Eindeutigkeit von Lösungen, zu zeigen und die Entwicklung und Analyse von numerischen Algorithmen.

Literatur:

1.)

M. Feistauer, J. Felcman, I. Straskraba, Mathematical and computational methods for compressible flow, Oxford Science Publications 2003.

2.)

D. Kröner, Numerical schemes for conservation laws, Wiley und Teubner 1997.

3.)

R. LeVeque, Numerical methods for conservation laws, Birkhäuser Verlag 1992.

Inhalt:
Im Seminar sollen weiterführende Themen der numerischen Behandlung partieller Differentialgleichungen mit Nebenbedingungen oder kritischen Parametern behandelt werden. Beispiele dafür sind die iterative Lösung diskreter Sattelpunktprobleme, die Analyse sogenannter virtueller Finite-Elemente-Methoden sowie Anwendungen im Elektromagnetismus.

Literatur:

1.)

S. Bartels: Numerical Approximation of Partial Differential Equations. Springer, 2016.

2.)

D. Braess: Finite Elemente. Springer, 2007.

3.)

D. Boffi, F. Brezzi, M. Fortin: Mixed Finite Element Methods and Applications. Springer, 2013.

4.)

M. Dobrowolski: Angewandte Funktionalanalysis. Springer, 2005.

5.)

P. Knabner, L. Angermann: Numerical Methods for Elliptic and Parabolic PDEs. Springer, 2000.

6.)

C. Grossmann, H.-G. Roos: Numerische Behandlung partieller Differentialgleichungen. Springer, 2005.

Inhalt:

Finding structure in diversity between humans has long interested researchers. Most scientific inquirires are based on (oftentimes implicite) conceptual assumptions about the basic units of that structure: race, population or gradient. Since the availability of DNA as inherited character, these differences have become a new and highly quantifiable aspect. However, at the same time, choosing and demarcating human groups and individuals to represent certain populations, races or gradients entails many non-quantitative decisions and processes. Similarly, choosing methods, models, and markers also entails choices that are not always obvious or without alternatives.

This seminar is a cross-disciplinary teaching project with the Bachelor of Arts and Sciences and Mathematics as key players. We will discuss statistical methods from the field of (human) population genetics and, on that basis, also consider the validity of the research results. Furthermore, we will examine the societal assumptions about (and imaginations of) human societies that inform the research designs of these studies. We will discuss possible consequences of that research field in epistemological and societal perspective. To do so, we will work exemplarily with a few populations covered by human population genetic studies.

The specific goal of this seminar is to learn with and from each other about the many facets (methodological, societal, political, biological, anthropological, etc.) of a seemingly homogeneous research topic.__________________________________________________________________________________________________

Inhalt:

Glücksspiele haben bekanntlich bereits in der früher Geschichte der Stochastik eine große Rolle gespielt. Doch auch in der modernen Theorie der Wahrscheindlichkeitstheorie können (faire) Glücksspiele als Motivation des Begriffs Martingal gesehen werden. In diesem Seminar werden sowohl Grundlagen (Bedingte Erwartungen, Markov-Ketten, Martingale) als auch Anwednungen (Roulette, Poker, etc) besprochen.

Dieses Seminar ist ausdrücklich für Lehramtskandidaten geeignet.

Literatur:

1.)

S. N. Ethier. The Doctrine of Chances. Springer, 2010.

2.)

L. E. Dubbins, L. J. Savage. Inequalities for Stochastic Processes. How to Gamble if You Must. McGraw–Hill., 1965

Inhalt:

Aufbauend auf der Vorlesung Wahrscheinlichkeitstheorie werden in dieser Veranstaltungen Themen für eine erste Abschlussarbeit in Mathematik (Bachelor oder Zulassungsarbeit) vorgestellt. Die Themen können sowohl direkt an die Vorlesung Wahrscheinlichkeitstheorie anschließen, als auch Anwendungen enthalten, z.B. aus den Themenbereichen Finanzmathematik, Statistik oder Biologie.__________________________________________________________________________________________________________

Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik dienen.

Vorbesprechung mit Hinweisen auf einführende Literatur:
Mi, 31.01.2018, 10:30–11:30 Uhr, Konferenzraum Institut für Medizinische Biometrie und Statistik, Stefan-Meier-Str. 26, 1. OG

Vorherige Anmeldung per E-Mail (sec@imbi.uni-freiburg.de) ist erwünscht._____________

Inhalt:
 
Das Seminar beschäftigt sich mit topologischen Räumen kleiner Dimension, also Kurven, Flächen und 3-Mannigfaltigkeiten. Unser Ziel ist es, diese Mannigfaltigkeiten kennenzulernen, zu untersuchen und – soweit möglich – eine Klassifikation zu erreichen. Die Betonung wird auf Invarianten der niedrigdiemansionalen Mannigfaltigkeiten. Das Seminar bietet eine Einführung in dieses attraktive und aktive Forschungsgebiet.

Das Seminar richtet sich an Studenten der Mathematik oder Physik ab dem 5. Semester und kann insbesondere der Vorbereitung einer Bachelorarbeit (oder auch Masterarbeit) dienen.

Literatur:

1.)

Milnor. Topology from the Differentiable Viewpoint.

2.)

Donaldson. Riemann Surfaces.

3.)

Saveliev. Lectures on the topology of 3-manifolds.

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann.

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe (einem Oberseminar, Projektseminar …)) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im Vertiefungsmodul gibt es eine mündliche Abschlussprüfung über den Stoff des Lesekurses und den weiteren Stoff des Moduls.____________________________________________

Inhalt:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology or mathematical physics or a mix thereof.

The precise topic will be chosen at the end of the preceeding semester. The program will be made available via our web site.

The level is aimed at our doctoral students. Master students are very welcome to participate as well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. A. Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________

Inhalt:
The Joint Seminar is a research seminar in complex and algebraic geometry, organized by the research groups in Freiburg, Nancy and Strasbourg. The seminar meets roughly twice per semester in Strasbourg, for a full day. There are about four talks per meeting, both by invited guests and by speakers from the organizing universities. We aim to leave ample room for discussions and for a friendly chat.

The talks are open for everyone. Contact one of the organizers if you are interested in attending the meeting. We have some (very limited) funds that might help to support travel for some junior participants.____________________________________________________________________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17:00 Uhr im Hörsaal II in der Albertstr. 23 b statt.

Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Eckerstraße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/