Lehrveranstaltungen

Inhalt:
 
Diese Vorlesung ist die Fortsetzung der 2-stündigen Vorlesung Stochastik aus dem WS 2013/14. Sie ist eine Einführung in die Wahrscheinlichkeitsrechnung und Statistik ohne Maßtheorie. In dieser Veranstaltung werden die Denk- und Schlussweisen, die für die mathematische Behandlung von Zufallserscheinungen typisch sind, entwickelt. In diesem Semester werden Themen wie Kombinatorik bei Random Walks, Markov-Ketten und Grundtatsachen der Statistik behandelt werden.

Die Vorlesung ist zweisemestrig und richtet sich an Bachelor- und Lehramtsstudenten.
Der Stoff der Vorlesung kann als Prüfungsstoff für Staatsexamensprüfungen verwendet werden.
Der Besuch der Übungen und der Praktischen Übung wird dringend empfohlen.

Literatur:

1.)

Dümbgen, L.: Stochastik für Informatiker, Springer 2003

2.)

Georgi, H.-O.: Stochastik, Walter de Gruyter 2002

3.)

Kersting, G.; Wakolbinger, A.: Elementare Stochastik, Birkhäuser 2008

4.)

Krengel, U.: Einführung in die Wahrscheinlichkeitstheorie und Statistik, Vieweg 2005

Inhalt:
Die Numerik ist eine Teildisziplin der Mathematik, die sich mit der praktischen Lösung mathematischer Aufgaben beschäftigt. Dabei werden Probleme in der Regel nicht exakt sondern approximativ gelöst. Typische Beispiele sind die Bestimmung von Nullstellen einer Funktion oder die Lösung linearer Gleichungssysteme. In der Vorlesung werden einige grundlegende numerische Algorithmen vorgestellt und im Hinblick auf Rechenaufwand sowie Genauigkeit untersucht. Die Vorlesung ist der zweite Teil eines zweisemestrigen Kurses. Der Besuch der begleitenden praktischen Übungen wird empfohlen. Diese finden 14-täglich im Wechsel mit der Übung zur Vorlesung statt.

Literatur:

1.)

R. Plato: Numerische Mathematik kompakt. Vieweg, 2006

2.)

R. Schaback, H. Wendland: Numerische Mathematik. Springer, 2004.

3.)

J. Stoer, R. Bulirsch: Numerische Mathematik I, II. Springer, 2007, 2005.

4.)

M. Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Vieweg+Teubner, 2006.

Inhalt:
Wir betrachten eine axiomatische Charakterisierung der affinen, Euklidischen und projektiven Geometrie. Ein anderes wichtiges Beispiel wird die hyperbolische Geometrie liefern, die bis auf das Parallelenaxiom alle Axiome der Euklidischen Geometrie erfüllt. Nach weiterführenden geometrischen Konstruktionen beweisen wir auch ein topologisches Resultat, die Eulersche Polyederformel.

Diese Vorlesung richtet sich hauptsächlich an Lehramtsstudenten/innen und ist Pflichtveranstaltung für alle Studierende im Lehramt mit Haupt- und Beifach Mathematik, die nach der neuen Prüfungsordnung (gültig ab WS 2010/11) geprüft werden.

Literatur:

1.)

C. Bär, Elementare Differentialgeometrie, Walter de Gruyter, 2010.

2.)

N. Efimov, Über die Grundlagen der Geometrie. Höhere Geometrie. Bd. I, Vieweg, 1970.

3.)

R. Hartshorne, Geometry: Euclid and beyond, Springer, 2000.

4.)

H. Knörrer, Geometrie, Vieweg, 1996.

Inhalt:
Die Funktionentheorie befasst sich mit Funktionen in einer komplexen Veränderlichen. Sie ist ein schönes und interessantes Teilgebiet der Mathematik, das sowohl in vielen Bereichen der Mathematik als auch beispielsweise in der Physik Anwendungen hat.

Komplex differenzierbare Funktionen f: U → ℂ auf einem Gebiet U ⊂ ℂ nennt man holomorph. Eine holomorphe Funktion erfüllt die Cauchy-Riemann-Differentialgleichungen und hat daher viele schöne Eigenschaften. Zum Beispiel ist jede holomorphe Funktion analytisch, das heißt, sie ist unendlich oft differenzierbar und wird lokal stets durch ihre Taylorreihe dargestellt. Eine holomorphe Funktion auf der abgeschlossenen Kreissscheibe wird bereits durch ihre Werte auf dem Rand vollständig bestimmt.

Wir lernen zunächst die Grundlagen der Funktionentheorie kennen wie den Cauchyschen Integralsatz, die Cauchysche Integralformel, das Maximumprinzip, den Satz von Liouville und den Residuensatz. Anschließend beschäftigen wir uns mit dem Riemannschen Abbildungssatz, und, sofern die Zeit es erlaubt, mit weiteren Themen.

Literatur:

1.)

Jänich, Klaus, Funktionentheorie, Springer-Verlag, Berlin, 1993

Weitere Literatur wird in der Vorlesung angegeben.__________________________________________________________

Inhalt:
Im Zentrum dieser Vorlesung steht der Begriff der Stetigkeit. Im ersten Teil, der sogenannten mengentheoretischen Topologie, wird ein sehr allgemeiner begrifflicher Rahmen für das Studium dieses Begriffs bereitgestellt, der für viele weitere Vorlesungen von der Funktionalanalysis über die Differentialgeometrie bis zur Zahlentheorie grundlegend ist.

Im zweiten Teil geht es um die Fundamentalgruppe und eine Einführung in die algebraische Topologie. Wir wollen zum Beispiel zeigen, daß es keine stetige injektive Abbildung von der Kugelschale in die Ebene gibt, daß sich ein Igel nicht wirbelfrei kämmen läßt, und daß ein mehrfach um den Ursprung laufender geschlossener Weg nicht injektiv sein kann.

Literatur:

1.)

M.A. Armstrong, Basic Topologie, Springer 1983

2.)

K. Jänich, Topologie, Springer 2001

3.)

E. Ossa, Topologie, Vieweg + Teubner 2009

4.)

W. Soergel, Skriptum Topologie

Inhalt:
Es handelt sich um eine Grundvorlesung im algebraischen Bereich. Vorausgesetzt wird lineare Algebra, hilfreich ist der Stoff der Vorlesung Algebra und Zahlentheorie. Andererseits wird bei den weiterführenden Veranstaltungen zu algebraischen Themen (algebraische Geometrie, Zahlentheorie, Darstellungstheorie, …) der Inhalt der kommutativen Algebra (also dieser Vorlesung) vorausgesetzt werden. Es besteht die Möglichkeit eine Bachelor-Arbeit im Bereich algebraische Geometrie aufbauend der Vorlesung anzufertigen.

Zum Inhalt: Kommutative Algebra ist eine allgemeinere Version der linearen Algebra über kommutativen Ringen statt über Körpern. Der Begriff des Moduls ersetzt den des Vektorraums. Auch weite Teile von Geometrie und Analysis verwenden diese Konzepte oder Variationen. Hauptanwendungsgebiet sind jedoch Zahlentheorie und algebraische Geometrie. Wir werden die formale Theorie daher mit einem der wichtigsten Anwendungsfälle kombinieren und gleichzeitig die Grundlagen der algebraischen Geometrie erarbeiten.

Algebraische Varietäten sind Teilmengen von kⁿ (dabei k ein zunächst algebraisch abgeschlossener Körper), die durch Polynomgleichungen mit Koeffizienten in k definiert werden. Dies sind geometrische Objekte, für k = C sogar analytische. Wir studieren sie mit algebraischen Methoden. Die Theorie der affinen Varietäten entspricht der Theorie der Ideale in Polynomringen mit endlich vielen Variablen. Damit ist der Bogen zur kommutativen Algebra gespannt. Ziel der Veranstaltung ist der Beweis (einer Verallgemeinerung) des Satzes von Bézout zum Schnittverhalten von algebraischen Varietäten.

Literatur:

1.)

Eisenbud, Commutative Algebra with a view towards algebraic geometry

2.)

Atiyah, MacDonald, Introduction to Commutative Algebra

3.)

Shafarevich, Basic algebraic geometry

Inhalt:
Die lineare Funktionalanalysis, um die es in der Vorlesung geht, verwendet Konzepte der linearen Algebra wie Vektorraum, linearer Operator, Dualraum, Skalarprodukt, adjungierte Abbildung, Eigenwert, Spektrum, um Gleichungen in unendlichdimensionalen Funktionenräumen zu lösen, vor allem lineare Differentialgleichungen. Die algebraischen Begriffe müssen dazu durch topologische Konzepte wie Konvergenz, Vollständigkeit, Kompaktheit erweitert werden. Dieser Ansatz ist erst zu Beginn des 20. Jahrhunderts u.a. von Hilbert entwickelt worden, er gehört aber nun zum methodischen Fundament der Analysis, der Numerik sowie der Mathematischen Physik, insbesondere der Quantenmechanik, und ist auch in anderen mathematischen Gebieten unverzichtbar.

Ein Schwerpunkt wird auf den Aspekten liegen, die für partielle Differentialgleichungen relevant sind.

Literatur:

1.)

Alt, H.W.: Lineare Funktionalanalysis (4. Auflage), Springer 2002.

2.)

Bachmann, G. & Narici, L.: Functional Analysis, Academic Press 1966.

3.)

Brézis, H.: Analyse Fonctionelle, Masson, Paris 1983.

Inhalt:

Das Ziel der Variationsrechnung ist, gewisse mathematisch fassbare Größen zu minimieren oder zu maximieren. Genauer gesagt betrachten wir auf Ω ⊂ ℝⁿ Funktionale bzw. Variationsintegrale der Form

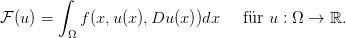
Beispiele sind Bogenlänge und Flächeninhalt, sowie Energien von Feldern in der Physik. Die zentrale Fragestellung ist die Existenz von Minimierern. Nach einer kurzen Vorstellung der funktionalanalytischen Hilfsmittel, werden wir zunächst einige notwendige und hinreichende Bedingungen für die Existenz von Minimierer kennenlernen. Wir werden sehen, dass Kompaktheit dabei eine ausgesprochen wichtige Rolle spielt. Anschließend werden wir einige Techniken vorstellen, die uns in Spezialfälle hilft, auch ohne Kompaktheit auszukommen: Die sogenannte kompensierte Kompaktheit und die konzentrierte Kompaktheit.

Literatur:

1.)

M. Struwe, Variational methods. Applications to nonlinear partial differential equations and Hamiltonian systems Fourth edition. A Series of Modern Surveys in Mathematics], 34. Springer-Verlag, Berlin, 2008.

2.)

J.Jost, X.Li-Jost, Calculus of Variations, Cambridge Univ.Press, 1999

Inhalt:
Zahlentheorie beschäftigt sich mit den Eigenschaften der ganzen Zahlen. Fragen nach der Lösbarkeit von Gleichungen (z.B. x³ + y³ = z³) führen schnell dazu, dass man den Zahlbereich vergrößert (zB. x³ + y³ = (x + y)(x + ρy)(x + ρ²y) für ρ = e^2πi∕3). Algebraische Zahlentheorie konzentriert sich auf diese Verallgemeinerungen von Z und ihre Eigenschaften.

Wir wollen diese Zahlbereiche definieren und ihre grundlegenden Eigenschaften studieren. Wichtigste Ziele sind die Endlichkeit der Klassenzahl (sie misst, wie sehr die Eindeutigkeit der Primfaktorzerlegung fehlschlägt) und der Dirichletsche Einheitensatz.

Literatur:

1.)

S. Lang, Algebraic Number Theory

2.)

J. Neukirch, Algebraic Number Theory

3.)

P. Samuel, Algebraic Theory of Numbers

4.)

A. Schmidt, Einführung in die algebraische Zahlentheorie

Inhalt:
Die Komplexe Geometrie verbindet zwei Gebiete in der Mathematik: Die Differentialgeometrie und die algebraische Geometrie. Sie kann als ein Spezialfall der klassischen Riemannschen Geometrie verstanden werden, in dem wesentliche neue Techniken zur Verfügung stehen, nämlich die der komplexen Funktionentheorie. Dies erlaubt interessante Anwendungen, z.B. im Zusammenhang mit sogenannten Calabi-Yau Mannigfaltigkeiten, die in der modernen theoretischen Physik eine wesentliche Rolle spielen.

Ziel der Vorlesung ist es, die wichtigsten und grundlegenden Techniken zum Studium solcher komplexer Mannigfaltigkeiten zu lehren und einige Beispielklassen sowie Anwendungen zu diskutieren. Insbesondere werden wir sogenannte Kählermannigfaltigkeiten und ihre besonderen Eigenschaften studieren, d.h. Mannigfaltigkeiten, deren Riemannsche Metrik eng mit der komplexen Struktur verworben ist. Die für die theoretische Physik relevanten Beispielklassen werden ausführlich behandelt, nämlich die erwähnten Calabi-Yau Mannigfaltigkeiten, und unter diesen insbesondere die K3-Flächen. Weiter sollen Techniken aus der theoretischen Physik eingeführt werden, wie etwa die Konstruktion von Vertexalgebren aus geeigneten geometrischen Daten. Wie wir sehen werden, erlauben die Vertexalgebren den Brückenschlag zwischen Geometrie und Quantenfeldtheorie.

Es werden Grundkenntnisse aus der Differentialgeometrie sowie Funktionentheorie vorausgesetzt; aus der theoretischen Physik, der Quantenfeldtheorie und aus der algebraischen Geometrie wird kein Vorwissen vorausgesetzt.

Literatur:

1.)

D. Huybrechts, Complex Geometry, Springer 2005

2.)

R.O. Wells, Differential Analysis on Complex Manifolds, Springer 1986

3.)

W.P. Barth, K. Hulek, Ch.A.M. Peters, A. van de Ven, Compact Complex Surfaces, Springer 2004, Kapitel VIII

4.)

I. Frenkel, D. Ben-Zvi, Vertex algebras and algebraic curves, Mathematical Surveys and Monographs 88, AMS, Providence, RI (2004), Kapitel 1-4

Inhalt:
Die Veranstaltung schließt an die Vorlesung Stochastische Prozesse aus dem WS 2013/14 an. Ein zentrales Thema sind stochastische Integrale eines adaptierten Prozesses bezüglich einer Brownschen Bewegung und bezüglich allgemeineren Klassen stochastischer Prozesse.

Darauf aufbauend werden die Itô-Formel und stochastische Differentialgleichungen behandelt. Als Anwendung wird eine Einführung in die Finanzmathematik gegeben, wobei die Black-Scholes-Theorie für Optionsbewertung im Zentrum stehen wird.

Literatur:

1.)

O. Kallenberg: Foundations of Modern Probability, Springer 2002

2.)

A. Klenke: Wahrscheinlichkeitstheorie, Springer 2008

3.)

D. Lamberton, B. Laperyre: Introduction to Stochastic Calculus Applied to Finance. Chapman and Hall 2002

4.)

P. Protter: Stochastic Integration and Differential Equations, Springer 2003

5.)

S. Shreve: Stochastic Calculus for Finance II: Continuous-Time Models, Springer 2008

Inhalt:
Viele Phänomene in der Natur lassen sich durch mathematische Modelle, insbesondere durch partielle Differentialgleichungen, beschreiben. Die wichtigsten unter diesen sind die elliptischen, die parabolischen und die hyperbolischen Differentialgleichungen. Gesucht werden jeweils Funktionen mehrerer Veränderlicher, deren Ableitungen gewisse Gleichungen erfüllen.

Eine besondere Klasse von partiellen Differentialgleichungen bilden die hyperbolischen Erhaltungssätze. Trotz beliebig glatter Daten (damit sind Randwerte, Anfangswerte und die Koeffizienten gemeint), können die zugehörigen Lösungen unstetig sein. Daher ist ihre Behandlung eine besondere Herausforderung an die Analysis und die Numerik.

Diese Differentialgleichungen sind z. B. mathematische Modelle für Strömungen kompressibler Gase und für verschiedene Probleme aus den Bereichen Astrophysik, Grundwasserströmungen, Meteorologie, Halbleitertechnik und reaktive Strömungen. Beispielsweise ist das mathematische Modell für eine Supernova von derselben Struktur wie das für die Verbrennung in einem Fahrzeugmotor. Kenntnisse in diesen Bereichen werden aber nicht vorausgesetzt. In der Vorlesung sollen die Grundlagen geschaffen werden, um Simulationen der oben genannten Probleme am Computer durchzuführen.

Die Vorlesung setzt die Veranstaltung „Theorie und Numerik partieller Differentialgleichungen I“ aus dem Wintersemester 2012/13 fort. Kenntnisse in Theorie oder Numerik für elliptische oder parabolische Differentialgleichungen werden nicht vorausgesetzt. Parallel zur Vorlesung findet ein numerisches Praktikum statt.

Literatur:

1.)

D. Kröner, Numerical Schemes for Conservation Laws, Wiley und Teubner, Chichester, Stuttgart (1997).

2.)

R. J. LeVeque, Numerical methods for Conservation Laws, Birkhäuser Verlag, Basel, (1992).

3.)

R. J. LeVeque, Finite Volume Methods for Hypberbolic Problems, Cambridge Texts in Applied Mathematics (2002).

4.)

G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter, Berlin, New York (2010).

Inhalt:
Die Vorlesung Mathematische Logik ist die erste Vorlesung eines Logikzyklus. Sie besteht aus vier Teilen:

1.

Der Prädikatenkalkül
Der Gödelsche Vollständigkeitssatz zeigt, wie sich logisches Schließen formalisieren läßt.

2.

Mengenlehre
Das Axiomensystem der Mengenlehre wird eingeführt. Die gesamte Mathematik folgt (wenn man will) formal–logisch aus diesen Axiomen.

3.

Rekursionstheorie
Der Begriff der Berechenbarkeit wird streng gefaßt. Eigentliches Ziel ist es aber, den rekursionstheoretischen Gehalt des Prädikatenkalküls zu verstehen.

4.

Arithmetik
Die Arithmetik ist ein Teilsystem der Mengenlehre, das groß genug ist, Prädikatenkalkül und Rekursionstheorie zu formalisieren. Es ergeben sich die paradoxen Gödelschen Unvollständigkeitssätze.

Literatur:

1.)

Ziegler Mathematische Logik, Birkhäuser, 2010

2.)

Shoenfield Mathematical Logic

Inhalt:
Der Begriff von Gamma-Konvergenz wird eingeführt und Anwendungen im Rahmen der Geometrischen Analysis und der Theorie der Phasenübergänge werden gezeigt. Weitere Anwendungen, je nach Interesse der Teilnehmer, können angesprochen werden.

Literatur:

1.)

Dal Maso, G.: An Introduction to Γ-Convergence, Birkhäuser Boston, 1993.

2.)

Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs, The Clarendon Press, Oxford UP, New York, 2000.

Inhalt:
Mit dem Begriff Statistisches Lernen werden verschiedene statistische Methoden bezeichnet, die dabei helfen, komplexe Datensätze zu modellieren und zu verstehen. Diese Methoden lernen aus den vorhandenen Daten und ziehen Schlussfolgerungen für die Modellierung der Grundgesamtheit. Statistische Lernverfahren werden oft auch den Begriffen Data-Mining oder Machinelles Lernen zugeordnet. Statistisches Lernen findet heute in sehr vielen Bereichen Anwendung, beispielsweise in der medizinisch/biologischen Forschung oder bei der Analyse von Kundendaten.

Die Vorlesung gibt eine einführende Übersicht in die Theorie des statistischen Lernens und ihre praktische Anwendung. In der Vorlesung werden zunächst die grundlegenden Prinzipien erarbeitet. Danach werden einzelne Methoden näher beleuchtet. In den Übungen werden die Kenntnisse sowohl theoretisch als auch praktisch vertieft. Der praktische Teil der Übungen basiert auf frei zugänglichen R-Datensätzen, z. B. aus den Lebenswissenschaften.

Literatur:

1.)

T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer, 2001

2.)

S. Kulkarni, G. Harman, An Elementary Introduction to Statistical Learning Theory, J. Wiley, 2011

3.)

V. N. Vapnik, Statistical Learning Theory, J. Wiley, 1996

4.)

B. Clarke, E. Fokoue, H. H. Zhang, Principles and Theory for Data Mining and Machine Learning, Springer, 2009

Inhalt:

Viele Probleme aus Naturwissenschaft und Technik, wie etwa die zeitliche Änderung der Temperatur in einem Raum, lassen sich durch partielle Differentialgleichungen modellieren. Häufig ist man daran interessiert, durch Steuerung äußerer Einflüsse, wie z. B. die Positionierung eines Heizkörpers, eine „optimale“ Konfiguration zu erreichen. Neben der eigentlichen Lösung soll dann auch die Steuerung bestimmt werden, die zur Minimierung der „Kosten“, im Beispiel etwa der Energiezufuhr, führt. Mathematisch spricht man von Optimalsteuerungsproblemen für partielle Differentialgleichungen.

Inhalt dieser Vorlesung ist eine Einführung in die Theorie und Numerik von Optimalsteuerungsproblemen für elliptische und parabolische partielle Differentialgleichungen. Begleitend zur Vorlesung werden wöchentliche Übungen angeboten.

Literatur:

1.)

M. Hinze et al., Optimization with PDE constraints, Springer, 2009

2.)

F. Tröltzsch, Optimale Steuerung partieller Differentialgleichungen, Vieweg+Teubner, 2009

Inhalt:
Credit risk represents by far the biggest risk in the activities of a traditional bank. In particular, during recession periods financial institutions loose enormous amounts of money as a consequence of bad loans and default events. In the last two decades, a multitude of credit-linked derivatives has been developed to manage and transfer credit risks in an efficient and standardized way. These allow banks to shape their risk profile according to regulatory standards.

In this lecture, we introduce some of the most popular single name- and portfolio credit models and show how these are used to measure credit risk and to price credit derivatives like credit default swaps (CDS), basket default swaps and defaultable bonds. We will also discuss concentration risks in credit portfolios and granularity adjustments.

The course, which is taught in English, is offered for students in the Finance profile of the M.Sc. Economics, but is also open to other master students in both economics and mathematics.

Literatur:

1.)

Bielecki, T.R., Rutkowski, M.: Credit Risk: Modeling, Valuation, and Hedging. Springer, 2002

2.)

Bluhm, C., Overbeck, L.: Structured credit portfolio analysis, baskets & CDOs. Chapman & Hall/CRC Press, 2006

3.)

Duffie, D., Singleton, K.F.: Credit Risk: Pricing, Measurement, and Management. Princeton University Press, 2003

4.)

Lando, D.: Credit Risk Modeling: Theory and Applications. Princeton University Press, 2004

5.)

Lütkebohmert, E.: Concentration Risk in Credit Portfolios. Springer, 2009

6.)

Schönbucher, P.J.: Credit Derivatives Pricing Models. Wiley, 2003

Inhalt:
Within the elementary arbitrage pricing theory, interest rates are usually assumed to be constant. However, this assumption is, of course, not very realistic. In fact, the variation of interest rates is one of the major risks financial institutions like banks and insurance companies are exposed to. To manage and control these risks, there exists a large variety of interest-linked products and derivatives, and the amount of money invested in interest rate markets typically is much higher than in stock markets.

In this lecture, we will introduce the most important interest-based products and related contracts like bonds, swaps, caps/floors, interest rate futures as well as swaptions and show how they can be priced in different interest rate models. We will discuss short rate- as well as forward rate models in this context. Most of these are driven by a Brownian motion, therefore some basic knowledge on this process and related stochastic differential equations would be desirable. If there is some time left at the end, we may also study some market models for LIBOR modeling.

The course, which is taught in English, is offered for students in the Finance profile of the M.Sc. Economics, but is also open to other master students in both economics and mathematics.

Literatur:

1.)

Andersen, L., Piterbarg, V.: Interest rate modeling. Atlantic Financial Press, 2010

2.)

Brigo, D., Mercurio, F.: Interest Rate Models – Theory and Practice (2nd ed.). Springer, 2006

3.)

Filipović, D.: Term-Structure Models: A Graduate Course. Springer, 2009

4.)

Hull, J.C.: Option, Futures, and other Derivatives (7th ed.). Pearson Prentice Hall, 2009

5.)

Zagst, R.: Interest Rate Management. Springer, 2002

Inhalt:
Differentialgleichungen sind ein wichtiges mathematisches Werkzeug zur Beschreibung realer Vorgänge wie beispielsweise der Flugbahn eines Körpers. In der Vorlesung werden numerische Verfahren zur praktischen Lösung gewöhnlicher Differentialgleichungen der Form y′(t) = f(t,y(t)) sowie einfacher partieller Differentialgleichungen, bei denen mehrere unabhängige Variablen auftreten, diskutiert.

Literatur:

1.)

R. Plato: Numerische Mathematik kompakt. Vieweg, 2006

2.)

R. Schaback, H. Wendland: Numerische Mathematik. Springer, 2004.

3.)

J. Stoer, R. Bulirsch: Numerische Mathematik I, II. Springer, 2007, 2005.

4.)

W. Walter: Gewöhnliche Differentialgleichungen: Eine Einführung. Springer, 2000.

5.)

M. Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Vieweg+Teubner, 2006.

Inhalt:
Es werden Aspekte der periodischen Homogenisierung im Bereich der Festkörpermechanik behandelt; (die Theorie hat auch Anwendungen in der Fluidmechanik, z.B. bei Strömungen in porösen Medien ).

Heterogene Materialien und Komposite bestehen aus mehreren Materialien mit z.B. unterschiedlichen elastischen Eigenschaften oder elektrischen Leitfähigkeiten, die oft räumlich periodisch auf einer kleinen Skala auftreten. Die Homogenisierungstheorie ist eine Theorie singulärer Störungen. Sie liefert z.B. ‚effektive elastische Moduli‘ oder eine ‚effektive Leitfähigkeit‘ für das Gesamtmaterial. Intuitiv klar ist, dass zum Erreichen dieses Ziels eine Form von Mittelung nötig ist und dass die geometrische Anordnung der Konstituenten, z.B. in einem Laminat, in die Berechnung eingehen muss.

Wesentliches mathematisches Hilfsmittel ist die schwache Konvergenz. Insbesondere tritt das Problem auf, dass die Konvergenz von Produkten a_ku_k gezeigt werden muss, wobei die Funktionenfolgen (a_k)_k, (u_k)_k jeweils nur schwach konvergieren.

Inhalt: formale asymptotische Entwicklung, 1-d Fall, Laminate, Kompaktsheitslemma von Aubin-Lions, allgemeiner mehrdimensionaler Fall, Bestimmung der homogenisierten Matrix, Konvergenz gegen die homogenisierte Lösung, div - curl-Lemma, Zweiskalenkonvergenz, Verbesserung der Konvergenz: Korrektoren, Hashin-Shtrikman-Schranken, Fehlerabschätzungen, …

Literatur:

1.)

Cioranescu, D., Donato,P., An Introduction to Homogenization, Oxford University Press 1999

2.)

Vorlesungsskript von Prof. Ben Schweizer, U Dortmund, www.mathematik.uni-dortmund.de/lsi/schweizer/Skripte/

3.)

Tartar, L., The General Theory of Homogenization, Springer 2009

Inhalt:
Ziel des Kurses ist es, dass die Teilnehmer die Strukturierung von Projekten kennen und wissen, welchen Anforderungen sich Projektteams und -mitglieder stellen müssen.

Hierzu wird in Anlehnung an eine eingeführte Projektmanagementmethode zunächst die Strukturierung in Phasen und in Module innerhalb der Phasen vorgestellt. Die Arbeitsergebnisse, deliverables, der Module und die Bedingungen zum Abschluss der Phasen, milestones, sind das Grundgerüst zur Strukturierung von Projekten. Die Rollen der Projektbeteiligten werden angesprochen und diskutiert.

Anhand eines konkreten Projekts soll die Umsetzung in die Realität durchgeführt werden. Dabei sollen die Teilnehmer sich möglichst selbst in konkreten Projektsituationen erfahren und lernen auf typische, realitätsnahe Situationen vorbereitet zu sein.

Jede Projektmanagementmethode ist im Prinzip auf jedwede Art von Projekten anwendbar. In diesem Kurs wird die Anwendung in solchen Projekten im Mittelpunkt stehen, wo Geschäftsziele, business objectives, durch den Einsatz von IT-Systemen erreicht werden.

Der Kurs soll in den folgenden Semestern fortgesetzt werden, z.B. Anwendungsfelder mit spezifischen Anforderungen oder die vollständige Durchführung von konkreten Projekten.

Dieser Kurs wendet sich an Hörer aller Fakultäten. Er setzt voraus das Interesse an der Erreichung von Zielen in einem Team und die Bereitschaft und Offenheit sich als Person einzubringen. Er kann im Bachelor- und im Master-Studiengang der Mathematik als Wahlmodul eingebracht werden.___________________________________________________________________________________________

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden im BSc- oder MSc-Studiengang Mathematik, die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Bitte belegen Sie die Veranstaltung über das LSF bis Vorlesungsbeginn, und zwar die Gruppe desjenigen Dozenten, bei dem Sie tutorieren.

Leistungsnachweis:

• Teilnahme an der Einführungsveranstaltung (voraussichtlich in der ersten Vorlesungswoche; Termin wird den Teilnehmern per e-mail mitgeteilt)
• regelmäßige Teilnahme an der Tutorenbesprechung
• zwei gegenseitige Tutoratsbesuche mit einem anderen Modulteilnehmer, welcher nach Möglichkeit die gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der Einführungsveranstaltung)
• Schreiben eines Erfahrungsberichts, der an den betreuenden Dozenten geht

In Ermangelung eines passenden Wahlbereichs kann das Modul für Lehramtsstudierende in dieser Form zur Zeit nicht angeboten werden.__________________________________________________________

Inhalt:
Die Vorlesungen über Didaktik bestehen aus zwei Teilen: Didaktik der Algebra und Analysis (WS) und Didaktik der Geometrie und Stochastik (SS).

Eine scharfe Abgrenzung der Einzelthemen ist im schulischen Kontext wenig hilfreich. So wird z.B. die Projektion auf den ersten Blick der Geometrie zugeordnet, andererseits entsteht durch die Projektion einer Drehbewegung die Sinus- bzw. Kosinusfunktion. Im Sinne einer ganzheitlichen und vernetzenden Didaktik werden in der Vorlesung viele Bezüge zwischen den einzelnen, innermathematischen Disziplinen geschaffen.
Erörtert werden didaktische Methoden der Geometrie und Stochastik, die didaktische Bedeutung des Materials im schulischen Kontext sowie die Bedeutung von kooperativem Lernen (Gruppenarbeit). Zentral ist der Wechsel zwischen symbolischen, ikonischen und enaktiven Repräsentationsebenen (nach Bruner). An konkreten Beispielen wird ein konstruktivistischer Vermittlungsansatz im Kontext der bildungsplanspezifischen Inhalte (lernen, begründen, problemlösen und kommunizieren) aufgezeigt.
Die Vorlesung legt Wert darauf, dass die dargestellte Didaktik konkret und interaktiv erlebt wird. Die Folge ist ein ständiger Rollenwechsel des Hörers: Einerseits erlebt er die Dinge aus der Schülerperspektive, auf der anderen Seite schlüpft er in die Rolle des reflektierenden Lehrers.

Literatur:

1.)

Bauer, J.: Warum ich fühle, was Du fühlst; Hoffmann und Campe

2.)

Eichler A.; Vogel M.: Leitidee Daten und Zufall: Von konkreten Beispielen zur Didaktik der Stochastik; Wiesbaden: Vieweg + Teubner, 2009

3.)

Henn, J.: Geometrie und Algebra im Wechselspiel: Mathematische Theorie für schulische Fragestellungen; Springer Spektrum, 2012

4.)

Kramer, M.: Mathematik als Abenteuer; Aulis Verlag

5.)

Kramer, M.: Schule ist Theater; Schneider-Verlag Hohengehren

6.)

Spitzer, M.: Geist im Netz – Modelle für Lernen, Denken und Handeln; Spektrum Akademischer Verlag, Heidelberg

7.)

Thun, S. v.: Miteinander Reden, Bd. I–III; Rowohlt Tb.

Inhalt:
Ein Unterricht außerhalb des Klassenzimmers. Sei es auf dem Pausenhof, auf der Wiese vor der Schule, im Wald, in einem Mathe-Camp oder im Schullandheim. In Kleingruppen werden Lernumgebungen bzw. Erlebnisräume „jenseits des Klassenzimmers“ entworfen und durchgeführt.

Konkrete Inhalte:

1.

Handlungs- und erlebnisorientierte Didaktik, konstruktivistische und subjektive Didaktik

2.

Rollenverständnis (Rollen des Lehrers, Wechsel von Rollen, Rollenbelegung von mathematischen Inhalten)

3.

Gruppendynamik (Gruppenentwicklungsphasen)

4.

Gruppenarbeit, innere Struktur von Gruppen für das Fach Mathematik (Farbgruppen, Rollenverständnis)

5.

Kommunikation (Quadratische Nachrichten, inneres Team, Umgang mit mathematisch belasteten Schülern)

6.

Konkretes Erleben verschiedener Lernumgebungen (z.B. Schatzsuche mit Vektoren, Thaleskreis, Spielkasino, Brückenbau mit Erbsen und Zahnstochern, …)

7.

Studenten entwerfen eigene Erlebnisräume, die anschließend durchspielt werden.

8.

Mathematisierung eines Klettergartens.

Zur Unterkunft: Das Schwarzhornhaus bei Waldstetten (http://www.schwarzhornhaus.de/) ist ein Selbstversorgerhaus. Es wird gemeinsam gekocht. Übernachtet wird in Mehrbettzimmern (Schullandheim). Eigenen Bettbezug bitte mitbringen.

Kosten und Teilnehmerzahl: Die Eigenbeteiligung pro Person beträgt ca. 50–60 Euro. Maximal 24 Teilnehmer._____________________________________________________________________________________

Inhalt:
Das Seminar erarbeitet die notwendigen Grundkenntnisse die ein Unterrichtender an der Schule haben sollte im Bereich der Analysis und der Analytischen Geometrie und zeigt Beispiele für die Umsetzung im Unterricht.

Literatur:

1.)

Dankwerts, Vogel: Analysis verständlich unterrichten, Spektrum Akademischer Verlag Heidelberg, 2006

2.)

diverse Schulbücher der Oberstufe

Inhalt:
Der Einsatz von Unterrichtsmedien im Mathematikunterricht gewinnt sowohl auf der Ebene der Unterrichtsplanung, wie auch der der Unterrichtsrealisierung an Bedeutung. Vor dem Hintergrund konstruktivistischer Lerntheorien zeigt sich, dass der reflektierte Einsatz unter anderem von Computerprogrammen die mathematische Begriffsbildung nachhaltig unterstützen kann. So erlaubt beispielsweise das Experimentieren mit Computerprogrammen mathematische Strukturen zu entdecken, ohne dass dies von einzelnen Routineoperationen (wie z.B. Termumformung) überdeckt würde. Es ergeben sich daraus tiefgreifende Konsequenzen für den Mathematikunterricht. Von daher setzt sich dieses Seminar zum Ziel, den Studierenden die notwendigen Entscheidungs- und Handlungskompetenzen zu vermitteln, um zukünftige Mathematiklehrer auf ihre berufliche Tätigkeit vorzubereiten. Ausgehend von ersten Überlegungen zur Unterrichtsplanung werden anschließend Computer und Handheld hinsichtlich ihres jeweiligen didaktischen Potentials untersucht. Die dabei exemplarisch vorgestellten Systeme sind:

• dynamische Geometrie Software: Geogebra
• Tabellenkalkulation: Excel
• Handheld: GTR (Ti83), CAS (TI-Nspire)
• Software (elektronisches Schulbuch) und Lernprograme aus dem Internet.

Jeder Studierende soll eine Unterrichtssequenz ausarbeiten, die gegebenenfalls während einer Unterrichtsstunde erprobt wird.____________________________________________________________________________

Inhalt:
Die praktische Übung richtet sich an Hörer der Vorlesung Stochastik. Es werden computer-basierte Methoden diskutiert, die das Verständnis des Stoffes der Vorlesung vertiefen. Die praktische Übung wird auf der Basis des frei verfügbaren Statistik-Paketes R durchgeführt.

Nach einer Einführung in R werden Verfahren der deskriptiven Statistik und der graphischen Darstellung und Auswertung von Daten erläutert. Programmierkenntnisse werden nicht vorausgesetzt. Im zweiten Teil werden sowohl parametrische als auch nichtparametrische Testverfahren sowie Verfahren der linearen Regressions- und der Varianzanalyse diskutiert.

Die praktische Übung ist für Bachelor-Studierende verpflichtend.

Es werden die Laptops der Studierenden eingesetzt. Idealerweise sollte auf diesen dazu bereits R sowie ein VPN-Client für den Zugang zum WLAN der Uni Freiburg installiert sein. Entsprechende Links zum Download der Software sowie Hinweise zur Installation unter Linux, Mac OS X und Windows finden Sie auf der Webseite der Veranstaltung http://www.stochastik.uni-freiburg.de/Vorlesungen/vvSS2014/PraStoch/._________

Inhalt:
In der praktischen Übung zur Numerik-Vorlesung sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

R. Plato: Numerische Mathematik kompakt. Vieweg, 2006

2.)

R. Schaback, H. Wendland: Numerische Mathematik. Springer, 2004.

3.)

J. Stoer, R. Bulirsch: Numerische Mathematik I, II. Springer, 2007, 2005.

4.)

M. Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Vieweg+Teubner, 2006.

Inhalt:
In der praktischen Übung zur Vorlesung über die Numerik für Differentialgleichungen sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

R. Plato: Numerische Mathematik kompakt. Vieweg, 2006

2.)

R. Schaback, H. Wendland: Numerische Mathematik. Springer, 2004

3.)

J. Stoer, R. Bulirsch: Numerische Mathematik I, II. Springer, 2007, 2005

4.)

W. Walter: Gewöhnliche Differentialgleichungen: Eine Einführung. Springer, 2000

5.)

M. Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Vieweg+Teubner, 2006

Inhalt:
In dieser praktischen Übung werden die in der Vorlesung Theorie und Numerik partieller Differentialgleichungen II besprochenen Algorithmen implementiert und an praktischen Beispielen getestet.

Es sind Kenntnisse der Programmiersprache C erforderlich._______________________________________

Inhalt:
Wir wollen uns mit einer bunten Palette von Fragestellungen beschäftigen, die im Zusammenhang mit dem Stoff der Vorlesung Algebra und Zahlentheorie stehen, aber mit elementaren Methoden behandelt werden können.

Beispiele sind der euklidische Algorithmus, Kettenbrüche, Zahnräder, lineare und quadratische Gleichungssysteme über den ganzen Zahlen.

Literatur:

1.)

G. Frey, Elementare Zahlentheorie

Inhalt:

Das Proseminar soll parallel zur Vorlesung Topologie laufen und sie durch allerhand nette Anwendungen ergänzen.

Literatur:

1.)

M.A. Armstrong, Basic Topologie, Springer 1983

2.)

K. Jänich, Topologie, Springer 2001

3.)

E. Ossa, Topologie, Vieweg + Teubner 2009

4.)

W. Soergel, Skriptum Topologie

Inhalt:
Es wird nach dem Skript ,,Kreise” von Wolf Barth gearbeitet. Es handelt sich um die Geometrie der Kreise und Familien von Kreisen. Das Stoff ist mit elementaren Methoden zugänglich.

In je einem Vortrag soll ein Abschnitt aus dem Skript besprochen werden. Gruppenarbeit (zu zweit) wird erwünscht.

Literatur:

1.)

Barth, W.: Kreise,, Erlangen 2010, zugänglich unter

https://dl.dropbox.com/u/103692683/Kreiset.pdf

Inhalt:
Eine Darstellung einer Gruppe G ist ein Homomorphismus

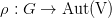
von G in die Automorphismengruppe eines Vektorraums V . Wir beschränken uns auf endliche Gruppen und endlich-dimensionale Vektorräume über den komplexen Zahlen.

Eine Darstellung heißt irreduzibel, wenn V nicht null ist und wenn V außer 0 keinen echten Unterraum hat, der unter allen ρ(g) invariant ist. Die irreduziblen Darstellungen einer abelschen Gruppen sind genau die 1-dimensionalen Darstellungen, das heißt die Homomorphismen von G in die multiplikative Gruppe der komplexen Zahlen. Man zeigt:

• Jede Darstellung ist direkte Summe von irreduziblen Darstellungen.
• G hat ebensoviele irreduzible Darstellungen wie Konjugationsklassen.

Der Charakter einer Darstellung ρ ordnet jeder Konjugationsklasse g^G die Spur von ρ(g) zu. Eine Darstellung ist durch ihren Charakter eindeutig bestimmt. Die Charaktere irreduzibler Darstellungen haben Orthogonalitäts– und Ganzheitseigenschaften, die es erleichtern, die Charaktere aller irreduziblen Darstellungen zu bestimmen.

Am Schluß werden wir alle irreduziblen Darstellungen der symmetrischen Gruppe S_n berechnen.

Literatur:

1.)

Ziegler Skript Algebra
http://home.mathematik.uni-freiburg.de/ziegler/skripte/algebra.pdf

2.)

Jacobson, Basic Algebra II

Inhalt:
Im Seminar sollen adaptive Methoden zur automatischen Diskretisierung partieller Differentialgleichungen diskutiert werden. Diese Verfahren führen eine lokale Verfeinerung einer zugrundeliegenden Finite-Elemente-Triangulierung basierend auf sogenannten Verfeinerungsindikatoren durch und ermöglichen damit optimale Konvergenzresultate auch bei singulären Lösungen.

Literatur:

1.)

S. Bartels: Adaptive Methods for Partial Differential Equations, Vorlesungsskript.

2.)

R. Verfürth: A Posteriori Error Estimation Techniques for Finite Element Methods, Oxford University Press, 2013.

Inhalt:
Das Seminar behandelt neuere Ergebnisse über NTP₂-Theorien. Das sind vollständige Theorien, in denen es für keine Formel ϕ(x,y) eine unendliche Matrix (a_i,j) von Parametern gibt, sodaß

• für jedes f : ℕ → ℕ die Menge {ϕ(x,a_i,f(i))∣i ∈ ℕ} konsistent ist,
• für jedes i die Menge {ϕ(x,a_i,j)∣j ∈ ℕ} k-inkonsistent ist.

Der Begriff der NTP₂-Theorien umfaßt die Klasse der einfachen und die Klasse der o-minimalen Theorien. Für einen Survey siehe http://www.academia.edu/2760510/NTP2.

Literatur:

1.)

H. Adler, Strong theories and weight, Preprint March 2007,
http://www.logic.univie.ac.at/~adler/Publications.html

2.)

I. Ben-Yaacov and A. Chernikov, An independence theorem for NTP₂ theories, arXiv:1207.0289. Aug. 2013.

3.)

A. Chernikov, Theories without the tree property of the second kind, Annals Pure and App. Logic 165 (2014) 695–723.

4.)

A. Chernikov and I. Kaplan, Forking and dividing in NTP₂ theories J. Symbolic Logic 77 (2012) 1-20.

5.)

K. Tent and M. Ziegler, A Course in Model Theory, Lecture Notes in Logic 40, Cambridge UP 2012.

Inhalt:
Infinite games are a sort of abstract infinitary formulation of the well-known two-players games that one easily encounters in real life, like chess, checkers, and so on. Despite their very simple definition, in the last 50 years they have proven to be a remarkably powerful and versatile technique, with many applications in various areas of mathematics, including topology, set theory, measure theory, inner model theory, and so on. In this seminar we will study this method from both the theoretical point of view (determinacy and its interactions with the other axioms of set theory), and the applied one (connections with topological and measure-theoretic properties, Wadge theory, and so on).

Literatur:

1.)

Alessandro Andretta, Wadge Degrees, available at http://home.mathematik.uni-freiburg.de/mottoros/ss14gametheory.html.

2.)

Alexander A. Kechris, Classical descriptive set theory, volume 156 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1995.

3.)

Yiannis N. Moschovakis. Descriptive Set Theory. North Holland, Amsterdam, New York, Oxford, 1980.

4.)

Robert A. Van Wesep. Wadge degrees and descriptive set theory. In Alexander S. Kechris and Yiannis N. Moschovakis, editors, Cabal Seminar 76–77, number 689 in Lecture Notes in Mathematics. Springer-Verlag, 1978.

Inhalt:
In diesem Seminar beschäftigen wir uns zunächst mit Vektorbündeln über topologischen Räumen und Abbildungen zwischen ihnen. Bis auf Isomorphie lassen sich Vektorbündel über hinreichend schönen Räumen X mit Homotopieklassen von Abbildungen von X in einen klassifizierenden Raum identifizieren. Man kann Vektorbündel über X addieren und multiplizieren und so — wie beim Übergang von natürlichen zu ganzen Zahlen — einen Ring K(X) definieren. Wir konstruieren unter anderem Thom-Isomorphismen und beweisen Bott-Periodizität. Durch diese und weitere Eigenschaften wird K-Theorie zu einem ähnlich mächtigen Werkzeug in der Topologie wie etwa die singuläre Kohomologie.

Der Atiyah-Singer-Indexsatz macht Aussagen über die Lösungsräume gewisser linearer Differentialgleichungen auf Mannigfaltigkeiten. Seine Anwendungen reichen von der Analysis bis in die algebraische Geometrie. Im zweiten Teil des Seminars wollen wir diesen Satz als ein K-theoretisches Problem formulieren und mit den Methoden aus dem ersten Teil beweisen.

Literatur:

1.)

Atiyah, M. F., K-Theory, Addison-Wesley Publishing Company, 1989

2.)

Bleecker, D. D., Booß-Bavnbek, B., Index theory—with applications to mathematics and physics, International Press, 2013

3.)

Hatcher, A., Vector Bundles and K-Theory, http://www.math.cornell.edu/~hatcher/VBKT/VBpage.html

4.)

Lawson, H. B., Michelsohn, M.-L., Spin Geometry, Princeton University Press, 1989

5.)

Shanahan, P., The Atiyah-Singer Index Theorem, Lecture Notes 638, Springer, 1978

Inhalt:
Dieses Seminar richtet sich insbesondere an Studierende im Masterstudiengang bzw. Hauptstudium. Wir werden aufbauend auf den Vorlesungen zur Theorie und Numerik für partielle Differentialgliechungen weiterführende Resultate besprechen.__________________________

Inhalt:
Es sollen Randwertprobleme für zweidimensionale parametrisierte Flächen studiert werden, die ein Randwertproblem lösen. Es werden Arbeiten zu Minimalflächen und Flächen konstanter mittlerer Krümmung sowie zu Willmoreflächen betrachtet. Zentrale Fragen sind die Existenz und Eindeutigkeit der Lösungen. Das Seminar geht nach Originalliteratur vor, die bei der Vorbesprechung genannt wird.

Literatur:

1.)

Dierkes, U. et al.: Minimal Surfaces I, Boundary Value Problems, Springer 1992

Inhalt:
Aufbauend auf der Vorlesung Wahrscheinlichkeitstheorie werden in dieser Veranstaltung Themen von Bachelor-Arbeiten vorgestellt. Die Themen können sowohl direkt an die Vorlesung Wahrscheinlichkeitstheorie anschließen, als auch Anwendungen enthalten, z.B. aus den Themenbereichen Finanzmathematik, Statistik, biologische Prozesse und zufällige Algorithmen.____________________________________________________________________________________________________

Inhalt:
Thema des Seminars ist eine Einführung in Methoden und Anwendungen der Asymptotischen Statistik. Die asymptotische Statistik ermöglicht es, unter allgemeinen Voraussetzungen (approximativ) optimale statistische Verfahren zu bestimmen. Das Seminar behandelt die grundlegenden Methoden (Begriff der asymptotischen Effizienz, lokale asymptotische Normalität, Limes von Experimenten) wie auch relevante Beispielklassen (semiparametrische Modelle).

Literatur:

1.)

van der Vaart: Asymptotic Statistics, 2000

2.)

Kosarok: Introduction to Empirical Processes and Semiparametric Inference, 2008

Inhalt:

Viele Fragestellungen aus Naturwissenschaft und Technik führen auf nichtlineare partielle Differentialgleichungen. Im Seminar werden wir auf Grundlage von Originalartikeln Techniken und Methoden zur Behandlung von elliptischen und parabolischen Gleichungen erarbeiten, die über den Stoff der Vorlesung „Nichtlineare Funktionalanalysis“ hinausgehen.

Die behandelten Themen eignen sich sowohl als Grundlage für Bachelor- als auch für Masterarbeiten._________________________________________________________________________________________________

Inhalt:
Maximumprinzipien gestatten mit relativ geringem technischen Aufwand den Beweis manch interessanten und sehr anschaulichen Resultats über die Gestalt von Lösungen vor allem elliptischer („Laplace“) und parabolischer („Wärmeleitung“) Differentialgleichungen.

Literatur:

1.)

D. Gilbarg, N.S. Trudinger, Elliptic partial differential equations of second order, 2nd edition, Berlin etc.: Springer-Verlag, 1983.

2.)

J. Serrin, A symmetry problem in potential theory, Arch. Rational Mech. Anal. 43, 304–318 (1971).

3.)

H. Weinberger, Remark on the preceding paper by Serrin, Arch. Rational Mech. Anal. 43, 319–320 (1971).

4.)

R. Finn, Equilibrium Capillary Surfaces, New York etc.: Springer-Verlag, 1986.

5.)

B. Kawohl, Rearrangements and Convexity of Level Sets in PDE, Lecture Notes in Mathematics 1150, Berlin etc.: Springer-Verlag, 1985.

6.)

B. Gidas, W.-M. Ni, L. Nirenberg, Symmetry and related properties via the maximum principle, Commun. Math. Phys. 68, 209–243 (1979).

7.)

A. Bennett, Symmetry in an overdetermined fourth order elliptic boundary value problem, SIAM J. Math. Anal. 17, 1354–1358 (1986).

8.)

Chen, Wen Xiong; Li, Congming, Classification of solutions of some nonlinear elliptic equations. Duke Math. J. 63 (1991), no. 3, 615–622.

9.)

F. Gazzola, H.-Ch. Grunau, Critical dimensions and higher order Sobolev inequalities with remainder terms, Nonl. Differ. Equ. Appl. NoDEA 8, 35–44 (2001).

Inhalt:

Aus der Differentialgeometrie wissen wir, dass die abgebildeten Kachelungen der Sphäre und der hyperbolischen Ebene (im Poincaréschen Ballmodell) als Veranschaulichung von nicht-euklidischen Geometrien dienen. Ein sehr schönes und erstaunliches Resultat von Schwarz ist nun, dass die Kachelungen mit Hilfe der Funktionentheorie durch eine lineare Differentialgleichung zweiter Ordnung charakterisiert werden können, nämlich der hypergeometrischen Differentialgleichung

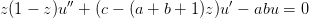
Das Faszinierende bei ihrer Untersuchung ist, dass Verbindungen zu ganz unterschiedliche Gebieten der Mathematik auftreten: Funktionentheorie, Gruppentheorie, Topologie, algebraische Geometrie und Differentialgeometrie. Das Ziel dieses Seminars ist, diese Verbindungen aufzudecken und den Zusammenhang zu obigen Kachelungen zu verstehen.

Literatur:

1.)

Iwasaki, K., Kimura, H., Shimomura, S., Yoshida, M.: From Gauß to Painlevé, Vieweg.

2.)

Yoshida, M.: Hypergeometric functions, My Love, Vieweg.

3.)

Freitag, Busam: Funktionentheorie I, II. Springer

4.)

Walter: Gewöhnliche Differentialgleichungen. Springer.

Inhalt:
Moderne statistische Methoden und Modellierungstechniken im Bereich der Biostatistik adressieren komplexe Fragestellungen in den biomedizinischen Wissenschaften, wie z.B. die Einbeziehung molekularer Information in Studien zur Ätiologie, Diagnose/Prognose und Therapie. Eine Auswahl solcher Problemstellungen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren.

Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als Einführung in die Thematik dienen.

Das Hauptseminar ist terminlich und inhaltlich mit dem Oberseminar „Medizinische Statistik“ abgestimmt.

Literatur wird in der Vorbesprechung bekannt gegeben.

Das Seminar beginnt am 30.04.2014 und endet mit dem 30.07.2014._____________________________

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann.

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe (einem Oberseminar, Projektseminar …)) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im Vertiefungsmodul wird der Stoff des Lesekurses in der mündlichen Abschlussprüfung zusammen mit dem weiteren Stoff abgeprüft.__________________________________

Inhalt:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology or mathematical physics or a mix thereof.

The precise topic will be chosen at the end of the preceeding semester. The program will be made available via our web site.

The level is aimed at our doctoral students. Master students are very welcome to participate as well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. A. Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________

Inhalt:
The Joint Seminar is a research seminar in complex and algebraic geometry, organized by the research groups in Freiburg, Nancy and Strasbourg. The seminar meets roughly twice per semester in Strasbourg, for a full day. There are about four talks per meeting, both by invited guests and by speakers from the organizing universities. We aim to leave ample room for discussions and for a friendly chat.

The talks are open for everyone. Contact one of the organizers if you are interested in attending the meeting. We have some (very limited) funds that might help to support travel for some junior participants.____________________________________________________________________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17:00 Uhr im Hörsaal II in der Albertstr. 23 b statt.

Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Eckerstraße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/