12.8 Konvergenz in zufälligen Graphen
Seminar: | Konvergenz in zufälligen Graphen |
| | |
Dozent: | Prof. Dr. Ludger Rüschendorf |
| | |
Zeit/Ort: | Di 16–18 Uhr, SR 127, Eckerstr. 1 |
| | |
Tutorium: | Viktor Wolf |
| | |
Vorbesprechung: | Mo 8. Febr. 2010, 13:30 Uhr, Zi. 232, Eckerstr. 1 |
| | |
Teilnehmerliste: | Eintrag in eine Liste im Sekretariat (Zi. 226 bzw. 245, Eckerstr. 1)
bis zum 5. Febr. 2010. |
| | |
Web-Seite: |
http://www.stochastik.uni-freiburg.de/ |
| | |
| |
_____________________________________________________________________
Inhalt:
Thema des Seminars ist die Analyse von euklidischen Funktionalen in
zufälligen Graphen. Behandelt werden insbesondere Eigenschaften von
Lösungen für Probleme der euklidischen kombinatorischen Optimierung wie
z.B. das Problem der kürzesten Tour durch eine zufällige Punktmenge im
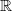 d oder minimale Spannbäume und Matchings. Die dazu angewandte
Methodik – sub- und super-additive Funktionale, isoperimetrische und
Konzentrationsungleichungen – wird in dem Seminar im Detail behandelt.
Es stellt sich heraus, daß in stochastischen Graphen für eine Reihe von
Optimierungsproblemen präzise Asymptotiken gefunden werden können.
Das ist recht überraschend, weil zu dem entsprechenden Problem für
deterministische Graphen in der Regel keine Ergebnisse bekannt
sind.
d oder minimale Spannbäume und Matchings. Die dazu angewandte
Methodik – sub- und super-additive Funktionale, isoperimetrische und
Konzentrationsungleichungen – wird in dem Seminar im Detail behandelt.
Es stellt sich heraus, daß in stochastischen Graphen für eine Reihe von
Optimierungsproblemen präzise Asymptotiken gefunden werden können.
Das ist recht überraschend, weil zu dem entsprechenden Problem für
deterministische Graphen in der Regel keine Ergebnisse bekannt
sind.
Literatur:
- Yukich, J. E.: Probability Theory of Classical Euclidean Optimization
Problems. Lecture Notes in Mathematics 1675. Berlin (Springer) 1998
- Penrose, M. D.: A central limit theorem with application to percolation,
epidemics and Boolean models. Ann. Prob. 29, 1515–1546, 2001
- Penrose, M. D.; Yukich, J. E.: Central limit theorems for some graphs
in computational geometry. Ann. Appl. Prob. 11, 1005–1041, 2001
_____________________________________________________________________
Typisches Semester: | 6. Semester |
Notwendige Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Sprechstunde Dozent: | Di 11–12, Zi. 242, Eckerstr. 1 |
Sprechstunde Assistent: | Do 15–16 und n.V., Eckerstr. 1 |
| |
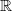 d oder minimale Spannbäume und Matchings. Die dazu angewandte
Methodik – sub- und super-additive Funktionale, isoperimetrische und
Konzentrationsungleichungen – wird in dem Seminar im Detail behandelt.
Es stellt sich heraus, daß in stochastischen Graphen für eine Reihe von
Optimierungsproblemen präzise Asymptotiken gefunden werden können.
Das ist recht überraschend, weil zu dem entsprechenden Problem für
deterministische Graphen in der Regel keine Ergebnisse bekannt
sind.
d oder minimale Spannbäume und Matchings. Die dazu angewandte
Methodik – sub- und super-additive Funktionale, isoperimetrische und
Konzentrationsungleichungen – wird in dem Seminar im Detail behandelt.
Es stellt sich heraus, daß in stochastischen Graphen für eine Reihe von
Optimierungsproblemen präzise Asymptotiken gefunden werden können.
Das ist recht überraschend, weil zu dem entsprechenden Problem für
deterministische Graphen in der Regel keine Ergebnisse bekannt
sind.