Vorlesung: | Variationsrechnung |
Dozentin: | Paola Pozzi, PhD |
Zeit/Ort: | Di 9–11, Do 9–10 Uhr, SR 226, Hermann-Herder-Str. 10 |
Übungen: | Do 10–11 Uhr, SR 226, Hermann-Herder-Str. 10 |
Web-Seite: | http://aam.mathematik.uni-freiburg.de/IAM/homepages/paola/ |
Inhalt:
Das Ziel der Variationsrechnung ist es optimale Lösungen eines Problems zu
finden und ihre Eigenschaften zu beschreiben. Die Variationsrechnung spielt
in Geometrie, Physik und Numerik eine wichtige Rolle. Die Vorlesung ist
eine Einführung in die mehrdimensionale Variationsrechnung. In diesem
klassischen Gebiet der Analysis geht es um das Auffinden von Minima -
oder allgemeiner von Extrema - von Funktionalen, die meist die
Form
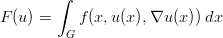
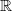 n und die Funktion f
gegeben. Ganz ähnlich wie beim Bestimmen von Extremwerten von
Funktionen leiten wir notwendige Bedingungen für die Extrema von F her.
Dazu muss man wissen, was eine Bedingung der Form
n und die Funktion f
gegeben. Ganz ähnlich wie beim Bestimmen von Extremwerten von
Funktionen leiten wir notwendige Bedingungen für die Extrema von F her.
Dazu muss man wissen, was eine Bedingung der Form
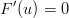
Typisches Semester: | ab 5. Semester |
Studienschwerpunkt: | Angewandte Mathematik |
Notwendige Vorkenntnisse: | Die Grundvorlesungen einschließlich Analysis III |
Nützliche Vorkenntnisse: | Funktionalanalysis, partielle Differentialgleichungen |
Sprechstunde Dozentin: | Di 16–17 Uhr, Raum 223, Hermann-Herder-Str.10 |