[next] [prev] [prev-tail] [tail] [up]

3.2 p-adische Zahlen

Proseminar:

p-adische Zahlen

  

Dozentin:

Prof. Huber-Klawitter

  

Zeit/Ort:

Do 11–13 Uhr, SR 404, Eckerstr. 1

  

Tutorium:

Dipl. Math. Jakob Scholbach

  

Vorbesprechung:

Mittwoch, 2. April 2008, um 10 Uhr ct., Raum 434

  

Teilnehmerliste:

Bei Frau Gilg (Zi. 433, Eckerstr. 1, vormittags)

  

Inhalt:

Auf den rationalen Zahlen gibt es neben dem gewöhnlichen Absolutbetrag auch noch weitere Beträge, nämlich für jede Primzahl p den p-adischen Betrag. Ist x = x′pi mit Zähler und Nenner von x′ teilerfremd zu p und i ∈ Z, so setzen wir

-i |x|p = p

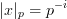
Eine Zahl ist also klein, wenn sie durch eine hohe Potenz von p geteilt wird. Die p-adischen Zahlen Qp erhalten wir aus Q durch Komplettieren bezüglich dieses Betrages, genau wie man R durch Komplettieren am gewöhnlichen Absolutbetrag erhält. Mit den p-adischen Zahlen kann man dann genauso Analysis betreiben wie mit R: Folgen, Reihen, Konvergenz, Stetigkeit,…

Die vertraute Sprache der Analysis wird letztlich benutzt, um zahlentheoretische Eigenschaften von Zahlen zu studieren. Daher sind die p-adischen Zahlen nicht nur Spielerei, sondern ein sehr wichtiges Objekt der Zahlentheorie.

Im Proseminar sollen die p-adischen Zahlen eingeführt werden und ihre grundlegenden Eigenschaften studiert werden. Wir werden sehen, wie weit die Theorie genauso funktioniert wie über R, und was anders ist.

Literatur:

  1. N. Koblitz, p-adic Numbers, p-adic Analysis, and Zeta Functions, 2nd Edition, Springer 1984
  2. J.-P. Serre, A course in Arithmetic, Springer 1973

Typisches Semester:

2.-4. Semester

Studienschwerpunkt:

alle

Notwendige Vorkenntnisse:

Analysis I, Lineare Algebra I

Sprechstunde Dozentin:

wird noch bekanntgegeben

Sprechstunde Assistent:

wird noch bekanntgegeben

Kommentar:

Interessenten, die zum Vorbesprechungstermin verhindert sind, melden sich bitte per Email an: huber@mathematik.uni-leipzig.de

[next] [prev] [prev-tail] [front] [up]