Lehrveranstaltungen
1. Vorlesungen

WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Inhalt der Vorlesung Analysis III ist die Maß- und Integrationstheorie unter besonderer
Berücksichtigung des Lebesgue-Maßes. Diese Theorien sind von besonderer Bedeutung für viele
weiterführende Vorlesungen aus der Analysis, Angewandten Mathematik, Stochastik,
Wahrscheinlichkeitstheorie und Geometrie wie auch der Physik. Themenschwerpunkte sind
Maße und Integrale im ℝn, Lebesgueräume, Konvergenzsätze, der Transformationssatz,
Oberflächenintegrale und der Integralsatz von Gauss.
Literatur:
-
1.)
- Heuser, H.: Lehrbuch der Analysis, Teil 2 (14. Aufl.), Vieweg + Teubner (2008)
-
2.)
- Königsberger, K.: Analysis 2 (5. Aufl.), Springer (2004)
(Weitere Literatur wird innerhalb der Vorlesung angegeben werden.)____________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Pflichtveranstaltung im B.Sc. Mathematik
Wahlmodul im Optionsbereich des 2-Hf-Bachelor (sofern keine
Lehramtsoption angestrebt wird)
Wahlpflichtmodul Mathematische Vertiefung im M.Ed. |
Notwendige Vorkenntnisse: | Analysis I, II |
Nützliche Vorkenntnisse: | Lineare Algebra II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Diese Vorlesung setzt die Lineare Algebra fort. Behandelt werden Gruppen, Ringe, Körper sowie
Anwendungen in der Zahlentheorie und Geometrie. Höhepunkte der Vorlesung sind die
Klassifikation endlicher Körper, die Unmöglichkeit der Winkeldreiteilung mit Zirkel und Lineal,
die Nicht-Existenz von Lösungsformeln für allgemeine Gleichungen fünften Grades und das
quadratische Reziprozitätsgesetz.
Literatur:
-
1.)
- Michael Artin: Algebra, Birkhäuser (1998)
-
2.)
- Siegfried Bosch: Algebra (8. Aufl.), Springer Spektrum (2013)
-
3.)
- Serge Lang: Algebra (3. Aufl.), Springer (2002)
-
4.)
- Wolfgang Soergel: Skript Algebra und Zahlentheorie
____________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie II
Pflichtveranstaltung im 2-Hf-Bachelor |
Notwendige Vorkenntnisse: | Lineare Algebra I, II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die algebraische Topologie untersucht topologische Räume mit algebraischen Methoden.
Typische Fragen sind
- Gibt es (topologische) Räume mit den Eigenschaften …?
- Gibt es (stetige) Abbildungen von X nach Y mit den Eigenschaften …?
- Sind zwei gegebene Räume oder Abbildungen in einem gewissen Sinne „gleich“?
Methoden der algebraischen Topologie werden in vielen Bereichen der Mathematik, insbesondere
in der Geometrie, eingesetzt.
In der Vorlesung betrachten wir als erstes die Fundamentalgruppe und höhere Homotopiegruppen.
Als Anwendungen erhalten wir einige klassische Sätze, zum Beispiel den Brouwerschen
Fixpunktsatz. Homotopiegruppen sind zwar sehr mächtige Invarianten, in der Praxis aber nicht
einfach zu bestimmen.
Homologie- und Kohomologiegruppen sind mit Homotopiegruppen entfernt verwandt,
lassen sich aber besser axiomatisch charakterisieren und leichter berechnen. Sie tragen
zusätzliche Strukturen, zum Beispiel das Cup-Produkt auf der Kohomologie. Wir
wollen diese Invarianten in einer Sprache beschreiben, die sich später auch für andere
topologische Konstruktionen wie K-Theorie, stabile Homotopie und Kobordismus benutzen
lässt.
Bei Interesse wird die Vorlesung im SS 2020 fortgesetzt. Wir werden dann unter anderem
Poincaré-Dualität für topologische Mannigfaltigkeiten kennenlernen.
Literatur:
-
1.)
- T. tom Dieck: Algebraic Topology, EMS Textbooks in Mathematics, EMS, Zürich, 2008.
-
2.)
- A. Hatcher: Algebraic Topology, Cambridge University Press, 2002,
http://www.math.cornell.edu/~hatcher/AT/ATpage.html
__________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Topologie |
Folgeveranstaltungen: | Algebraische Topologie II, s.o. |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die Differentialgeometrie untersucht geometrische Eigenschaften gekrümmter Räume mit
Methoden der Differentialrechnung. Sie hat Anwendungen in anderen Bereichen der Mathematik
und in der Physik, etwa in der theoretischen Mechanik und der Relativitätstheorie.
In der Vorlesung wird eine Einführung in die (Semi-)Riemannsche Geometrie gegeben. Hier
werden insbesondere Geodätische und der Riemannsche Krümmungstensor im Mittelpunkt
stehen.
Literatur:
-
1.)
- Barrett O’Neill, Semi-Riemannian Geometry with Applications to Relativity, Academic Press,
1983
-
2.)
- J.M. Lee, Introduction to Smooth Manifolds, Springer (GTM 218), 2003
-
3.)
- M.P. do Carmo, Riemannian Geometry, Birkhäuser, 1992
_____________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Analysis I+II, Lineare Algebra I+II, Analysis III oder
Elementare Differentialgeometrie |
Folgeveranstaltungen: | Differentialgeometrie II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Einführung in Theorie und Numerik partieller
Differentialgleichungen |
| | |
Dozent: | Prof. Dr. M. Růžička |
| | |
Zeit/Ort: | Mo, Mi 10–12 Uhr, HS II, Albertstr. 23b |
| | |
Übungen: | 2-std. n. V. |
| | |
Tutorium: | Dr. M. Křepela |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agru/lehre/index.html |
| | |
| |
_______________________________________________________________
Inhalt:
Diese Vorlesung ist die erste eines Kurses von aufeinander aufbauenden Vorlesungen zur Theorie
und Numerik partieller Differentialgleichungen.
Partielle Differentialgleichungen treten oft als Modelle für physikalische Vorgänge auf, z. B. bei
der Bestimmung einer Temperaturverteilung, bei der Beschreibung von Schwingungen von
Membranen oder Strömungen von Flüssigkeiten.
In dieser Vorlesung werden wir uns mit elliptischen Differentialgleichungen beschäftigen. Es wird
sowohl die klassische Existenztheorie als auch die moderne Theorie zur Lösbarkeit solcher
Gleichungen behandelt. Selbst wenn man für einfache Probleme explizite Lösungsformeln hat,
können diese nur selten auch konkret berechnet werden. Deshalb ist es wichtig, numerisch
approximative Lösungen zu berechnen und nachzuweisen, dass diese in geeigneter Weise gegen
die exakte Lösung konvergieren. Dazu wird in der Vorlessung die entsprechende Theorie Finiter
Elemente dargestellt.
Parallel zu der Vorlesung wird ein Praktikum (siehe Kommentar zum Praktikum)
angeboten.
Literatur:
-
1.)
- Evans, Partial Differential equations, AMS (1998).
-
2.)
- Braess, Finite Elemente, Springer (1992).
-
3.)
- Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010).
____________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Analysis I-III, LA I, II |
Nützliche Vorkenntnisse: | Funktionalanalysis |
Folgeveranstaltungen: | Nichtlineare Funktionalanalysis, Theorie und Numerik
partieller Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die klassische Funktionentheorie untersucht komplex differenzierbare Funktionen in einer
Veränderlichen, die auf einer offenen Menge in der komplexen Ebene ℂ definiert sind. Man
arbeitet auch häufig auf der Riemannschen Zahlenkugel, die aus ℂ durch Hinzufügung eines
Punktes im Unendlichen entsteht, und man lässt isolierte Singularitäten zu. Als natürliche
Verallgemeinerung ergibt sich nun die Untersuchung komplex differenzierbarer Funktionen auf
offenen Teilmengen anderer, sogenannter Riemannscher Flächen, anstelle der Riemannschen
Zahlenkugel. Die einfachsten Beispiele sind die elliptischen Kurven und die dazugehörigen
doppelt periodischen Funktionen auf ℂ. Allgemeiner fügt man der oberen komplexen Halbebene
geeignete Punkte hinzu und fordert von den holomorphen Funktionen ein spezielles
Transformationsverhalten unter bestimmten Möbiustransformationen, um die sogenannten
Modulformen zu definieren. Modulformen können dann als Bausteine für die Konstruktion
holomorpher und meromorpher Funktionen auf Riemannschen Flächen angesehen werden. Die
sogenannte Diskriminantenfunktion
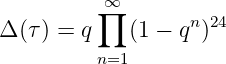 mit
q = exp(2πiτ) für τ in der oberen komplexen Halbebene ist ein klassisches Beispiel einer
Modulform, das zudem einen für Modulformen typischen Zusammenhang zu einem Zählproblem
aufweist:
mit
q = exp(2πiτ) für τ in der oberen komplexen Halbebene ist ein klassisches Beispiel einer
Modulform, das zudem einen für Modulformen typischen Zusammenhang zu einem Zählproblem
aufweist:
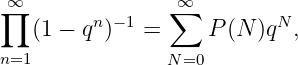 wobei P(N) die Anzahl der Partitionen von N angibt.
wobei P(N) die Anzahl der Partitionen von N angibt.
Die Vorlesung gibt eine elementare Einführung in die Theorie der elliptischen Funktionen, der
elliptischen Kurven und der Modulformen mit Blick auf den Zusammenhang zu kompakten
Riemannsche Flächen im Allgemeinen.
Literatur:
-
1.)
- J.H. Bruinier, G. v.d. Geer, G. Harder, D. Zagier, The 1-2-3 of Modular Forms, Springer
2008
-
2.)
- F. Diamond, J. Shurman, A First Course in Modular Forms, Springer 2005
-
3.)
- M. Eichler, D. Zagier, The Theory of Jacobi Forms, Birkhäuser 1985
-
4.)
- N. Koblitz, Introduction to Elliptic Curves and Modular Forms, Springer 1984
-
5.)
- K. Lamotke, Riemannsche Flächen, Springer 2009
______________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Funktionentheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die Vorlesung Mathematische Statistik baut auf Grundkenntnissen aus der Vorlesung
Wahrscheinlichkeitstheorie auf. Das grundlegende Problem der Statistik ist, anhand einer
Stichprobe von Beobachtungen möglichst präzise Aussagen über den datengenerierenden Prozess
bzw. die den Daten zugrundeliegenden Verteilungen zu machen. Hierzu werden in der Vorlesung
die wichtigsten Methoden aus der statistischen Entscheidungstheorie wie Test-und
Schätzverfahren eingeführt. Stichworte hierzu sind u.a. Bayes-Schätzer und -Tests,
Neyman-Pearson-Testtheorie, Maximum-Likelihood-Schätzer, UMVU-Schätzer, exponentielle
Familien, lineare Modelle.
Weitere Themen sind Ordnungsprinzipien zur Reduktion der Komplexität der Modelle
(Suffizienz und Invarianz). Sofern Zeit bleibt, sollen auch einige Verfahren zur
Zeitreihenmodellierung und -Analyse (ARMA- und GARCH-Prozesse) näher vorgestellt und
untersucht werden.
Literatur:
-
1.)
- Brockwell, P.J., Davis, R.A.: Time Series: Theory and Mehods (Second Edition), Springer
(1991)
-
2.)
- Czado, C., Schmidt, T.: Mathematische Statistik, Springer (2011)
-
3.)
- Rüschendorf, L.: Mathematische Statistik, Springer Spektrum (2014)
-
4.)
- Schervish, M.J.: Theory of Statistics, Springer (1997)
-
5.)
- Witting, H.: Mathematische Statistik I, Teubner (1985)
_____________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Mathematische Logik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
In dieser Vorlesung werden die Grundlagen der geometrischen Modelltheorie behandelt.
Grundbegriffe wie Quantorenelimination oder Kategorizität werden eingeführt. Eine Theorie hat
Quantorenelimination, falls jede Formel äquivalent zu einer quantorenfreien Formel ist. Für die
Theorie algebraisch abgeschlossener Körper einer festen Charakteristik ist dies dazu äquivalent,
dass die Projektion einer Zariski-konstruktiblen Menge wiederum Zariski-konstruktibel
ist.
Eine Theorie heiße ℵ1-kategorisch, wenn alle Modelle der Mächtigkeit ℵ1 isomorph sind. Ein
typisches Beispiel ist die Theorie unendlich dimensionaler ℚ-Vektorräume. Das Ziel der
Vorlesung ist es, die Sätze von Baldwin-Lachlan und von Morley zu verstehen, um
ℵ1-kategorische Theorien zu charakterisieren.
Literatur:
-
1.)
- B. Poizat : Cours de théorie des modèles, (1985), Nur al-Mantiq wal-Ma’rifah.
-
2.)
- K. Tent, M. Ziegler: A Course in Model Theory, (2012), Cambridge University Pres.
__________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Mathematische Logik |
Nützliche Vorkenntnisse: | Algebra und Zahlentheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die Vorlesung schließt direkt an die Vorlesung Wahrscheinlichkeitstheorie aus dem WS 2018/19
an.
Ein stochastischer Prozess (Xt)t∈I ist nichts weiter als eine Familie von Zufallsvariablen, wobei
etwa I = [0,∞) eine kontinuierliche Zeitmenge ist. Einfache Beispiele sind Irrfahrten,
Markov-Ketten, die Brown’sche Bewegung oder davon abgeleitete Prozesse. Letztere spielen vor
allem in der Modellierung von finanzmathematischen oder naturwissenschaftlichen
Fragestellungen eine große Rolle.
Wir werden uns zunächst mit der reichhaltigen Klasse von Martingalen beschäftigen und die
wichtigen Martingalkonvergenzsätze kennen lernen. Anschließend konstruieren wir die
Brown’sche Bewegung und studieren ihre Pfadeigenschaften. Infinitesimale Charakteristiken
eines Markov-Prozesses werden durch Generatoren beschrieben, was eine Verbindung zur Theorie
von partiellen Differentialgleichungen ermöglicht. Abschließend kommt mit dem Ergodensatz für
stationäre stochastische Prozesse eine Verallgemeinerung des Gesetzes der großen Zahlen zur
Sprache.
Im Sommersemester 2020 wird diese Voranstaltung durch die Vorlesung Stochastische Analysis
fortgeführt.
Literatur:
-
1.)
- O. Kallenberg: Foundations of Modern Probability (Second Edition), Springer, 2002
-
2.)
- A. Klenke: Wahrscheinlichkeitstheorie (3. Aufl.), Springer Spektrum, 2013
-
3.)
- D. Williams: Probability with Martingales (Cambridge Mathematical Textbooks), Cambridge
University Press, 1991
____________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Folgeveranstaltungen: | Stochastische Analysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Theorie und Numerik partieller
Differentialgleichungen III – Iterative Löser und
Adaptivität |
| | |
Dozent: | Prof. Dr. S. Bartels |
| | |
Zeit/Ort: | Mo, Mi 10–12 Uhr, SR 226, Hermann-Herder-Str. 10 |
| | |
Übungen: | 2-std. n. V. |
| | |
Tutorium: | M.Sc. Christian Palus |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agba/lehre/ |
| | |
| |
_______________________________________________________________
Inhalt:
Sind Lösungen elliptischer partieller Differentialgleichungen nicht H2-regulär, so konvergieren
Finite-Elemente-Methoden auf uniformen Triangulierungen nur mit reduzierter Geschwindigkeit.
In der Vorlesung werden Konzepte diskutiert, um Triangulierungen lokal zu verfeinern und so
eine bessere Auflösung von Eckensingularitäten zu erhalten. Dies kann einerseits auf Basis von
a-priori-Informationen geschehen, das heißt es wird vorab entschieden, wo kleinere Netzweiten
sinnvoll sind, oder es wird mit Hilfe von a-posteriori-Fehlerabschätzungen eine Folge von Gittern
generiert, die kritische Bereiche automatisch identifiziert und entsprechend genauer
auflöst. Neben diesen Aspekten werden iterative Verfahren zur effizienten Lösung der bei
Finite-Elemente-Diskretisierungen auftretenden linearen Gleichungssysteme diskutiert. Unter
Verwendung von Gitterhierarchien oder Gebietszerlegungen lässt sich dies häufig mit nahezu
linearer Komplexität bewältigen.
Literatur:
-
1.)
- S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.
-
2.)
- W. Hackbusch: Iterative Solution of Large Sparse Systems of Equations, Springer, 2016.
_____
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Vorlesung Einführung in Theorie und Numerik partieller
Differentialgleichungen |
Nützliche Vorkenntnisse: | Vorlesungen zu Funktionalanalysis und partiellen
Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Topology of Algebraic Varieties |
| | |
Dozent: | Dr. Bradley Drew und
Prof. Dr. Annette Huber-Klawitter |
| | |
Zeit/Ort: | Di, Do 8–10 Uhr, SR 404, Ernst-Zermelo-Str. 1 |
| | |
Übungen: | n. V. |
| | |
Tutorium: | N.N. |
| | |
| |
_______________________________________________________________
Inhalt:
Complex algebraic varieties are subsets of complex projective space CPn defined by polynomial
equations. These subsets are not manifolds in general, but the types of singularities
that can arise in this algebraic context are not arbitrary. A fundamental problem in
algebraic geometry is therefore to determine which types of singularities may arise
and, more generally, which special topological properties are exhibited by complex
varieties.
In this course, we will study methods first introduced by Solomon Lefschetz to explore
topological properties of complex algebraic varieties. The key idea is to exploit the rigidity of
polynomial equations to reduce questions about varieties in dimension n to questions about
varieties of dimension n - 1. More precisely, Lefschetz pencils allow us to regard a complex
algebraic manifold X of dimension n as a family of complex algebraic varieties Xt, t ∈ CP1, of
dimension n - 1 parametrized by a complex projective line. All but finitely many fibers Xt will
be manifolds. It was Lefschetz’ beautiful insight that knowledge of these fibers and of how
they vary with respect to t determines a great deal of topological data pertaining to
X.
The essential tools to be applied in this course are complex analysis and algebraic topology.
Familiarity with single-variable complex analysis will be assumed. The necessary techniques
from algebraic topology, including singular homology and Poincaré duality, will be
recalled.
Literatur:
-
1.)
- L. Nicolaescu. An invitation to Morse theory. Springer, New York, 2nd ed., 2011.
-
2.)
- K. Lamotke. The topology of complex projective varieties after S. Lefschetz. Topology,
20(1):15–51, 1981.
-
3.)
- A. Hatcher. Algebraic topology. Cambridge University Press, Cambridge, 2002.
-
4.)
- P. Griffiths, J. Harris. Principles of algebraic geometry. John Wiley & Sons, Inc., New York,
1994.
__________________________________________________________________________________________________________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Funktionentheorie |
Nützliche Vorkenntnisse: | kommutative Algebra, Mannigfaltigkeiten oder alg. Topologie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | The course will be held in English |
| |

WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die Aufgabe der Wahrscheinlichkeitstheorie ist es, zufallsabhängige Vorgänge mathematisch
zu beschreiben. Die Vorlesung ist eine systematische Einführung dieses Gebietes auf
maßtheoretischer Grundlage.
Ziel der Vorlesung ist es, Methoden der stochastischen Modellbildung und Analyse zu entwickeln
und einige der klassischen Grenzwertsätze herzuleiten. Vorkenntnisse aus der Vorlesung Analysis
III sind hilfreich, jedoch nicht Voraussetzung.
Literatur:
-
1.)
- Klenke, A.: Wahrscheinlichkeitstheorie (3. Aufl.), Springer Spektrum, 2013
-
2.)
- Kallenberg, O.: Foundations of Modern Probability (Second Edition), Springer, 2002
-
3.)
- Williams, D.: Probability with Martingales, Cambridge University Textbooks, 1991
-
4.)
- Hesse, Ch.: Angewandte Wahrscheinlichkeitstheorie, Springer Vieweg, 2003
______________________
ECTS-Punkte: | 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie II |
Notwendige Vorkenntnisse: | Stochastik |
Nützliche Vorkenntnisse: | Analysis III |
Folgeveranstaltungen: | Stochastische Prozesse (im WS 2020/21); Mathematische
Statistik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Mathematisches Institut
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Vorlesung: | Numerical Optimization |
| | |
Dozent: | Prof. Dr. Moritz Diehl |
| | |
Zeit/Ort: | Online-Kurs in Englisch |
| | |
Übungen: | Di 14–16 Uhr, HS II, Albertstr. 23b |
| | |
Web-Seite: | https://www.syscop.de/teaching/ |
| | |
| |
_______________________________________________________________
Inhalt:
The aim of the course is to give an introduction into numerical methods for the solution of
optimization problems in science and engineering. The focus is on continuous nonlinear
optimization in finite dimensions, covering both convex and nonconvex problems. The
course is accompanied by intensive computer exercises and divided into four major
parts:
-
1.
- Fundamental Concepts of Optimization : Definitions, Types, Convexity, Duality
-
2.
- Unconstrained Optimization and Newton Type Algorithms : Stability of Solutions,
Gradient and Conjugate Gradient, Exact Newton, QuasiNewton, BFGS and Limited
Memory BFGS, and GaussNewton, Line Search and Trust Region Methods,
Algorithmic Differentiation
-
3.
- Equality Constrained Optimization Algorithms : Newton Lagrange and Generalized
Gauss–Newton, Range and Null Space Methods, QuasiNewton and Adjoint Based
Inexact Newton Methods
-
4.
- Inequality Constrained Optimization Algorithms : KarushKuhnTucker Conditions,
Linear and Quadratic Programming, Active Set Methods, Interior Point Methods,
Sequential Quadratic and Convex Programming, Quadratic and Nonlinear
Parametric Optimization
Please read up on the website of the department and/or HISinOne for further information.
The lecture is accompanied by intensive weekly computer exercises based on MATLAB
(6 ECTS) and an optional project (3 ECTS). The project consists in the formulation and
implementation of a self-chosen optimal control problem and numerical solution method,
resulting in documented computer code, a project report, and a public presentation.
Literatur:
-
1.)
- Manuscript Numerical Optimal Control by M. Diehl and S. Gros
-
2.)
- Biegler, L. T., Nonlinear Programming, SIAM, 2010
-
3.)
- Betts, J., Practical Methods for Optimal Control and Estimation Using Nonlinear
Programming, SIAM, 2010
________________________________________________________________________________________
ECTS-Punkte: | nur Vorlesung & Übungen: 6 Punkte; mit Projekt: 9 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Analysis I+II, Lineare Algebra I+II |
Nützliche Vorkenntnisse: | Einführung in
die Numerik, Gewöhnliche Differentialgleichungen, Numerical
Optimization |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Diese Veranstaltung findet als Online-Kurs in englischer
Sprache statt. |
| |
Abteilung für
Quantitative Finanzmarktforschung
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
This course covers an introduction to financial markets and products. Besides futures and
standard put and call options of European and American type we also discuss interest-rate
sensitive instruments such as swaps.
For the valuation of financial derivatives we first introduce financial models in discrete time as
the Cox-Ross-Rubinstein model and explain basic principles of risk-neutral valuation. Finally, we
will discuss the famous Black-Scholes model which represents a continuous time model for option
pricing.
The course, which is taught in English, is offered for the first year in the Finance profile of the
M.Sc. Economics program as well as for students of M.Sc. and B.Sc. Mathematics and
M.Sc. Volkswirtschaftslehre.
For students who are currently in the B.Sc. Mathematics program, but plan to continue with the
special profile Finanzmathematik within the M.Sc. Mathematics, it is recommended to credit
this course for the latter profile and not for B.Sc. Mathematics.
Literatur:
-
1.)
- Chance, D.M., Brooks, R.: An Introduction to Derivatives and Risk Management, (8nd
ed.), South-Western, 2009
-
2.)
- Hull, J.C.: Options, Futures, and other Derivatives (7th ed.), Prentice Hall, 2009
-
3.)
- Shreve, S.E.: Stochastic Calculus for Finance I: The Binomial Asset Pricing Model, Springer
Finance, 2005
-
4.)
- Strong, R.A.: Derivatives. An Introduction, (2nd ed.), South-Western, 2004
____________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Angewandte Mathematik; Kategorie III
Kann für die Spezialisierung Finanzmathematik
im Master-Studiengang auch als wirtschaftswissenschaftliches
Spezialisierungsmodul zählen. |
Nützliche Vorkenntnisse: | Wahrscheinlichkeitstheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Diese zweistündige Vorlesung ist eine Einführung in den Riccifluss. Der Riccifluss ist ein
geometrischer Fluss Riemannscher Mannigfaltigkeiten. Ein geometrischer Fluss deformiert ein
gegebenes geometrisches Objekt durch einen geometrisch definierten Prozess. Dieser Prozess wird
durch eine nichtlineare partielle Differentialgleichung beschrieben. Dadurch entsteht ein reiches
Zusammenspiel zwischen Analysis und Geometrie.
Der Riccifluss ist dabei einer der am meisten untersuchten geometrischen Flüsse. Er ist ein
nützliches und vielseitiges Werkzeug in der Riemannschen Geometrie und geometrischen
Topologie. Besonders hervorzuheben ist Perelmans Lösung der Poincaré-Vermutung mithilfe des
Ricciflusses.
In dieser Vorlesung soll insbesondere behandelt werden:
1) Die Definition des Ricciflusses und die Entwicklung geometrischer Größen
2) Konvergenz Riemannscher Mannigfaltigkeiten und Ricciflüssen
3) Uniformisierung von Flächen: Langzeitexistenz und Konvergenz des Ricciflusses
auf
Flächen
Voraussetzung für das Verständnis der Vorlesung ist eine Vertrautheit mit differenzierbaren
Mannigfaltigkeiten. Wünschenswert sind außerdem einige Kenntnisse der Grundlagen der
Riemannschen Geometrie. Ergänzend zu dieser Vorlesung kann das Seminar über PDE belegt
werden.
Literatur:
-
1.)
- B. Chow, D. Knopf, The Ricci Flow: An Introduction. AMS, 2004
-
2.)
- P. M. Topping, Lectures on the Ricci flow. Cambridge University Press, 2006
____________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Notwendige Vorkenntnisse: | Differentialgeometrie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Depending on the audience the course may be taught in
English or German. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Eine topologische Gruppe ist zugleich eine Gruppe und ein topologischer Raum. Man fordert,
dass die Gruppenstruktur stetig bezüglich der Topologie ist. In der Algebra lernt man, dass man
endliche Gruppen klassifizieren kann, indem man sie als Erweiterung
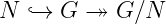
schreibt, wobei N ein Normalteiler und G∕N der entsprechende Quotient ist. Dies reduziert
(mehr oder weniger) die Klassifikation auf die endlichen einfachen Gruppen, also jene, wo keine
weitere solche Zerlegung mehr möglich ist.
Bei topologischen Gruppen geht man ganz analog vor. Nur diesmal sind unsere Gruppen meist
ganz und gar nicht endlich, und statt beliebiger Normalteiler muss man sich auf abgeschlossene
Normalteiler einschränken, damit auch der Quotient G∕N wieder eine vernünftige Topologie
trägt. Ein Beispiel: Man beweist, dass die Zusammenhangskomponente des neutralen Elements
der Gruppe, genannt G0, immer ein abgeschlossener Normalteiler sein muss. Man erhält daher
immer eine Zerlegung
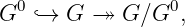
wobei G0 eine zusammenhängende Gruppe ist und G∕G0 eine “total unzusammenhängende” Gruppe.
Daher könnte man sich für eine weitere Klassifikation auf diese zwei Arten von topologischen
Gruppen einschränken.
Allerdings wird jede beliebige Gruppe, wenn man sie mit der diskreten Topologie versieht,
eine topologische Gruppe, d.h. manchmal führt eine solche Reduktion nur auf ein
Klassifikationsproblem, was bekanntermaßen hoffnunglos ist.
Wie Gromov schon sagte: Jede Aussage, die für alle abzählbaren Gruppen gilt, ist entweder
trivial oder falsch.
Die Vorlesung beginnt erst in der zweiten Vorlesungswoche._______________________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Reine Mathematik |
Notwendige Vorkenntnisse: | Grundvorlesungen |
Nützliche Vorkenntnisse: | Topologie, Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
The course is primarily an introduction to infinitary combinatorics, one of the main tools in set
theory and forcing method. More specifically during the course the following topics are
introduced and analysed: Mad families, Martin’s axiom and its equivalent statements, Suslin
problem, infinite trees, club filter, Diamond principles.
Moreover we are going to also give applications of this tools in measure theory and topology. The
course is not meant to include an introduction to forcing method, but it provides a detailed
study of the combinatorics machinery used in forcing theory, in order to give a robust basis for
further studies in that direction as well.
Literatur:
-
1.)
- T. Bartoszynski, H. Judah: Set Theory: On the Structure of the Real Line. AK Peters/CRC
Press, Boca Raton, 1995.
-
2.)
- K. Kunen: Set Theory: An introduction to independence proofs. North Holland, 1983.
_________
ECTS-Punkte: | 6 Punkte |
Verwendbarkeit: | Reine Mathematik; Kategorie III |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
2. Berufsorientierte Veranstaltungen
Mathematisches Institut
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Veranstaltung: | Lernen durch Lehren |
| | |
Dozent: | Alle Dozentinnen und Dozenten von Vorlesungen |
| | |
Zeit/Ort: | Termin und Ort der Einführungsveranstaltung wird
kurzfristig im Vorlesungsverzeichnis in HISinOne bekannt
gegeben |
| | |
| |
_______________________________________________________________
Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu
Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem
Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor
mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um
eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige
oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an
die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im
Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich
(im Zwei-Hauptfächer-Bachelor: „Optionsbereich“) angerechnet. Es handelt sich um eine
Studienleistung, d.h. das Modul wird nicht benotet.
Leistungsnachweis:
- Teilnahme an dem neu konzipierten Einführungsworkshop. Voraussichtlich etwa zwei
halbe Tage; einen ungefähr in der ersten Vorlesungswoche und einen nach etwa vier
Wochen. Näheres wird rechtzeitig bekanntgegeben.
- regelmäßige Teilnahme an der Tutorenbesprechung;
- zwei gegenseitige Tutoratsbesuche
mit einem (oder mehreren) anderen Modulteilnehmer, welcher nach Möglichkeit die
gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten,
und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der
Einführungsveranstaltung).
In Ermangelung eines passenden Wahlbereichs kann das Modul im Lehramtsstudiengang
in dieser Form leider nicht angeboten werden. Im 2-Hauptfächer-Bachelor ist es bei
Wahl der Lehramtsoption eine über die 180 geforderter ECTS-Punkte hinausgehende
Zusatzleistung.__________________________________________________________________________________________________
Abteilung für
Didaktik der Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Didaktische Aspekte beim Einsatz digitaler
Mathematikwerkzeuge im Unterricht |
| | |
Dozent: | Jürgen Kury |
| | |
Zeit/Ort: | Mo 15–18 Uhr, SR 127, Ernst-Zermelo-Str. 1 |
| | |
Übungen: | 1-std. n. V. |
| | |
Tutorium: | Janna Meyer-Boyé |
| | |
Teilnehmerliste: | Interessierte Studierende tragen sich bitte im Didaktik-Sekretariat
bei Frau Schuler (Raum 132, Di–Do, 9–13 Uhr und 14–16:30 Uhr)
ausliegende Liste ein. |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/didaktik/ |
| | |
| |
_______________________________________________________________
Inhalt:
Der Einsatz von Unterrichtsmedien im Mathematikunterricht gewinnt sowohl auf der Ebene der
Unterrichtsplanung wie auch der der Unterrichtsrealisierung an Bedeutung. Vor dem Hintergrund
konstruktivistischer Lerntheorien zeigt sich, dass der reflektierte Einsatz unter anderem von
Computerprogrammen die mathematische Begriffsbildung nachhaltig unterstützen kann. So
erlaubt beispielsweise das Experimentieren mit Computerprogrammen mathematische
Strukturen zu entdecken, ohne dass dies von einzelnen Routineoperationen (wie z. B.
Termumformung) überdeckt würde. Es ergeben sich daraus tiefgreifende Konsequenzen für den
Mathematikunterricht. Von daher setzt sich dieses Seminar zum Ziel, den Studierenden die
notwendigen Entscheidungs- und Handlungskompetenzen zu vermitteln, um zukünftige
Mathematiklehrer auf ihre berufliche Tätigkeit vorzubereiten. Ausgehend von ersten
Überlegungen zur Unterrichtsplanung werden anschließend Computer und Tablets hinsichtlich
ihres jeweiligen didaktischen Potentials untersucht und während eines Unterrichtsbesuchs mit
Lernenden erprobt.
Die dabei exemplarisch vorgestellten Systeme sind:
- dynamische Geometrie Software: Geogebra
- Tabellenkalkulation: Excel
- Apps für Smartphones und Tablets
Die Studierenden sollen Unterrichtssequenzen ausarbeiten, die dann mit Schülern erprobt und
reflektiert werden._____________________________________________________________________________________________
ECTS-Punkte: | 4 Punkte |
Verwendbarkeit: | Modul Fachdidaktische Entwicklung im M.Ed.;
Fachdidaktik-Seminar im Lehramt nach GymPO |
Nützliche Vorkenntnisse: | Grundvorlesungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
In der praktischen Übung zur Numerik-Vorlesung werden die in der Vorlesung entwickelten
und analysierten Algorithmen praktisch umgesetzt und getestet. Dies wird in der
Programmiersprache C++ sowie mit Hilfe der kommerziellen Software MATLAB zur Lösung
und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse
werden vorausgesetzt.
Literatur:
-
1.)
- S. Bartels: Numerik 3x9, Springer Spektrum, 2016.
-
2.)
- P. Deuflhard, A. Hohmann, F. Bornemann: Numerische Mathematik 1, 2 (4./3. Aufl.) De
Gruyter, 2003.
-
3.)
- G. Hämmerlin, K.H. Hoffmann: Numerische Mathematik (4. Aufl.), Springer, 1990.
-
4.)
- R. Plato: Numerische Mathematik kompakt (4. Aufl.), Springer Vieweg, 2010.
-
5.)
- R. Schaback, H. Wendland: Numerische Mathematik (5. Aufl.), Springer, 2005.
-
6.)
- J. Stoer, R. Bulirsch: Numerische Mathematik 1,2 (10./4. Aufl.), Springer 2010/2007.
_______
ECTS-Punkte: | (für Teile 1 und 2 der Praktischen Übung zusammen) 3 Punkte |
Verwendbarkeit: | Pflichtveranstaltung im B.Sc. Mathematik
2-Hf-Bachelor mit Lehramtsoption: Möglicher Teil des
Wahlpflichtmoduls Mathematik
M.Ed.: Möglich als Mathematische Ergänzung (sofern nicht
schon im 2-Hf-Bachelor-Studiengang belegt) |
Notwendige Vorkenntnisse: | Vorlesung Numerik (parallel) |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Die praktische Übung richtet sich an Hörerinnen und Hörer der Vorlesung Stochastik. Es
werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der
Vorlesung vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird
das frei verfügbare Open-Source-Statistikprogramm R verwendet werden. Nach einer
Einführung in R werden u.a. Verfahren der deskriptiven Statistik und graphischen
Auswertung von Daten betrachtet, die numerische Erzeugung von Zufallszahlen erläutert
sowie parametrische und nichtparametrische Tests und lineare Regressionsverfahren
diskutiert. Vorkenntnisse in R und/oder Programmierkenntnisse werden dabei nicht
vorausgesetzt.
Die praktische Übung ist für Studierende im (1-Hauptfach) B.Sc. Mathematik obligatorisch.
Studierende des 2-Hauptfächer-Bachelors mit Lehramtsoption können selbstverständlich
ebenfalls teilnehmen und die praktische Übung als Teil des Wahlpflichtmoduls Mathematik im
Rahmen ihres Studiengangs verbuchen. Im Studiengang Master of Education kann die
Veranstaltung als Mathematische Ergänzung belegt werden.
Für die eigene Arbeit mit R sollen die Laptops der Studierenden eingesetzt werden.
Idealerweise sollte auf diesen bereits vor Beginn der Veranstaltung die dazu notwendige
Software installiert werden. Genauere Anleitungen hierzu sowie entsprechende Links zum
Download der kostenlosen Programme werden frühzeitig auf der o.g. Webseite bekannt
gegeben.
Zu den einzelnen Lektionen der praktischen Übung wird ein ausführliches Skriptum bereitgestellt
werden. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern
möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher
zu R empfohlen werden.______________________________________________________________________________________
ECTS-Punkte: | 3 Punkte |
Verwendbarkeit: | Pflichtveranstaltung im B.Sc. Mathematik
2-Hf-Bachelor mit Lehramtsoption: Möglicher Teil des
Wahlpflichtmoduls Mathematik
M.Ed.: Möglich als Mathematische Ergänzung (sofern nicht
schon im 2-Hf-Bachelor-Studiengang belegt) |
Notwendige Vorkenntnisse: | Analysis I,II, Lineare Algebra I,II, Stochastik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Prakt. Übung zu: | Einführung in Theorie und Numerik partieller
Differentialgleichungen |
| | |
Dozent: | Prof. Dr. M. Růžička |
| | |
Zeit/Ort: | noch nicht bekannt, CIP-Pool, Hermann-Herder-Str. 10 |
| | |
Tutorium: | M.Sc. S. Wolff-Vorbeck |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agru/lehre/index.html |
| | |
| |
_______________________________________________________________
Inhalt:
In den praktischen Übungen sollen die in der Vorlesung „Einführung in die Theorie und Numerik
partieller Differentialgleichungen“ vorgestellten numerischen Verfahren zur Lösung partieller
Differentialgleichungen implementiert werden. Anhand von expliziten Beispielen werden dadurch
in der Vorlesung behandelte, Begriffe (z. B. Konsistenz, Konvergenz, Stabilität, Regularität,...)
veranschaulicht. Ziel ist die Erstellung von Software zur Berechnung von Näherungslösungen
elliptischer Differentialgleichungen mit Hilfe der Finite-Elemente-Methode. Dazu wird die
kommerzielle Software MATLAB zur Lösung und Visualisierung mathematischer Probleme
verwendet.
Elementare Programmierkenntnisse werden vorausgesetzt.
Studierenden, die vorhaben, in der Angewandten Mathematik eine Abschlussarbeit
(Master-oder Bachelorarbeit) zu schreiben, wird die Teilnahme an den praktischen Übungen
empfohlen.
Literatur:
-
1.)
- D. Braess, Finite Elemente, Springer, Berlin (2007)
-
2.)
- H. R. Schwarz, Methode der Finiten Elemente, Teubner, Stuttgart (1991)
-
3.)
- G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010)
-
4.)
- S. Bartels, Numerical Approximation of Partial Differential Equations, Springer (2016)
______
ECTS-Punkte: | 3 Punkte |
Verwendbarkeit: | Wahlmodul im B.Sc. oder M.Sc. Mathematik oder für das
Modul Mathematische Ergänzung im M.Ed. |
Notwendige Vorkenntnisse: | Einführung in Theorie und Numerik partieller
Differentialgleichungen (parallel), Programmierkenntnisse |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Angewandte Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Prakt. Übung zu: | Theorie und
Numerik partieller Differentialgleichungen III –
Iterative Lösung und Adaptivität |
| | |
Dozent: | Prof. Dr. S. Bartels |
| | |
Zeit/Ort: | CIP-Pool Raum 201, Hermann-Herder-Str. 10, 2-std. n. V. |
| | |
Tutorium: | M.Sc. Christian Palus |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agba/lehre/ |
| | |
| |
_______________________________________________________________
Inhalt:
In der praktischen Übung zur Vorlesung sollen die in der Vorlesung entwickelten und
analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der
Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und
Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden
vorausgesetzt.
Literatur:
-
1.)
- S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.
-
2.)
- W. Hackbusch: Iterative Solution of Large Sparse Systems of Equations, Springer, 2016.
_____
ECTS-Punkte: | 3 Punkte |
Verwendbarkeit: | Wahlmodul im B.Sc. oder M.Sc. Mathematik |
Notwendige Vorkenntnisse: | Vorlesung Theorie und Numerik partieller
Differentialgleichungen III (parallel) |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
3. Seminare
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Proseminar: | Darstellungstheorie endlicher Gruppen |
| | |
Dozentin: | Prof. Dr. Annette Huber-Klawitter |
| | |
Zeit/Ort: | Mi 8–10 Uhr, SR 404, Ernst-Zermelo-Str. 1 |
| | |
Tutorium: | N.N. |
| | |
Vorbesprechung: | Do, 18.7.2019, 12:30 Uhr, SR 226,
Hermann-Herder-Str. 10 |
| | |
Teilnehmerliste: | Im Sekretariat bei Frau Frei, R 421. Bei Überbuchung wird ggfs. aus
den Anmeldungen ausgewählt/ausgelost. |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/arithgeom/lehre.html |
| | |
| |
_______________________________________________________________
Inhalt:
Eine Darstellung ist einfach ein Gruppenhomormorphismus von einer Gruppe G in eine
Matrixgruppe Gln(k) für einen Körper k. Die Elemente werden als Matrizen dargestellt.
Wir können nun unser Wissen aus linearer Algebra verwenden, um Aussagen über
Gruppen zu beweisen. Dies ist besonders für endliche Gruppen ein sehr mächtiges
Werkzeug.
Andererseits treten Darstellungen immer dann auf, wenn Vektorräume Symmetrien aufweisen,
z.B. als Lösungsraum einer linearen Differentialgleichung, die gewissen Symmetrien genügt. Oft
ist es nicht leicht, die Lösungsmenge zu bestimmen, aber Darstellungstheorie ermöglicht ein
qualitatives Verständnis. Am bekanntesten ist der Fall der Orbitalmodelle der Elektronen eines
Atoms.
Wir wollen die Grundlagen der Theorie zuerst in dieser konkreten Sprache kennenlernen und
danach in die abstraktere Sprache der Moduln über dem Gruppenring übersetzen. Ein wenig Zeit
für Anwendungen sollte auch sein.
Literatur:
-
1.)
- J.-P. Serre, Linear Representations of Finite Groups, GTM 42, Springer Verlag, 1977
-
2.)
- T.Y. Lam, A first course in noncommutative rings, GTM 131, Second Edition, Springer
Verlag, 2001
_________________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Lineare Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Proseminar: | p-adische Zahlen |
| | |
Dozent: | Prof. Dr. Stefan Kebekus |
| | |
Zeit/Ort: | Mo 10–12, SR 125, Ernst-Zermelo-Str. 1 |
| | |
Tutorium: | Dr. Andreas Demleitner |
| | |
Vorbesprechung: | 24.07.2019, 10.15 Uhr, SR 218, Ernst-Zermelo-Str. 1 |
| | |
Teilnehmerliste: | Eintrag in Liste (im Sekretariat in Raum 421) bis möglichst
15.07.2019 |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/kebekus/ |
| | |
| |
_______________________________________________________________
Inhalt:
Dieses Proseminar verknüpft Analysis und Zahlentheorie. Die Analysis beruht ganz wesentlich
auf dem Begriff der ε-Umgebung – Zahlen sind „nah“, wenn ihre Differenz einen kleinen Betrag
hat. Man kann allerdings auch ganze Zahlen „nah“ nennen, wenn ihre Differenz durch eine hohe
Potenz einer Primzahl p teilbar ist. Ähnlich wie die reellen Zahlen aus den rationalen
entstehen, indem man fordert, dass alle Cauchyfolgen konvergieren sollen, kann man die
rationalen Zahlen auch erweitern, indem man dasselbe für diesen völlig anderen Begriff von
ε-Umgebung fordert. Und genau dies sind die berühmten p-adischen Zahlen. Es gibt
Folgen, die nicht in den reellen Zahlen konvergieren, aber in den p-adischen – und sogar
Folgen, die sowohl p-adisch wie auch reell konvergieren, aber mit unterschiedlichen
Grenzwerten.
Ein Großteil der klassischen Analysis lässt sich auch für die p-adischen Zahlen entwickeln, und
sehr vieles ist ganz ähnlich zur üblichen Analysis, und gleichzeitig doch auch ganz anders. Man
muss sich selbst damit beschäftigen, um diese spannenden Phänomene wirklich verstehen zu
können. Und genau dies wollen wir in diesem Proseminar tun.
Literatur:
-
1.)
- Gouvêa, F.Q.: p-adic Numbers (Second edition), Springer Universitext, 1997
-
2.)
- Jänich, K.: Topologie (8. Aufl.), Springer, 2005
-
3.)
- Katok, S.: p-adic Analysis Compared with Real, AMS, 2007
-
4.)
- Neukirch, J.: Algebraische Zahlentheorie, Springer, 1992
-
5.)
- tom Dieck, T.: Topologie (2. Aufl.), de Gruyter, 2011
-
6.)
- Werner, A.: Nicht-archimedische Zahlen, Vorlesungsskript WS 2012/13, abrufbar unter
http://www.uni-frankfurt.de/50581207/nicht_archi.pdf
________________________________________________
Notwendige Vorkenntnisse: | Analysis I |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
|
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Proseminar: | Einführung in die Variationsrechnung |
| | |
Dozent: | Dr. Susanne Knies |
| | |
Zeit/Ort: | Do 14–16 Uhr, SR 125, Ernst-Zermelo-Str. 1 |
| | |
Tutorium: | M.Sc. Alex Kaltenbach |
| | |
Vorbesprechung: | Mi, 17.07.2019, 13 Uhr, SR 125, Ernst-Zermelo-Str. 1 |
| | |
Teilnehmerliste: | Bitte tragen Sie sich bis zum 12.07.2019 in die Liste ein, die in
Raum 149, Ernst-Zermelo-Str. 1, ausliegt. |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/knies/lehre/ws1920/varia/index.html |
| | |
| |
_______________________________________________________________
Inhalt:
Das Ziel der Variationsrechnung ist es, optimale Lösungen eines Problems zu finden und ihre
Eigenschaften zu beschreiben. Beispiele sind hier die kürzeste Verbindung zweier Punkte, die
größte von einem Rand fester Länge eingeschlossene Fläche oder die Form einer hängenden
Kette.
Aus der Analysis ist die Frage nach dem Auffinden von Minima reeller Funktionen bekannt.
Diese wird in der Variationsrechnung auf das Finden von Minima von Funktionalen
verallgemeinert. Funktionale ordnen einer Funktion u = u(x),x ∈ (a,b), eine reelle Zahl
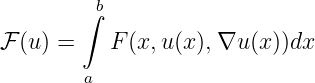 zu.
Hierbei ist die Funktion F gegeben und vom konkreten Problem abhängig. Wir werden
notwendige und hinreichende Bedingungen für Minima des Funktionals
zu.
Hierbei ist die Funktion F gegeben und vom konkreten Problem abhängig. Wir werden
notwendige und hinreichende Bedingungen für Minima des Funktionals 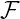 herleiten. Die dafür
notwendigen Hilfsmittel werden im Seminar eingeführt, detailliert behandelt und an Beispielen
illustriert.
herleiten. Die dafür
notwendigen Hilfsmittel werden im Seminar eingeführt, detailliert behandelt und an Beispielen
illustriert.
Eines ersten Eindruck über die Variationsrechnung kann man in der Einleitung von 1.)
gewinnen.
Literatur:
-
1.)
- Hansjörg Kielhöfer, Variationsrechnung, Vieweg + Teubner, 2010 (als elektronischer Volltext
in der UB verfügbar)
_____________________________________________________________________________________________
Notwendige Vorkenntnisse: | Analysis I, II |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Dieses Seminar ist insbesondere auch für Studierende des
2-Hf-Bachelor-Studienganges geeignet. |
| |

Abteilung für
Angewandte Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Ausgewählte Themen der Theorie und Numerik
partieller Differentialgleichungen |
| | |
Dozent: | Prof. Dr. Sören Bartels |
| | |
Zeit/Ort: | Mo 14–16 Uhr, SR 226, Hermann-Herder-Str. 10 |
| | |
Tutorium: | M.Sc. Zhangxian Wang |
| | |
Vorbesprechung: | Mo, 22.7.2019, 15:00 Uhr, SR 226, Hermann-Herder-Str.
10 |
| | |
Teilnehmerliste: | Anmeldung per E-Mail an den Dozenten oder persönlich in der
Sprechstunde |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agba/lehre/ |
| | |
| |
_______________________________________________________________
Inhalt:
Im Seminar sollen verschiedene Aspekte der Finite-Elemente-Methode zur Approximation
elliptischer partieller Differentialgleichungen genauer betrachtet werden. Beispiele dafür sind ein
konstruktiver Beweis des Bramble-Hilbert Lemmas, die Rolle von Winkelbedingungen in
Interpolationsabschätzungen, die Verwendung von Methoden höherer Ordnung und
isoparametrischer Ansätze.
Die Seminarthemen sind auch für Lehramtsstudierende, die an der Vorlesung Einführung in
Theorie und Numerik partieller Differentialgleichungen teilgenommen haben, geeignet.
Literatur:
-
1.)
- D. Braess: Finite Elemente, Springer, 2013.
-
2.)
- S.C. Brenner, L.R. Scott: The Mathematical Theory of Finite Element Methods, Springer,
2007.
-
3.)
- A. Ern, J.-L. Guermond: Theory and Practice of Finite Elements, Springer, 2004.
-
4.)
- P.G. Ciarlet: The Finite Element Method for Elliptic Problems, SIAM, 2002.
_________________________________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Vorlesung Einführung in Theorie und Numerik partieller
Differentialgleichungen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Funktionentheorie |
| | |
Dozentin: | Prof. Dr. Sebastian Goette |
| | |
Zeit/Ort: | Di 14–16, SR 127, Ernst-Zermelo-Str. 1 |
| | |
Tutorium: | Dr. Ksenia Fedosova |
| | |
Vorbesprechung: | Mo, 15.7.2019, 13:00, SR 125, Ernst-Zermelo-Str. 1 |
| | |
Teilnehmerliste: | Eintragung bei Frau Keim, Raum 341, Ernst-Zermelo-Str. 1,
Mo–Fr 9:00–12:00, bis 15.7.2019 |
| | |
Web-Seite: | http://home.mathematik.uni-freiburg.de/goette/ |
| | |
| |
_______________________________________________________________
Inhalt:
Das Seminar umfasst mehrere kleinere Blöcke aus je zwei oder drei Vorträgen mit Ergänzungen
zur Vorlesung „Funktionentheorie“. Zum einen behandeln wir weitere spezielle Funktionen
mit besonderen Eigenschaften. Zum anderen betrachten wir „Riemannsche Flächen“,
das sind Flächen, die lokal wie Teilmengen der komplexen Zahlen aussehen, und auf
denen sich manche holomorphen Funktionen besonders gut beschreiben lassen. Zu
elliptischen Funktionen und zu Polylogarithmen gehören auch spezielle Riemannsche
Flächen. Auch Anwendungen in anderen Teilen der Mathematik sollen nicht zu kurz
kommen.
Geplant sind unter anderem folgende Themen.
- Riemannsche Flächen
- Elliptische Integrale, elliptische Funktionen und die zugehörigen „elliptischen
Kurven“
- Polylogarithmen und ihre Funktionalgleichungen
Literatur wird in der Vorbesprechung angegeben._____________________________________________________
Notwendige Vorkenntnisse: | Vorlesung Funktionentheorie |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Dieses Seminar eignet sich auch für Lehramts- und
M.Ed.-Studierende |
| |

Abteilung für
Angewandte Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Theorie und Numerik für nichtlineare partielle
Differentialgleichungen |
| | |
Dozent: | Prof. Dr. Dietmar Kröner |
| | |
Zeit/Ort: | Di 16–18, SR 226, Hermann-Herder-Str. 10 |
| | |
Tutorium: | M.Sc. Janick Gerstenberger |
| | |
Vorbesprechung: | Mi, 24.07.2019, 14 Uhr, SR 226, Hermann-Herder-Str. 10 |
| | |
Web-Seite: | https://aam.uni-freiburg.de/agkr/lehre/index.html |
| | |
| |
_______________________________________________________________
Inhalt:
In diesem Seminar sollen neueste Arbeiten zur Nicht-Eindeutigkeit von Entropielösungen
für nichtlineare Erhaltungsgleichungen in mehreren Raumdimensionen besprochen
werden.
Literatur:
-
1.)
- E. Chiodaroli: A counterexample to well-posedeness of entropy solutions to the compressible
Euler system, J. Hyperbol. Differ. Eq. 11, 493–519 (2014).
-
2.)
- E. Chiodaroli, L. Gosse: A Numerical Glimpse at Some Non-Standard Solutions to
Compressible Euler Equations, In: Gosse L., Natalini R. (eds) Innovative Algorithms and
Analysis. Springer INdAM Series, Vol. 16, Springer, Cham 2017.
-
3.)
- V. Elling: A possible counterexample to wellposedeness of entropy solutions and to Godunov
scheme convergence, Math. Comp. 75, 1721–1733 (2006).
-
4.)
- S. Marktfelder, C. Klingenberg: The Riemann problem for the multidimensional isentropic
system of gas dynamics is ill-posed if it contains a shock, Arch. Ration. Mech. Anal. 227,
No. 3, 967–994 (2018).
___________________________________________________________________________________________
Notwendige Vorkenntnisse: | Theorie und Numerik partieller Differentialgleichungen,
Hyperbolische Erhaltungssätze |
Nützliche Vorkenntnisse: | Numerik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Integrability is a feature of certain physical models which simplifies calculations, as it allows one
to compute quantities not just approximately and numerically, but exactly and analytically. It
can be understood as the absence of chaotic motion, or more precisely, as a hidden
enhancement of symmetries which substantially constrain the motion. The first examples of
systems that could be solved exactly appeared in classical mechanics: planetary motion,
spinning tops, or harmonic oscillators. A common property of these systems is that
they can be solved by computing the integral of a known function (hence the name
“integrable systems”). In the 19th century, Liouville provided a theoretical framework to
characterise such systems, but the real revolution in the field took place in the 20th century,
when truly general mathematical structures emerged. More recently, the extension of
these results to quantum mechanics, classical and quantum field theories, statistical
mechanics, and string theory led to many important results and is still a very active field of
research.
In this seminar we investigate the mathematical structures that underlie integrable systems. We
focus on the interplay between the group theoretical aspects embodied by the Lax pairs of
operators and the geometric ones represented by certain Riemann surfaces called spectral curves.
Using examples from classical mechanics, we see how the problem of solving equations of motion
transforms into a problem in group theory, how dynamical variables can be expressed in terms of
theta functions associated to the spectral curve, and develop a dictionary between
the two approaches. On the way, we shall learn some useful tools from symplectic
geometry, Riemann surfaces, and Lie and Poisson algebras (no previous knowledge
required!).
Literatur:
-
1.)
- O. Babelon, D. Bernard, M. Talon: Introduction to Classical Integrable Systems, Cambridge
University Press, 2003
____________________________________________________________________________________________
Nützliche Vorkenntnisse: | Funktionentheorie, Differentialgeometrie I |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
Bemerkung: | Die Vorträge können auf Deutsch oder auf Englisch präsentiert
werden. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Das Hauptthema des Seminars ist die elliptische Differentialgleichung
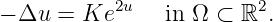
Im Unterschied zur Poissongleichung -Δu = f hängt die rechte Seite von der Lösung u ab, und
zwar exponentiell. Hieraus ergeben sich interessante Fragen zur Existenz, Eindeutigkeit und
Regularität von Lösungen. Die Gleichung wurde zuerst von Liouville im Zusammenhang mit
winkeltreuen Parametrisierungen von Flächen gefunden. Sie spielt eine wesentliche Rolle bei der
Klassifikation geschlossener Flächen nach Poincaré.
Das Seminar wendet sich an Studierende ab dem 5. Semester. Aus den Vorträgen kann eine
Bachelorarbeit entstehen. Vorkenntnisse zur Lösung der Poissongleichung, etwa mit
L2-Theorie, werden vorausgesetzt. Die Literatur zum Seminar wird in der Vorbesprechung
vorgestellt.
Es werden noch Teilnehmer gesucht.______________________________________________________
Notwendige Vorkenntnisse: | Funktionalanalysis |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Deterministische und stochastische Integrationstheorie sind Kernbestandteil moderner Analysis
und bilden die Grundlage für die Lösungstheorie von Differentialgleichungen, mit zahlreichen
Anwendungen in der mathematischen Modellierung. Das Seminar bietet einen Überblick über
verschiedene Konstruktionen von Integralen (Lebesgue, Bochner, Dunford, Pettis, Dobrakov,
Emery, Bichteler, radonifizierend, zylindrisch, …) in der vereinheitlichenden Sprache von
Vektormaßen. Die Theorie liefert Integral-Ungleichungen, aus denen a-priori-Abschätzungen für
Differentialgleichungen gewonnen werden, sowie Integraldarstellungen von bestimmten linearen
Funktionalen. Anwendungen in der Finanzmathematik und darüber hinaus werden je nach
Interesse der Teilnehmer ausgewählt._____________________________________________________________________
Notwendige Vorkenntnisse: | Stochastische Prozesse |
Nützliche Vorkenntnisse: | Stochastische Integration und Finanzmathematik |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Abteilung für
Mathematische Logik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Zahlen |
| | |
Dozent: | PD Dr. Markus Junker |
| | |
Zeit/Ort: | Blockseminar am Ende der Vorlesungszeit |
| | |
Tutorium: | Dr. Daniel Palacin |
| | |
Vorbesprechung: | Fr, 19. 7. 2019, 12:00 Uhr, SR 403, Ernst-Zermelo-Str. 1 |
| | |
Teilnehmerliste: | Bei Interesse bitte Voranmeldung bis 11.7.2019 per Mail an den
Dozenten markus.junker@math.uni-freiburg.de unter Angabe
von Studiengang und Verwendungszweck |
| | |
| |
_______________________________________________________________
Inhalt:
Das Seminar stellt ein Angebot an M.Ed.-Studierende im Praxissemester für das Modul
„Mathematische Ergänzung“ dar, es können aber auch Proseminar-Vorträge und vereinzelte
Vorträge Richtung Mathematische Logik für das Bachelor-Seminar im B.Sc. vergeben werden.
Abschlussarbeiten in einem der Bachelor-Studiengänge oder im M.Ed. können sich
anschließen.
Das Seminar findet als Blockseminar voraussichtlich in der ersten Woche der vorlesungsfreien
Zeit statt. Eventuell beginnen wir mit ersten Vorträgen auch schon im Januar oder Februar; dies
werden wir bei der Vorbesprechung festlegen.
Thema des Seminars ist der Blick auf Zahlbereiche, konkret könnte dies sein:
- Zugänge zu den natürlichen Zahlen: Peano-Arithmetik, Konstruktion aus der
Mengenlehre, Nicht-Standard-Erweiterungen, …
- Konstruktionen der reellen Zahlen aus den rationalen Zahlen
- Verschiedene Zahlbereichserweiterungen über die komplexen Zahlen hinaus
Zum Oberthema passende Themenvorschläge der Teilnehmer sind willkommen.
Bitte melden Sie Ihr Interesse an dem Seminar mit Studiengang und Verwendungswunsch
(Seminar, Proseminar, Bachelor-Seminar) wie oben angegeben an.
Literatur:
-
1.)
- Ebbinghaus et al.: Zahlen, Springer, 1992
-
2.)
- Weitere Literatur je nach konkreten Themen
______________________________________________________________
Verwendbarkeit: | Proseminar
(im B.Sc. Mathematik oder 2-Hf-Bachelor-Studiengang) oder
Seminar im M.Ed. bzw. B.Sc. (auch Bachelor-Seminar) |
Notwendige Vorkenntnisse: | Grundvorlesungen für Proseminarvorträge
Algebra oder Mathematische Logik für Seminarvorträge |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |

Institut für
Medizinische Biometrie und
Statistik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Seminar: | Medical Data Science |
| | |
Dozent: | Prof. Dr. Harald Binder |
| | |
Zeit/Ort: | Mi 10:00–11:30 Uhr, HS Medizinische Biometrie und
Statistik, Stefan-Meier-Str. 26 |
| | |
Vorbesprechung: | Mi, 24.07.2019, 11:30–12:30 Uhr,
Konferenzraum Institut für Medizinische Biometrie und
Statistik, Stefan-Meier-Str. 26, 1. OG |
| | |
Web-Seite: | http://www.imbi.uni-freiburg.de/lehre/WLV/WiSe/Hauptseminar |
| | |
| |
_______________________________________________________________
Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft
ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder
allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data
Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als
Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt
werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue
thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein
oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik
dienen.
Vorherige Anmeldung per E-Mail (sec@imbi.uni-freiburg.de) ist erwünscht._____________
Notwendige Vorkenntnisse: | Gute Kenntnisse in Wahrscheinlichkeitstheorie und
Mathematischer Statistik |
Folgeveranstaltungen: | Kann als Vorbereitung für eine Masterarbeit dienen |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
_______________________________________________________________
______________________________________________________________________
_______________________________________________________________
Inhalt:
Es gibt im Internet eine Reihe interessanter Videos zu mathematischen Themen. Beispielsweise
den YouTube-Kanal Numberphile rund um Brady Haran, aber noch eine Reihe weitere. Dort
wird ganz verschiedenartige Mathematik präsentiert: Etliches kann man vielleicht als
„Unterhaltungsmathematik“ bezeichnen, aber viele Videos greifen auch sehr nichttriviale
Mathematik auf und bemühen sich, sie einem größerem Publikum verständlich zu erklären – also
insbesondere einem Publikum, was nicht gerade das Wissen aus mehreren Semestern
Mathematikstudium zur Hand hat.
Aber das ist bei uns ja anders. Wir kennen ein bisschen mehr Mathematik und wir können uns
die Themen, die hinter so manchen Videos stecken, auch etwas genauer anschauen.
Der Plan des Seminars ist daher, zu einzelnen Videos ein wenig die “Hintergrundstory” zu
erkunden.
Als Beispiel: Die Fibonacci-Folge ist in der Unterhaltungsmathematik sehr bekannt. Aus Sicht
der Zahlentheorie ist sie ein Spezialfall einer linear rekurrenten Folge. Einige spezielle
Eigenschaften der Fibonacci-Folge folgen direkt aus allgemeiner Theorie, z.B. weil die
dominante charakteristische Wurzel der Folge eine sogenannte Pisotzahl ist. Fragen
zu linear rekurrenten Folgen sind auch heute noch ein aktives Forschungsgebiet, so
wurde z.B. die „Pisot Wurzelvermutung“ erst im Jahr 2000 bewiesen (Zannier, Ann. of
Math.).____________________________________________________________________________________________________________
Notwendige Vorkenntnisse: | Funktionentheorie oder Algebra |
Studien-/Prüfungsleistung: | Die Anforderungen an Studien- und Prüfungsleistungen
entnehmen Sie bitte dem aktuellen Modulhandbuch. |
| |
4. Oberseminare, Projektseminare
und Kolloquien
Mathematisches Institut
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Lesekurs: | „Wissenschaftliches Arbeiten“ |
| | |
Dozent: | Alle Dozentinnen und Dozenten des Mathematischen
Instituts |
| | |
Zeit/Ort: | nach Vereinbarung |
| | |
| |
_______________________________________________________________
Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen
Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen
einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im
Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit
einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der
Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da
der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann (im M.Sc. wie im
M.Ed.).
Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen
(typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums,
eventuell Vorträge in einer Arbeitsgruppe, einem Oberseminar, Projektseminar …) werden zu
Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung
sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.
Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung
bestanden ist oder nicht. Im M.Ed. und im Modul „Mathematik“ des M.Sc. gibt es eine
mündliche Abschlussprüfung über den Stoff des Lesekurses, im Vertiefungsmodul des M.Sc. eine
mündliche Abschlussprüfung über sämtliche Teile des Moduls. Ein Lesekurs zur Vorbereitung auf
die Master-Arbeit kann im M.Sc. auch im Wahlmodul angerechnet werden (ohne Prüfung, nur
Studieneistung).
________________________________________________________________________
Notwendige Vorkenntnisse: | hängen vom einzelnen Lesekurs ab |
| |
Abteilung für
Reine Mathematik
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Projektseminar: | Seminar des Graduiertenkollegs GK 1821 |
| | |
Dozent: | Die Dozenten des Graduiertenkollegs |
| | |
Zeit/Ort: | Mi 14–16 Uhr, SR 404, Ernst-Zermelo-Str. 1 |
| | |
Web-Seite: | https://www.gk1821.uni-freiburg.de/ |
| | |
| |
_______________________________________________________________
Inhalt:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in
Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology
or mathematical physics or a mix thereof.
The precise topic will be chosen at the end of the preceeding semester. The program will be
made available via our web site.
The level is aimed at our doctoral students. Master students are very welcome to participate as
well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. A.
Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________
ECTS-Punkte: | im M.Sc.-Studiengang 6 Punkte |
Notwendige Vorkenntnisse: | je nach Thema, meist algebraische Geometrie |
| |
WS2019/20
 ______________________________________________________________________
______________________________________________________________________
Veranstaltung: | Kolloquium der Mathematik |
| | |
Dozent: | Alle Dozenten der Mathematik |
| | |
Zeit/Ort: | Do 17:00 Uhr, HS II, Albertstr. 23 b |
| | |
| |
_______________________________________________________________
Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des
gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet
sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.
Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag
um 17:00 Uhr im Hörsaal II in der Albertstraße 23 b statt.
Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Ernst-Zermelo-Straße 1 den
wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.
Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/


 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
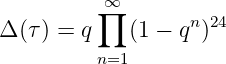
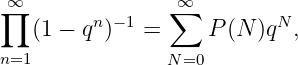

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
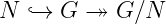
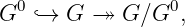
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
![]()
 ______________________________________________________________________
______________________________________________________________________

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
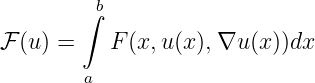
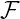
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
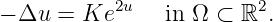

 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________