Lehrveranstaltungen

Inhalt:
Die Vorlesung Analysis III beschäftigt sich mit der Maß- und Integrationstheorie unter besonderer Berücksichtigung des Lebesgue-Maßes. Diese Theorien sind von besonderer Bedeutung für viele weiterführende Vorlesungen aus der Analysis, Angewandten Mathematik, Stochastik, Wahrscheinlichkeitstheorie und Geometrie, sowie der Physik. Schwerpunktthemen sind Maße und Integrale im ℝⁿ, Lebesgueräume, Konvergenzsätze, der Transformationssatz, Oberflächenintegrale und der Integralsatz von Gauss._______________________________________________

Inhalt:
In der linearen Algebra ging es um das Lösen von linearen Gleichungssystemen. Gegenstand der Vorlesung „Algebra und Zahlentheorie“ ist das Lösen von Polynomgleichungen in einer Variablen. Aus der Schule bekannt ist der Fall quadratischer Gleichungen und ihrer Lösungsformel. Eines unserer Hauptresultate wird es sein, dass sich diese Lösungsformel nicht verallgemeinern lässt. Verwandt ist die Frage nach der Konstruierbarkeit mit Zirkel und Lineal.

Unser wesentliches Hilfsmittel ist die Theorie der algebraischen Körpererweiterungen mit dem Hauptsatz der Galoistheorie als Höhepunkt. Auf dem Weg werden wir auch andere algebraische Strukturen wie Gruppen und Ringe studieren.

Von besonderem Interesse ist der Fall von Gleichungen über den rationalen oder gar ganzen Zahlen. Dies ist Gegenstand der Zahlentheorie.

Literatur:

1.)

S. Bosch, Algebra

2.)

S. Lang, Algebra

3.)

F. Lorenz, Algebra 1

4.)

E. Artin, Galois theory

5.)

Van der Waerden, Algebra 1

Inhalt:
Diese Vorlesung ist eine Fortsetzung der Vorlesung Stochastik. Nach einer kurzen Wiederholung von maßtheoretischen Grundlagen werden schwerpunktmäßig Themen wie das Gesetz der großen Zahlen, der zentrale Grenzwertsatz und bedingte Erwartungen behandelt.

Die Vorlesung ist obligatorisch für Studierende, die in Stochastik oder Statistik eine Arbeit schreiben oder einen Prüfungsschwerpunkt wählen wollen.

Literatur:

1.)

Kallenberg, O.: Foundations of Modern Probability, Springer, 2002

2.)

Klenke, A.: Wahrscheinlichkeitstheorie, Springer, 2006

3.)

Williams, D.: Probability with Martingales, Cambridge Mathematical Textbooks, 1991

Inhalt:
Die allgemeine Relativitätstheorie (ART) soll die Wechselwirkung von Materie mit Raum und Zeit beschreiben und erweitert das Gravitationsgesetz von Newton und die spezielle Relativitätstheorie. Sie wurde 1915 von Einstein entwickelt und fasst Gravitation als geometrische Eigenschaft einer vierdimensionalen Mannigfaltigkeit – der Raumzeit – auf.

Über den Weg der speziellen Relativitätstheorie werden wir uns mit den Einsteingleichungen befassen. Wir werden einige spezielle Lösungen kennenlernen – dazu gehören auch schwarze Löcher. Wir werden sowohl geometrische als auch analytische Eigenschaften dieser Lösungen untersuchen.

Des Weiteren werden wir die mathematische Beschreibung hinter einigen wichtiger Tests der ART kennenlernen – von der Lichtablenkung, über die Periheldrehung zu den Gravitationswellen.

In der zweiten Hälfte der Vorlesung wollen wir uns vermehrt analytischen Problemen für Lorentzmannigfaltigkeiten stellen, wie Cauchy-Entwicklungen, Horizonten und Singularitäten.

Literatur:

1.)

R. M. Wald, General Relativity, Chicago Press, 1984

2.)

B. O’Neill, Semi-Riemannian Geometry With Applications to Relativity, Academic Press, 1983

3.)

S. W. Hawking und G. F. R. Ellis, The large scale structure of space-time, Cambridge Monographs, 1973

Inhalt:
 
Den Körper ℝ der reellen Zahlen bekommen wir als Vervollständigung von ℚ bezüglich dem Standardabsolutbetrag, indem wir für jede Cauchy-Folge ihren Limes hinzufügen. Für eine Primzahl p definieren wir den p-adischen Absolutbetrag einer rationalen Zahl q ungleich Null als

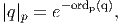
wobei ord_p(q) = n, falls q = pⁿ ⋅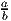, so dass p weder a noch b teilt. Der p-adische Absolutbetrag erfüllt eine starkere Form der Dreiecksungleichung und jede ganze Zahl hat p-adischen Absolutbetrag höchstens 1. Die Vervollständigung von ℚ bezüglich |⋅|_p ist der Körper ℚ_p der p-adischen Zahlen. Somit bekommen wir, unter anderem, ein Element in ℚ_p als Limes der partiellen Reihen

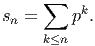
In dieser Vorlesung werden wir Eigenschaften des p-adischen Absolutbetrages und dessen Bewertung ord_p untersuchen. Das Ziel der Vorlesung ist es, eine Vermutung von Emil Artin (fast) positiv zu beantworten: Artin behauptete, dass jedes nicht-triviales Polynom über ℚ_p vom Grad d in mehr als d² + 1 vielen Variablen eine nicht-triviale Nullstelle besitzt.

Literatur:

1.)

Valued Fields, von A. Engler und A. Prestel, Springer Monographs in Mathematics, 2005, ISBN 978-3-540-30035-9

2.)

Local Fields, von P. L. Clark, http://math.uga.edu/~pete/local.pdf

3.)

Valuation Theory, von F. V. Kuhlmann,  https://math.usask.ca/~fvk/Fvkbook.htm

Inhalt:
Die Differentialgeometrie beschreibt und untersucht die geometrischen Eigenschaften gekrümmter Räume mit Methoden der Differentialrechnung. Daher findet die Differentialgeometrie Anwendungen in anderen Bereichen der Mathematik und in der Physik, etwa in der theoretischen Mechanik und der Relativitätstheorie.

In der Vorlesung werden zunächst die grundlegenden Begriffe und Methoden der Differentialgeometrie eingeführt (wie differenzierbare Mannigfaltigkeiten, Vektorbündel und Tensorfelder). Darauf aufbauend wird eine Einführung in die Riemannsche Geometrie gegeben, die ein Teilgebiet der Differentialgeometrie ist. Hier werden insbesondere Geodätische und der Riemannsche Krümmungstensor im Mittelpunkt stehen. Dort, wo es wenig Mehraufwand bedeutet, werden auch die etwas allgemeineren Strukturen der semi-Riemannschen Geometrie eingeführt, da diese grundlegend in der Relativitätstheorie benötigt werden. Sofern die Zeit es erlaubt, werden im letzten Teil der Vorlesung Aspekte der speziellen Relativitätstheorie vorgestellt.

Literatur:

1.)

Barrett O’Neill, Semi-Riemannian Geometry with Applications to Relativity, Academic Press, 1983

2.)

J.M. Lee, Introduction to Smooth Manifolds, Springer (GTM 218), 2003

3.)

M.P. do Carmo, Riemannian Geometry, Birkhäuser, 1992

4.)

jedes andere Buch zur Differentialgeometrie

Inhalt:
Die Holonomie einer dimensionalen Riemannschen Mannigfaltigkeit gibt Auskunft über zusätzliche parallele geometrische Strukturen.

In der Vorlesung behandeln wir zunächst Kähler-Mannigfaltigkeiten; diese tragen eine parallele komplexe Struktur. Typische Beispiele sind glatte komplexe algebraische Varietäten, und die Kählergeometrie stellt einen Zusammenhang zwischen Differential- und algebraischer Geometrie her. Ein Spezialfall sind Calabi-Yau-Mannigfaltigkeiten, die unter anderem für die Physik von Interesse sind.

Als nächstes betrachten wir symmetrische Räume. Ihre Geometrie lässt sich vollständig durch die Wirkung ihrer Isometriegruppe beschreiben. Einfache Beispiele sind die Modellräume konstanter Krümmung, projektive Räume und Grassmann-Mannigfaltigkeiten.

Die Sätze von de Rham und Berger beschreiben alle möglichen Holonomiegruppen. Manche spezielle Holonomiegruppen führen dazu, dass die Ricci-Krümmung verschwindet, und alle bekannten Beispiele kompakter Mannigfaltigkeiten mit Ricci-Krümmung 0 haben spezielle Holonomie.

Zum Schluss betrachten wir 7-dimensionale Mannigfaltigkeiten mit Holonomie G₂, die ebenfalls von physikalischem Interesse sind. Wir interessieren uns für geometrische Eigenschaften und konstruieren einzelne Beispiele.

Literatur:

1.)

W. Ballmann, Lectures on Kähler manifolds, ESI Lect. Math. Phys., EMS, Zürich, 2006, x+172 pp

2.)

A. L. Besse, Einstein manifolds, Springer-Verlag, Berlin, 1987, xii+510 pp

3.)

D. Joyce, Compact manifolds with special holonomy, Oxford University Press, Oxford, 2000, xii+436 pp

Inhalt:
Die Vorlesung beschäftigt sich mit der numerischen Approximation von Lösungen linearer partieller Differentialgleichungen. Der Schwerpunkt liegt dabei auf der Behandlung des Poisson-Problems mit der Methode der Finiten Elemente. Diese Differentialgleichung beschreibt stationäre Wärmeverteilungen und Diffusionsprozesse und ist wesentlicher Bestandteil vieler mathematischer Beschreibungen realer Vorgänge. Die numerische Lösung basiert auf einer Variationsformulierung und einer Zerlegung des physikalischen Gebiets in Dreiecke oder Tetraeder. Damit wird ein kontinuierliches, unendlich-dimensionales Problem durch ein endlich-dimensionales lineares Gleichungssystem approximiert, welches effizient am Rechner gelöst werden kann. Die Exaktheit der Approximation in Abhängigkeit der analytischen Eigenschaften der kontinuierlichen Lösung und die iterative Lösung des linearen Gleichungssystems sind Schwerpunkte der Vorlesung. Im begleitenden Praktikum werden die theoretischen Ergebnisse experimentell verifiziert.

Die Vorlesung ist so konzipiert, dass auch Lehramtsstudenten, die die Vorlesung Mehrfachintegrale gehört haben, daran teilnehmen können.

Literatur:

1.)

S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.

2.)

D. Braess: Finite Elemente. Springer, 2007.

3.)

S. Brenner, R. Scott: Finite Elements. Springer, 2008.

4.)

M. Dobrowolski: Angewandte Funktionalanalysis. Springer, 2005.

5.)

L. C. Evans: Partial Differential Equations. AMS, 2010.

6.)

B. Schweizer: Partielle Differentialgleichungen. Springer, 2013.

Inhalt:
Wir betrachten geometrische Variationsprobleme mit kritischer Skalierung, unter anderem harmonische Abbildungen und Flächen vorgeschriebener mittlerer Krümmung, eventuell auch Willmoreflächen. Es sollen Resultate zur Regularität von Wente, Hélein und Rivière vorgestellt werden. Es handelt sich um Grenzfälle, bei denen die Standardmethoden nicht ausreichen, sondern es muss aus der geometrischen Struktur eine Zusatzinformation abgeleitet und analytisch umgesetzt werden. Siehe http://home.mathematik.uni-freiburg.de/analysis/GeomAnalysisWS1819/GV_2015.pdf

Literatur:

1.)

F. Hélein: Harmonic Maps, Conservation Laws and Moving Frames (second edition), Cambridge University Press 2002.

2.)

T. Lamm: Geometric Variational Problems, Vorlesung FU Berlin, 2007.

Inhalt:
Die Statistik beschäftigt sich mit Methoden und Verfahren zur Analyse empirischer Daten. Das Ziel der Mathematischen Statistik ist es, derartige Methoden und Verfahren aus der Statistik mathematisch – insbesondere mit Mitteln der Wahrscheinlichkeitstheorie – zu untersuchen, und allgemeingültige Aussagen über sie zu beweisen. Für die Vorlesung sind unter anderem folgende Themen vorgesehen:

• Statistische Modelle, suffiziente Statistiken, exponentielle Familien
• Schätzmethoden, Momentenmethode, Maximum-Likelihood-Schätzung
• Vergleich von Schätzern, Informationsungleichung, asymptotische Theorie
• Konfidenzintervalle, Hypothesentests, Neyman-Pearson Lemma
• Nichtparametrische Modelle, Satz von Glivenko-Cantelli, Anpassungstests
• Lineare Modelle, Satz von Gauß-Markov

Literatur:

1.)

C. Czado, T. Schmidt: Mathematische Statistik. Springer, 2011

2.)

H.-O. Georgii: Einführung in die Wahrscheinlichkeitstheorie und Statistik. De Gruyter, 2015

3.)

U. Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik. Vieweg, 2005

4.)

H. Pruscha: Vorlesungen über Mathematische Statistik. Springer Vieweg, 2000

Inhalt:
Die Modelltheorie untersucht den Zusammenhang zwischen mathematischer Syntax und Semantik, d. h. zwischen der Art, wie mathematische (hier vor allem: algebraische) Eigenschaften in formaler Sprache ausgedrückt werden, und dem Verhalten ihrer Modelle.

Ein offensichtliches Beispiel eines solchen Zusammenhangs liefert die Beobachtung, dass universelle (d. h. durch Allquantoren ausdrückbare) Eigenschaften von Strukturen auf ihre Unterstrukturen übergehen. Es gilt aber auch die Umkehrung: Unter Unterstrukturen abgeschlossene Modellklassen sind durch universelle Eigenschaften axiomatisierbar.

Die Vorlesung soll bis zu den Sätzen von Morley und Baldwin-Lachlan kommen, die eine Strukturtheorie für sogenannte ℵ₁-kategorische Theorien entwickeln, die die aus der Linearen Algebra bekannte Dimensionstheorie von Vektorräumen verallgemeinert: K-Vektorräume sind bis auf Isomorphie durch ihre Dimension charakterisiert, Ein anderes Beispiel sind algebraisch abgeschlossene Körper fester Charakteristik, die bis auf Isomorphie durch ihren Transzendenzgrad bestimmt sind.

Die Vorlesung setzt einige Kenntnisse aus der formalen Logik voraus, die zu Beginn rasch wiederholt werden. Sie kann ohne vorausgehende „Mathematische Logik“ gehört werden, wenn man bereit ist, sich diese Logik-Grundlagen im Selbststudium anzueignen. Beispiele kommen meistens aus der Algebra und setzen vereinzelt algebraische Kenntnisse voraus.

Literatur:

1.)

M. Ziegler: Skript „Modelltheorie“, 2001. home.mathematik.uni-freiburg.de/ziegler/skripte/

2.)

K. Tent, M. Ziegler: “A course in model theory”, Association of Symbolic Logic 2012.

3.)

W. Hodges: “Model Theory”, Cambridge University Press 1993

Inhalt:
Die Vorlesung „Stochastische Prozesse“ schließt direkt an die „Wahrscheinlichkeitstheorie“ aus dem vergangenen WS 2017/18 an. Ausgehend von den dort behandelten bedingten Erwartungen werden zunächst Martingale in diskreter Zeit eingeführt und die klassischen Martingalkonvergenzsätze behandelt. Anschließend erfolgt der Übergang zu zeitstetigen Prozessen (X_t)_t≥0, die Familien von überabzählbar vielen Zufallsvariablen sind. Neben etwas allgemeiner Theorie werden hierbei insbesondere die Brownsche Bewegung und allgemeiner auch Lévy-Prozesse genauer besprochen und der Zusammenhang mit unbegrenzt teilbaren Verteilungen und dem allgemeinen zentralen Grenzwertsatz beleuchtet. Wenn Zeit bleibt, soll auch noch kurz auf den Satz von Donsker und dessen Anwendungen eingegangen werden.

Die Vorlesung ist der erste Teil des Stochastik-Zyklus innerhalb des Master-Studiengangs Mathematik und damit grundlegend für alle Studierenden, die in diesem Bereich ihren Schwerpunkt legen und eine Abschlussarbeit schreiben möchten, insbesondere für diejenigen, die eine Spezialisierung innerhalb der Profillinie Finanzmathematik anstreben.

Literatur:

1.)

Kallenberg, O.: Foundations of Modern Probability, Springer, 2002

2.)

Klenke, A.: Wahrscheinlichkeitstheorie, 3. Aufl., Springer Spektrum, 2013

3.)

Rüschendorf, L.: Wahrscheinlichkeitstheorie, Springer Spektrum, 2016

4.)

Sato, K.-I.: Lévy Processes and Infinitely Divisible Distributions, Cambridge University Press, 1999

Inhalt:
In der Vorlesung werden numerische Verfahren zur approximativen Lösung zeitabhängiger und nichtlinearer partieller Differentialgleichungen untersucht. Insbesondere werden typische Beispiele nicht-konvexer Variationsprobleme, nicht-glatter Optimierungsprobleme, singular gestörter parabolischer Gleichungen und Probleme mit nicht-linearen Nebenbedingungen diskutiert. Die Verfahren basieren meist auf Finite-Elemente-Diskretisierungen im Ort und Differenzenquotienten zur Approximation von Zeitableitungen bei Gradientenflüssen. Im Rahmen der Übungen werden neben theoretischen Aufgaben einfache MATLAB-Programme für die Realisierung der Methoden modifiziert.

Literatur:

1.)

S. Bartels: Numerical Methods for Nonlinear Partial Differential Equations, Springer, 2015.

2.)

S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.

3.)

L. C. Evans: Partial Differential Equations. AMS, 2010.

4.)

H. W. Alt: Lineare Funktionalanalysis. Springer, 2006.

5.)

M. Dobrowolski: Angewandte Funktionalanalysis. Springer, 2005.

6.)

B. Schweizer: Partielle Differentialgleichungen. Springer, 2013.

Inhalt:
Zu Beginn der Vorlesung steht eine kurze Vorstellung der gängigsten Axiomensysteme der Mathematik: ZFC und NBG. Die Axiome prägen unsere Auffassung von den möglichen definierbaren oder vielleicht weniger konstruktiv gegebenen mathematischen Objekten. Allerdings zeichnen sie kein vollständiges Bild eines einzigen mathematischen Universums. Die Liste der herleitbaren mathematischen Aussagen ist unvollständig: Für manche φ ist weder φ noch sein Negat aus den Zermelo-Fraenkel’schen Axiomen ZFC beweisbar. Man sagt „φ ist unabhängig von ZFC“.

Die bekannteste von ZFC unabhängige Aussage ist die Kontinuumshypothese, die sagt, dass es genau ℵ₁ reelle Zahlen gibt.

Die Vorlesung führt in die Technik der Unabhängigkeitsbeweise ein. Nach ersten einfachen Forcings zur Kardinalzahlexponentiation werden wir ZF-Modelle ohne AC und iterierte Forcings (z.B. zum Nachweis der relativen Konsistenz von Martins Axiom) kennenlernen. Es gibt ein Skript aus früheren Jahren.

Literatur:

1.)

H.-D. Ebbinghaus, Einführung in die Mengenlehre. 4. Auflage, 2003.

2.)

Paul Eklof, Alan Mekler, Almost Free Modules, Revised Edition, North-Holland, 2002.

3.)

Lorenz Halbeisen, Combinatorial Set Theory. With a Gentle Introduction to Forcing, Springer, 2012.

4.)

Thomas Jech, Set Theory. The Third Millenium Edition, Springer, 2001.

5.)

Kenneth Kunen, Set Theory, An Introduction to Independence Proofs, North-Holland, 1980.

6.)

Kenneth Kunen, Set Theory. Second Edition, College Publications, 2013.

7.)

Saharon Shelah, Proper and Improper Forcing, Springer, 1998.

Inhalt:

Das Ziel der Variationsrechnung ist, gewisse mathematisch fassbare Größen zu minimieren oder zu maximieren. Genauer gesagt betrachten wir auf Ω ⊂ ℝⁿ Funktionale bzw. Variationsintegrale der Form

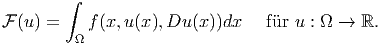
Beispiele sind Bogenlänge und Flächeninhalt, sowie Energien von Feldern in der Physik. Die zentrale Fragestellung ist die Existenz von Minimierern. Nach einer kurzen Vorstellung der funktionalanalytischen Hilfsmittel werden wir zunächst einige notwendige und hinreichende Bedingungen für die Existenz von Minimierer kennenlernen. Wir werden sehen, dass Kompaktheit dabei eine ausgesprochen wichtige Rolle spielt. Anschließend werden wir einige Techniken vorstellen, die uns in Spezialfällen helfen, auch ohne Kompaktheit auszukommen: Die sogenannte kompensierte Kompaktheit und die konzentrierte Kompaktheit.

Literatur:

1.)

M. Struwe, Variational methods. Applications to nonlinear partial differential equations and Hamiltonian systems. Fourth edition. A Series of Modern Surveys in Mathematics, 34. Springer-Verlag, Berlin, 2008.

2.)

J.Jost, X.Li-Jost,Calculus of Variations, Cambridge Univ.Press, 1999

Inhalt:
The course’s aim is to give an introduction into numerical methods for the solution of optimization problems in science and engineering. The focus is on continuous nonlinear optimization in finite dimensions, covering both convex and nonconvex problems. The course is accompanied by intensive computer exercises and divided into four major parts:

1.

Fundamental Concepts of Optimization : Definitions, Types, Convexity, Duality

2.

Unconstrained Optimization and Newton Type Algorithms : Stability of Solutions, Gradient and Conjugate Gradient, Exact Newton, QuasiNewton, BFGS and Limited Memory BFGS, and GaussNewton, Line Search and Trust Region Methods, Algorithmic Differentiation

3.

Equality Constrained Optimization Algorithms : Newton Lagrange and Generalized Gauss–Newton, Range and Null Space Methods, QuasiNewton and Adjoint Based Inexact Newton Methods

4.

Inequality Constrained Optimization Algorithms : KarushKuhnTucker Conditions, Linear and Quadratic Programming, Active Set Methods, Interior Point Methods, Sequential Quadratic and Convex Programming, Quadratic and Nonlinear Parametric Optimization

Bitte informieren Sie sich auf der Webseite des Lehrstuhls oder in HISinOne über weitere Angaben.

Umfang:
Der Kurs besteht aus Vorlesung mit Übungen und 6 ECTS-Punkte; er kann wahlweise durch ein zusätzliches Projekt auf 9 ECTS-Punkte aufgestockt werden._____________________________________

Inhalt:
Wir behandeln die Theorie gewöhnlicher Differentialgleichungen. Solche Gleichungen bilden die Grundlage vieler mathematischer Modelle in Physik, Biologie und in den Wirtschaftswissenschaften. Ferner sind sie in vielen weiterführenden mathematischen Vorlesungen relevant, z.B. in der Differentialgeometrie. In dieser Vorlesung werden folgende Themen behandelt:

1.

Elementare Lösungsmethoden: Trennung der Variablen und Variation der Konstanten.

2.

Existenz- und Eindeutigkeitssätze für Anfangswertprobleme: Satz von Picard-Lindelöf, Lemma von Gronwall, differenzierbare Abhängigkeit von Daten.

3.

Lineare Systeme: Fundamentalsystem, Evolutionsoperator.

4.

Wir werden versuchen, stets auch Anwendungsbeispiele aus den Naturwissenschaften zu untersuchen.

Literatur:

1.)

Walter, Gewöhnliche Differentialgleichungen, Springer 7. Aufl., 2000.

2.)

Heuser, Gewöhnliche Differentialgleichungen, Vieweg und Teubner 6. Aufl., 2009.

3.)

Amann, Gewöhnliche Differentialgleichungen, DeGruyter 2. Aufl., 2011.

Inhalt:
This course covers an introduction to financial markets and products. Besides futures and standard put and call options of European and American type we also discuss interest-rate sensitive instruments such as swaps.

For the valuation of financial derivatives we first introduce financial models in discrete time as the Cox–Ross–Rubinstein model and explain basic principles of risk-neutral valuation. Finally, we will discuss the famous Black–Scholes model which represents a continuous time model for option pricing.

In addition to the lecture there will be general tutorial. We also recommend to visit the seminar Bootstrapping and Derivative Pricing in R where the theoretical methods taught in the lecture will be practically implemented and applied to real data problems.

The course, which is taught in English, is offered for the first year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. and B.Sc. Mathematics and M.Sc. Volkswirtschaftslehre.

For students who are currently in the B.Sc. Mathematics program, but plan to continue with the special profile Finanzmathematik within the M.Sc. Mathematics, it is recommended to credit this course for the latter profile and not for B.Sc. Mathematics.

Literatur:

1.)

Chance, D.M., Brooks, R.: An Introduction to Derivatives and Risk Management, (8th ed.), South-Western, 2009

2.)

Hull, J.C.: Options, Futures, and other Derivatives (7th ed.), Prentice Hall, 2009

3.)

Shreve, S.E.: Stochastic Calculus for Finance I: The Binomial Asset Pricing Model, Springer Finance, 2005

4.)

Strong, R.A.: Derivatives. An Introduction, (2nd ed.), South-Western, 2004

Inhalt:
Die Versicherungsmathematik hat sich zu einem unverzichtbaren Werkzeug für Versicherungsunternehmen entwickelt. Sie beschäftigt sich mit der mathematischen Modellierung sowie der statistischen Schätzung von versicherten Risiken (insbesondere Schäden an Personen oder Sachen), der Kalkulation des benötigten Preises für die Übernahme solcher Risiken, und der Berechnung von versicherungstechnischen Rückstellungen oder der benötigten Eigenmittelausstattung. Die Versicherungsmathematik gehört zur angewandten Mathematik und stellt ein wesentliches Anwendungsgebiet der Wahrscheinlichkeitstheorie und der Mathematischen Statistik dar. In der Vorlesung werden unter anderem folgende Themen behandelt:

• Lebensversicherungsmathematik, Barwerte, Zahlungsströme, Deckungskapital, Modellierung mit Markov-Ketten
• Schadenversicherungsmathematik, individuelles Modell, kollektives Modell, Schadenverteilungen, Panjer-Klasse
• Ruintheorie, Cramér-Lundberg Modell, Poisson-Prozess, Prämienkalkulation

Die Übungsblätter werden voraussichtlich in englischer Sprache erscheinen. Die Vorlesung ist auf Deutsch vorgesehen, kann bei Interesse aber auch auf Englisch gehalten werden.

Literatur:

1.)

S. Asmussen, H. Albrecher: Ruin Probabilities. World Scientific, 2010

2.)

P. Embrechts, C. Klüppelberg, T. Mikosch: Modelling Extremal Events. Springer, 1997

3.)

M. Koller: Stochastische Modelle in der Lebensversicherung. Springer, 2010

4.)

H. Milbrodt, M. Helbig: Mathematische Methoden in der Personenversicherung. De Gruyter, 1999

5.)

K.D. Schmidt: Versicherungsmathematik. Springer, 2006

Inhalt:
Die Theorie der Riemannschen Flächen spielt eine spezielle Rolle in der Mathematik und liegt in der Überschneidung der Topologie, der Analysis, der algebraischen Geometrie, der Riemannschen Geometrie und der mathematischen Physik. Riemannsche Flächen sind historisch entstanden als der natürliche Definitionsbereich zunächst mehrdeutiger Funktionen wie etwa des Logarithmus oder der Wurzelfunktion. Das Ziel dieser Vorlesungsreihe ist es, eine Einführung in dieses vielfältige und schöne Gebiet der Mathematik zu liefern.

Literatur:

1.)

Donaldson. Riemann surfaces.

2.)

Farkas, Kra. Riemann surfaces.

3.)

Freitag. Funktionentheorie 2.

4.)

Kirwan. Complex algebraic curves.

Inhalt:
The idea is to introduce a notion of intersection of two closed subvarieties of a smooth variety. We start with the intersection multiplicity of two plane projective curves and discuss a number of application of the same.

We then introduce the Chow groups of a variety and study the intersection product using the Chern classes of a vector bundle and deformation of the normal cone. The techniques and concepts used in this process have their own importance. Using intersection products, we prove that the direct sum of the Chow groups of a smooth variety is actually a ring, called the Chow ring (or intersection ring) of the variety. If time permits, we also prove Grothendieck-Riemann-Roch Theorem, which relates the Chow ring with K₀, the Grothendieck group of vector bundles on the smooth variety.

Literatur:

1.)

W. Fulton: Algebaic curves, An introduction to algebraic geometry

2.)

W. Fulton: Intersection theory (second edition)

3.)

D. Eisenbud and J. Harris: 3264 and all that

Inhalt:
Lie-Algebren beschreiben „infinitesimale Symmetrie“ und ihre Theorie ist mit den Mitteln der Grundvorlesungen zur linearen Algebra gut zugänglich. Die Motivation kommt jedoch aus der Differentialgeometrie und Physik.

In dieser Vorlesung soll die Theorie der halbeinfachen Lie-Algebren im Mittelpunkt stehen. Sie bildet einen guten ersten Einstieg in viele Gebiete der Mathematik, an denen aktuell intensiv geforscht wird.__________________________________________________________________________________________________

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich (im Zwei-Hauptfächer-Bachelor: „Optionsbereich“) angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Leistungsnachweis:

• Teilnahme am Workshop „Fit für das Tutorat“ – Teilnahme nur nach Rücksprache mit der Dozentin, Frau Lickert – ersatzweise kann ein Erfahrungsbericht über das Tutorat geschrieben werden;
• Teilnahme an der Einführungsveranstaltung (zu Vorlesungsbeginn; Termin wird kurzfristig im Vorlesungsverzeichnis bekanntgegeben);
• regelmäßige Teilnahme an der Tutorenbesprechung;
• zwei gegenseitige Tutoratsbesuche mit einem anderen Modulteilnehmer, welcher nach Möglichkeit die gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der Einführungsveranstaltung).

In Ermangelung eines passenden Wahlbereichs kann das Modul im Lehramtsstudiengang in dieser Form leider nicht angeboten werden. Im 2-Hauptfächer-Bachelor ist es bei Wahl der Lehramtsoption eine über die 180 geforderter ECTS-Punkte hinausgehende Zusatzleistung.__________________________________________________________________________________________________

Inhalt:
Aufgaben spielen im Mathematikunterricht eine zentrale Rolle, sei es als Anlass zum Entdecken mathematischer Zusammenhänge, zum Üben von Fertigkeiten, zum Vernetzen von Begriffen oder als Instrument zur Leistungsbewertung. Zwar gibt es Aufgabensammlungen, jedoch bleibt die individuelle Erarbeitung guter Aufgaben eine zentrale Tätigkeit der Lehrenden. Jede Lehrerin und jeder Lehrer benötigt deswegen Handwerkszeug, um für die vielfältigen Gelegenheiten und Zwecke eigene Aufgaben zu erstellen oder um vorliegende Aufgaben zielgerichtet zu verändern. Hierfür benötigt man Begriffe, mit denen man die Eigenschaften von Aufgaben erfassen kann, sowie Kriterien und Verfahren, nach denen man Aufgaben systematisch erstellen und anpassen kann. Ein Verständnis für guten Unterricht bildet dabei die Grundlage für die Aufgabenkonstruktion.

Im Seminar werden Kriterien für geeignete Aufgaben vermittelt und konkrete Techniken der zielgerichteten Aufgabenentwicklung erarbeitet und geübt. Dabei dient die Konstruktion der Aufgaben auch der Reflexion über die eigenen pädagogischen Absichten und fachlichen Ziele.

Literatur:

1.)

Büchter, A. & Leuders, T. (2014). Mathematikaufgaben selbst entwickeln. Lernen fördern – Leistung überprüfen. Cornelsen, Berlin.

Inhalt:
In der praktischen Übung zur Numerikvorlesung werden die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet. Dies wird in der Programmiersprache C++ sowie mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

1) Zum Wintersemester 2018/19 wird der Master-of-Education-Studiengang eingeführt.

In Mathematik sind die folgenden fachwissenschaftlichen Module zu absolvieren: „Erweiterung der Analysis“ (Pflichtveranstaltung, angeboten jedes WS, mit Klausur) „Mathematische Ergänzung“ (z.B. ein Seminar oder eine Praktische Übung, SL) „Mathematische Vertiefung“ (eine vierstündige Vorlesung zur Wahl, mit mündlicher Abschlussprüfung) Im aktuellen Wintersemester kommen in Frage: „Analysis III“; bei Nacharbeiten evtl. fehlender Vorkenntnisse auch „Einführung in Theorie und Numerik partieller Differentialgleichungen“, „Modelltheorie“, „Wahrscheinlichkeitstheorie“. Alternativ zu „Mathematische Vertiefung“ können diejenigen, die eine fachwissenschaftliche Master-Arbeit schreiben wollen, das Modul „Wissenschaftliches Arbeiten“ absolvieren (Selbststudium als Vorbereitung der Master-Arbeit, mit mündlicher Abschlussprüfung)

Außerdem sind die folgenden fachdidaktischen Module bzw. veranstaltungen zu absolvieren: „Didaktik der Funktionen und der Analysis“ (Pflichtveranstaltung, angeboten jedes WS) „Didaktik der Stochastik und der Algebra“ (Pflichtveranstaltung, angeboten jedes SS) Beide zusammen bilden ein Modul mit gemeinsamer Abschlussklausur Für diejenigen, die eine fachdidaktische Master-Arbeit schreiben wollen, das Modul „Fachdidaktische Forschung in der Mathematik“ (begrenzte Teilnehmerzahl, Beginn nach dem Praxissemester, SL) Für die anderen das Modul „Fachdidaktische Entwicklung in der Mathematik“ (verschiedene Veranstaltungen zur Wahl, im aktuellen WS das Fachdidaktikseminar „Mathematikaufgaben entwickeln“, SL)

2) Für die Lehramtsstudiengänge nach GymPO werden verschiedene Veranstaltungen nicht mehr angeboten:

„Mehrfachintegrale“. Ersatz: „Erweiterung der Analysis“ „Elementargeometrie“ als 2+1-stündige Veranstaltung. Ersatz: „Elementargeometrie“ als 2+2-stündige Veranstaltung. Die Vorlesungen „Didaktik der Algebra und Analysis und „Didkatik der Geometrie und Stochastik“. Ersatz, wenn nur eine Vorlesung fehlt: „Einführung in die Fachdidaktik der Mathematik“. Wenn beide Vorlesungen fehlen, zusätzlich „Didaktik der Funktionen und der Analysis“ oder „Didaktik der Stochastik und der Algebra“. Alle für das Modul „Fachdidaktische Entwicklung in der Mathematik“ vorgesehenen Veranstaltungen können als Fachdidaktikseminare absolviert werden.

Die Ersatzveranstaltungen müssen in jedem Fall komplett absolviert werden, auch wenn sie eine mit größerem Arbeitsaufwand (in ECTS-Punkten) versehen sind. liothek mehr !!

Literatur:

1.)

S. Bartels : Numerik 3x9. Springer, 2016.

2.)

R. Plato : Numerische Mathematik kompakt. Vieweg, 2006.

3.)

R. Schaback, H. Wendland : Numerische Mathematik. Springer, 2004.

4.)

J. Stoer, R. Burlisch : Numerische Mathematik I, II. Springer, 2007, 2005.

5.)

G. Hämmerlin, K.-H. Hoffmann : Numerische Mathematik. Springer, 1990.

6.)

P. Deuflhard, A. Hohmann, F. Bornemann : Numerische Mathematik I, II. DeGruyter, 2003.

Inhalt:
Die praktische Übung richtet sich an Hörerinnen und Hörer der Vorlesung Stochastik. Es werden computerbasierte Methoden diskutiert, die das Verständnis des Stoffes der Vorlesung vertiefen und weitere Anwendungsbeispiele aufzeigen sollen. Dazu wird das frei verfügbare Open-Source-Statistikprogramm R verwendet werden. Nach einer Einführung in R werden u.a. Verfahren der deskriptiven Statistik und graphischen Auswertung von Daten betrachtet, die numerische Erzeugung von Zufallszahlen erläutert sowie parametrische und nichtparametrische Tests und lineare Regressionsverfahren diskutiert. Vorkenntnisse in R und/oder Programmierkenntnisse werden dabei nicht vorausgesetzt.

Die praktische Übung ist für Studierende im (1-Hauptfach) B.Sc. Mathematik obligatorisch. Studierende des 2-Hauptfächer-Bachelors mit Lehramtsoption können selbstverständlich ebenfalls teilnehmen und die praktische Übung als Teil des Wahlpflichtmoduls Mathematik im Rahmen ihres Studiengangs verbuchen. Im Studiengang Master of Education kann die Veranstaltung als Mathematische Ergänzung belegt werden.

Für die eigene Arbeit mit R sollen die Laptops der Studierenden eingesetzt werden. Idealerweise sollte auf diesen bereits vor Beginn der Veranstaltung die dazu notwendige Software installiert werden. Genauere Anleitungen hierzu sowie entsprechende Links zum Download der kostenlosen Programme werden frühzeitig auf der o.g. Webseite bekannt gegeben.

Zu den einzelnen Lektionen der praktischen Übung wird ein ausführliches Skriptum bereitgestellt werden. Als ergänzende Lektüre für diejenigen, die ihre R-Kenntnisse festigen und erweitern möchten, kann eigentlich nahezu jedes der inzwischen zahlreich erhältlichen einführenden Bücher zu R empfohlen werden.______________________________________________________________________________________

Inhalt:
In der praktischen Übung zur Vorlesung sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.

Inhalt:
In der praktischen Übung zur Vorlesung sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

S. Bartels: Numerical Approximation of Partial Differential Equations, Springer, 2016.

2.)

S. Bartels: Numerical Methods for Nonlinear Partial Differential Equations, Springer, 2015.

Inhalt:
In diesem Proseminar geht es vor allem um Flächen, wie etwas die Kugel, den Torus oder die Kleinsche Flasche. Es gliedert sich in drei Teile: elementare Topologie, Klassifikation geschlossener Flächen, sowie Fundamentalgruppen.

Im ersten Teil vertiefen wir unsere topologischen Grundbegriffe aus der Analysis. Dabei konzentrieren wir uns auf topologische Mannigfaltigkeiten, wie sie auch in vielen Bereichen der Geometrie und Topologie eine große Rolle spielen. Wir lernen einige wichtige Eigenschaften dieser Räume kennen, und eine Reihe elementarer Konstruktionen.

Im zweiten Teil klassifizieren wir alle kompakten zusammenhängenden Flächen ohne Rand. Wir nehmen dazu nur an, dass die Flächen sich aus Dreiecken zusammensetzen lassen, und zeigen, dass jede Fläche zu einer von zwei abzählbaren Familien gehört, die wir anschaulich konstruieren können.

Im dritten Teil führen wir die Fundamentalgruppe eines topologischen Raumes ein. Wir können die Fundamentalgruppe der kompakten Flächen angeben, und zeigen mit ihrer Hilfe, dass alle oben konstruierten Flächen paarweise nicht homöomorph sind.

Literatur:

1.)

John M. Lee; Introduction to Topological Manifolds, Springer GTM202, 2000

2.)

K. Jänich, Topologie, 7.Auflage, Springer, 2001

Inhalt:
Die Teilnehmer sollen anhand eigener Vorträge die Grundbegriffe der Topologie parallel zur Vorlesung Analysis II vertiefen. Schwerpunkte sind die Konstruktion von topologischen Räumen sowie die Definition und Berechnung der Fundamentalgruppe topologischer Räume.

Das Vortragsprogramm orientiert sich im wesentlichen am Buch von McCleary. Die Bücher von Armstrong und Jänich dienen als weitere Quellen. Das Buch von Jänich mag insbesondere bei der deutschen Terminologie helfen.

Literatur:

1.)

M.A. Armstrong: Basic Topology, Springer

2.)

K. Jänich: Topologie, Springer

3.)

J. McCleary: A First Course in Topology, AMS

Inhalt:
Es sollen Konzepte zur Beschreibung der Geometrie von Fraktalen eingeführt werden, etwa Dimension oder Selbstähnlichkeit. Es handelt sich vor allem um Begriffe der Geometrischen Maßtheorie. Die benötigten Grundlagen zur Maßtheorie werden mit behandelt, sie sind nicht Voraussetzung des Proseminars. Grundlage des Proseminars ist das Buch von Falconer, das auch viele Beispiele enthält.

Literatur:

1.)

K. Falconer: Fractal Geometry (Mathematical Foundations and Applications), John Wiley & Sons, Chichester 1990.

Inhalt:
Im Proseminar werden einige schöne Resultate aus der Analysis mit elementaren Mitteln bewiesen.

Literatur:

1.)

Naas, Tutschke: Große Sätze und schöne Beweise der Mathematik, Verlag Harry Deutsch (1997).

2.)

Aigner, Ziegler: Das Buch der Beweise, Springer (2015)

Inhalt:
 
In vielen Modellen zur Beschreibung von Vorgängen in den Naturwissenschaften treten gewöhnliche Differentialgleichungen auf. In diesem Seminar werden wir uns sowohl mit der Herleitung dieser Gleichungen als auch Herleitung und Visualisierung expliziter Lösungen beschäftigen.

Evt. wird das Seminar mit 2 Terminen pro Woche in der ersten Hälfte des WS stattfinden.

Literatur:

1.)

R. Borrelli, C. Coleman, Differential Equations: a modeling perspective, Wiley, 2004

2.)

Ch. Constanda, Differential Equations, Springer, 2017

Inhalt:
Das Seminar soll in die Theorie endlicher und affiner Spiegelungsgruppen einführen. Eine Spiegelungsgruppe ist eine Gruppe von Bewegungen eines euklidischen Raumes, die durch Spiegelungen erzeugt wird.

Wir werden unter anderem die endlichen Spiegelungsgruppen klassifizieren, eine Darstellung durch Erzeugende und Relationen herleiten, und die Ringe der invarianten Polynomfunktionen studieren.

Literatur:

1.)

James E. Humphreys: Finite reflection groups

2.)

N. Bourbaki: Lie 4–6

3.)

W. Soergel: Skript “Spiegelungsgruppen und Wurzelsysteme”

Inhalt:
A lattice Γ of rank n in ℝⁿ is an additive subgroup of ℝⁿ of the form Γ = ℤe ₁ ⊕… ⊕ ℤe_n where is a basis of ℝⁿ. An example of a lattice in ℝⁿ is ℤⁿ ⊂ ℝⁿ. An important tool to study lattices, the so-called theta function of a lattice, comes from complex analysis. It is a holomorphic function on the complex upper half plane ℍ and contains information about distributions of lattice points of fixed length. For example, if a lattice Γ is even, which means that the square of the length of x is an even integer for each x ∈ Γ, then the theta function can be used to count the number of lattice points of length 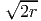for each positive integer r. If an even lattice has the so-called unimodularity property, then the corresponding theta function becomes a modular form, which is a holomorphic function on ℍ with certain symmetry properties. The theory of modular forms is useful in the classification of lattices, for instance, it can be used to show that there is a unique even unimodular lattice of rank 8 in ℝ⁸ up to isomorphism.

The theory of lattices interacts deeply with coding theory. Here, by definition, a code is a certain fixed set whose elements are the “codewords”. Choosing this “dictionary” and its mathematical properties conveniently can enable correction of transmission errors. As such, coding theory has many applications, for example in the telephone and satellite communication. There are some surprising parallels between the theory of lattices and coding theory. For example, the notion of unimodularity in the theory of lattices is analogous to the notion of self duality in coding theory, the theta function in the theory of lattices is analogous to the so-called weight numerator in coding theory and so on.

In this seminar, we will study lattices, codes and modular forms. We will also explore connections between them including the ones mentioned above.

Literatur:

1.)

J. Bruinier, G. van der Geer, G. Harder & D. Zagier, The 1-2-3 of Modular Forms, Springer-Verlag, 2008

2.)

J.H. Conway & N.J.A. Sloane, Sphere Packings, Lattices and Groups, Third edition, Springer-Verlag, 1999

3.)

W. Ebeling, Lattices and Codes, Advanced Lectures in Mathematics, Third edition, Springer Spektrum, 2013

Inhalt:
 
Die geometrische Gruppentheorie ist ein Teilbereich der Mathematik, in dem Gruppen als geometrische Objekte untersucht und Verbindungen zwischen algebraischen Eigenschaften einer Gruppe und geometrischen Eigenschaften eines Raumes, auf welche die Gruppe über Isometrien agiert, erforscht werden.

Hyperbolische Gruppen sind Verallgemeinerungen der fundamentalen Gruppe π₁(X) auf einer Fläche X mit dem Geschlecht g = 2. In diesem Fall untersucht die geometrische Gruppentheorie die Verbindungen zwischen π₁(X) und der hyperbolischen Ebene.

Obgleich die geometrische Gruppentheorie eine relativ neue Disziplin ist, hat sie bereits Anwendungen in vielen anderen Bereichen innerhalb der Mathematik. Es hat sich beispielweise herausgestellt, dass viele tradtionelle algebraische Probleme schnelle und transparente Lösungen für hyperbolische Gruppen besitzen, während sie für Gruppen mit endliche Präsentationen generell unlösbar sind. Eines dieser Probleme ist das folgende: Gegeben ist eine endliche Präsentation einer Gruppe G. Gibt es einen Algorithmus, welcher das Wort w als Eingabe in den Erzeugern annimmt und entscheidet, ob w die Identität von G darstellt oder nicht.

In diesem Seminar studieren wir hyperbolische Gruppen und deren Anwendung. Wir werden die hyperbolische Geometrie diskutieren, Fuchs’sche Gruppen studieren, die Notation eines Cayley Graphen einführen, beweisen, dass der Cayley Graph bestimmter Gruppen quasi-isomorph zur hyperbolischen Ebene ist, das Wort-Problem und Dehns Algorithmus untersuchen und über klassische isoperimetrische Ungleichungen reden.______________________________________________________

Inhalt:
1967 definierte Jerome Keisler eine Präordnung (reflexiv und transitiv) ⊲ auf den abzählbaren vollständigen Theorien mit unendlichen Modellen: T₁ ⊲ T₂ sagt grob, dass fast jede Ultrapotenz von T₁-Modellen einfacher ist als die entsprechende Ultrapotenz von T₂-Modellen. Zur Modelltheorie kommt die Mengenlehre ins Spiel bei der Konstruktion der Ultrafilter. Bis 1972 kannte man etwa drei Bereiche und fünf vage Trennlinien in der Keislerordnung.

Erst um 2010 wurde die Untersuchung der mysteriösen Keisler’schen Präordnung mit kombinatorischen Ergebnissen über Hypergraphen kombiniert, und dadurch wurden Anforderungen an Indikator-Ultrafilter herauskristallisiert.

Im Seminar beginnen wir mit der Keisler’schen Arbeit und den Shelah’schen Arbeiten von 1971 und studieren dann die Umstrukturierungsarbeiten durch Maryanthe Malliaris, die den Weg zum bahnbrechenden Fortschritt durch Malliaris und Shelah ab 2011 bereiteten.

Die untenstehende Liste ist nur eine Auswahl.

Literatur:

1.)

H. Jerome Keisler, Ultraproducts which are not saturated, J. Symbolic Logic 32 (1967), 23–46.

2.)

Saharon Shelah, Saturation of ultrapowers and Keisler’s order, Ann. Math. Logic 4 (1972), 75–114.

3.)

Maryanthe Malliaris, Independence, order, and the interaction of ultrafilters and theories Ann. Pure Appl. Logic 163 no. 11 (2012), 1580–1595.

4.)

Malliaris; Shelah. A dividing line within simple unstable theories. Adv. Math. 249 (2013), 250–288.

5.)

Malliaris; Shelah. Model-theoretic properties of ultrafilters built by independent families of functions. J. Symb. Log. 79 (2014), no. 1, 103–134.

6.)

Malliaris; Shelah. Constructing regular ultrafilters from a model-theoretic point of view. Trans. Amer. Math. Soc. 367 (2015), no. 11, 8139–8173.

7.)

Malliaris; Shelah,. Cofinality spectrum theorems in model theory, set theory, and general topology. J. Amer. Math. Soc. 29 (2016), no. 1, 237–297.

8.)

Malliaris; Shelah. Existence of optimal ultrafilters and the fundamental complexity of simple theories. Adv. Math. 290 (2016), 614—681.

9.)

Malliaris, Maryanthe; Shelah, Saharon; Keisler’s order has infinitely many classes. Israel J. Math. 224 (2018), no. 1, 189–230. __________________________________________________

Notwendige Vorkenntnisse:	Mathematische Logik
Nützliche Vorkenntnisse:	Modelltheorie, Mengenlehre
Studien-/Prüfungsleistung:	Die Anforderungen an Studien- und Prüfungsleistungen entnehmen Sie bitte dem aktuellen Modulhandbuch.

WS2018/19 _________________________________________________________

Seminar/Lesekurs:	Shape Analysis
Dozent:	Philipp Harms
Zeit/Ort:	Mi 14–16 Uhr, Raum 232, Ernst-Zermelo-Str. 1
Vorbesprechung:	Mi, 17.10.2018, 14:15 Uhr, Raum 232, Ernst-Zermelo-Str. 1
Teilnehmerliste:	Um teilzunehmen, kommen Sie bitte in die Vorbesprechung des Seminars; eine Teilnehmerliste wird nicht vorab ausliegen.
Web-Seite:	https://www.stochastik.uni-freiburg.de/lehre/ws-2018-2019/seminar-shapeanalysis-ws-2018-2019/info-seminar-shapeanalysis-ws-2018-2019

_______________________________________________________________

Inhalt:
Shape Analysis beschäftigt sich mit der Modellierung und Analyse von geometrischen Daten. Beispielsweise sind dies Datensätze von Kurven, Flächen und Tensorfeldern aus bildgebenden Verfahren der Medizin, oder Bilddaten mit Tiefeninformation, die von einigen Handykameras bereits mitgeliefert wird. Shape Analysis ist ein interdisziplinäres Forschungsgebiet, welches Methoden und Fragestellungen aus folgenden Gebieten vereint:

• Riemannsche Differentialgeometrie in endlicher und unendlicher Dimension
• Statistik, Stochastik und Machine Learning auf Mannigfaltigkeiten
• Anwendungen in Computational Anatomy, Computergrafik, Anthropologie und weiteren Gebieten mit nichtlinearen hochdimensionalen Daten

Die Themen des Seminars werden je nach Vorwissen und Interesse ausgewählt. Geplant ist eine Einführung in differentialgeometrische Aspekte von Shape Analysis, gefolgt von individuellen Einheiten zu angewandteren Themen.____________________________________________________________________

Notwendige Vorkenntnisse:	Elementare Differentialgeometrie
Studien-/Prüfungsleistung:	Die Anforderungen an Studien- und Prüfungsleistungen entnehmen Sie bitte dem aktuellen Modulhandbuch.

Abteilung für
Reine Mathematik

WS2018/19 _________________________________________________________

Seminar:	Adele
Dozentin:	Annette Huber-Klawitter
Zeit/Ort:	Mo 14–16 Uhr, SR 404, Ernst-Zermelo-Str. 1
Tutorium:	N. N.
Vorbesprechung:	Mo, 16.7.2018, 14 ct, SR 125, Ernst-Zermelo-Str. 1
Teilnehmerliste:	im Sekretariat bei Frau Frei (Raum 421, Ernst-Zermelo-Str. 1)
Web-Seite:	http://www.mathematik.uni-freiburg.de/home/arithgeom

_______________________________________________________________

Inhalt:
Das Zusammenspiel von lokaler und globaler Information ist ein Grundprinzip der Zahlentheorie. Mit lokal meint man hier Information, die nur von einer Primzahl abhängt, beispielsweise die Lösungen einer ganzzahligen Gleichungen modulo p, p² etc. Wir arbeiten dann mit der Komplettierung des Zahlkörpers bezüglich der Bewertung, die zu einem Primideal gehört. Dies reicht nicht: es muss auch die lokale Information “im Unendlichen” berücksichtigt werden – die Information über R oder C. Man beobachtet, dass es sich in beiden Fällen um lokal-kompakte Körper handelt.

Der Ring der Adele eines Zahlkörpers K fasst diese Information sehr elegant zusammen. Man erhält einen lokal-kompakten Ring A_K. Invertierbare Matrizen über A bilden eine lokal-kompakte Gruppe. Solche Gruppen tragen ein kanonisches Maß und sind damit analytischen Methoden wie der Fourier-Theorie zugänglich.

Im Fall der 1x1-Matrizen erhält man die Idele, die eine herausragende Rolle in Klassenkörpertheorie spielen, also der Klassifikation der abelschen Erweiterungen eines Zahlkörpers.

Im Seminar wollen wir die Adele einführen und studieren. Ziel ist die Herleitung der Funktionalgleichung der Riemannschen Zeta-Funktion aus der Fourier-Inversionsformel.

Literatur:

1.)

D. Ramakrishnan, R. Valenza, Fourier analysis on number fields. Graduate Texts in Mathematics, 186. Springer-Verlag, New York, 1999

2.)

Algebraic number theory. Proceedings of an instructional conference organized by the London Mathematical Society (a NATO Advanced Study Institute) with the support of the International Mathematical Union. Edited by J. W. S. Cassels and A. Fröhlich Academic Press, London; Thompson Book Co., Inc., Washington, D.C. 1967

3.)

John Tate, Fourier analysis in number fields and Hecke’s zeta functions, Thesis Princeton 1950.

__________________________________________________________________________________________________________________

Notwendige Vorkenntnisse:	algebraische Zahlentheorie
Nützliche Vorkenntnisse:	Maßtheorie (z.B. Analysis III)
Studien-/Prüfungsleistung:	Die Anforderungen an Studien- und Prüfungsleistungen entnehmen Sie bitte dem aktuellen Modulhandbuch.

Abteilung für
Reine Mathematik

WS2018/19 _________________________________________________________

Seminar:	Minimalflächen
Dozentin:	Prof. Dr. Guofang Wang
Zeit/Ort:	Mi 16–18 Uhr, SR 403, Ernst-Zermelo-Str. 1
Tutorium:	Dr. Azahara de la Torre Pedraza
Vorbesprechung:	Mi, 18.07.2018, 17:00–18:00 Uhr, SR 318, Ernst-Zermelo-Str. 1
Web-Seite:	http://home.mathematik.uni-freiburg.de/wang/

_______________________________________________________________

Inhalt:
 
Minimalflächen sind Flächen im Raum mit „minimalem“ Flächeninhalt und lassen sich mithilfe holomorpher Funktionen beschreiben. Sie treten u.a. bei der Untersuchung von Seifenhäuten und der Konstruktion stabiler Objekte (z.B. in der Architektur) in Erscheinung. Bei der Untersuchung von Minimalflächen kommen elegante Methoden aus verschiedenen mathematischen Gebieten wie der Funktionentheorie, der Variationsrechnung, der Differentialgeometrie und der partiellen Differentialgleichung zur Anwendung.

Das Seminar eigent sich für den Bachelor/Master-Studenten als auch für den Lehramt-Studenten.

Literatur:

1.)

Osserman, R., A survey of minimal surfaces, Van Nostrand 1969.

2.)

J.-H. Eschenburg, J. Jost, Differentialgeometrie und Minimalflächen, Springer 2007.

3.)

Kuwert, Einführung in die Theorie der Minimalflächen, Skript 1998

4.)

W. H. Meeks III, J. Pérez A survey on classical minimal surface theory

5.)

Colding, T., Minicozzi, W. P., Minimal Surfaces, New York University 1999.

_________________________________________________________________________________________________________________________

Notwendige Vorkenntnisse:	Analysis III oder Mehrfachintegrale, und Funktionentheorie
Nützliche Vorkenntnisse:	Elementare Differentialgeometrie

   

Abteilung für
Angewandte Mathematik

WS2018/19 _________________________________________________________

Seminar:	Formoptimierung
Dozent:	Prof. Dr. P. Dondl
Zeit/Ort:	Mo 14–16 Uhr, SR 226, Hermann-Herder-Str. 10
Tutorium:	Wird noch bekannt gegeben
Vorbesprechung:	Do, 02.08.2018, 16 Uhr, Zi. 217, Hermann-Herder-Str. 10
Web-Seite:	http://aam.uni-freiburg.de/agdo/lehre/ws18/shape_opt/

_______________________________________________________________

Inhalt:
Die typische Fragestellung der Formoptimierug ist es, die Form eines Körpers zu finden, welche – unter gewissen Nebenbedingungen – ein Funktional maximiert oder minimiert. Ein Beispiel ist das Finden einer optimalen Form eines elastischen Körpers mit vorgegebenem Volumen, so dass die mechanische Nachgiebigkeit unter einer gegebenen Lastverteilung minimiert wird.

In diesem Seminar betrachten wir sowohl theoretische Fragestellungen, wie zum Beispiel die Wohlgestelltheit des Problems als auch die praktische Umsetzung einer solchen Optimierung. Gefundene optimale Formen können auf einem 3D-Drucker anschließend hergestellt werden.
Bei entsprechender Nachfrage können auch einige für Lehramtsstudierende geeignete Themen vergeben werden.

Literatur:

1.)

M. P. Bendsøe, O. Sigmund. Topology Optimization. Springer 2003.

2.)

G. Allaire. Shape Optimization by the Homogenization Method. Springer 2002.

Weitere Literatur wird noch bekannt gegeben._________________________________________________________________

Nützliche Vorkenntnisse:	Einfürung in die Theorie und Numerik (auch parallel), Funktionalanalysis

Abteilung für
Reine Mathematik

WS2018/19 _________________________________________________________

Seminar:	Algebraische Geometrie
Dozentin:	Prof. Dr. Stefan Kebekus
Zeit/Ort:	Mi 10–12 Uhr, SR 403, Ernst-Zermelo-Straße 1
Tutorium:	J. Commelin
Vorbesprechung:	Fr, 13.07.2018, 13:00 Uhr, SR 218, Ernst-Zermelo-Str. 1
Web-Seite:	https://cplx.vm.uni-freiburg.de

_______________________________________________________________

Inhalt:
Das Thema des Seminares wird komplexe Algebraische Geometrie sein. Das Seminar richtet sich an Studierende, die bereits eine weiterführende Vorlesung in Algebra oder Geometrie gehört haben und sich für eine Abschlussarbeit (BA/MA) interessieren.

Die Themenwahl orientiert sich an den Vorkenntnissen der Teilnehmer. Interessenten werden daher gebeten, sich vorab mit Johann Commelin (Raum 408, Ernst-Zermelo-Str. 1) in Verbindung zu setzen, damit Vorkenntnisse abgeklärt und passende Themen gefunden werden können.___________________________________________________________________________________________________________

Notwendige Vorkenntnisse:	Vorkenntnisse in Algebra, Algebraischer Geometrie, Komplexer Geometrie oder auch Differentialgeometrie, Topologie, Funktionentheorie mehrerer Veränderlicher
Studien-/Prüfungsleistung:	Die Anforderungen an Studien- und Prüfungsleistungen entnehmen Sie bitte dem aktuellen Modulhandbuch.

WS2018/19 _________________________________________________________

Seminar:	Quantitative Versionen des zentralen Grenzwertsatzes
Dozentin:	Prof. Dr. Angelika Rohde
Zeit/Ort:	geplant ist: Mi 14–16 Uhr, SR 127, Ernst-Zermelo-Str. 1
Tutorium:	Pascal Beckedorf
Vorbesprechung:	Do, 19.07.2018, 14:00 Uhr, Raum 232, Ernst-Zermelo-Str. 1
Web-Seite:	https://www.stochastik.uni-freiburg.de/lehre/ws-2018-2019/seminar-quantitative-versionen-des-zentralen-grenzwertsatzes-ws-2018-2019

_______________________________________________________________

Inhalt:
Eines der fundamentalsten Resultate in der Wahrscheinlichkeitstheorie ist der zentrale Grenzwertsatz. Es besagt, dass die Verteilung eines normalisierten Mittels von unabhängigen, identisch verteilten Zufallsvariablen mit endlicher Varianz gegen die Normalverteilung konvergiert. Unter stärkeren Annahmen spezifiziert der Satz von Berry-Esseen sogar die Rate, mit der der Abstand zur Grenzverteilung gegen Null konvergiert.

In diesem Seminar werden wir solche quantitativen Grenzwertsätze wie den Satz von Berry-Esseen unter allgemeineren Abhängigkeitsstrukturen und für komplexe Statistiken studieren. Dabei werden wir insbesondere auf die exakten Abweichungsterme, die mithilfe der sogenannten Edgeworth-Entwicklung bestimmt werden, eingehen können. Für das Seminar relevante aktuelle Artikel werden in der Vorbesprechung vorgestellt.

Aufbauend auf diesem Seminar können Bachelor- und Masterarbeiten vergeben werden.

Literatur:

1.)

V. V. Petrov: Sums of Independent Random Variables, Springer, 1975.

2.)

R. N. Bhattacharya, R. R. Rao: Normal Approximation and Asymptotic Expanisons, Wiley, 1976.

3.)

V. Bentkus, F. Götze: The Berry-Esseen Bound for Students’s Statistic, The Annals of Probability, 1996.

__________________________________________________________________________________________________

Notwendige Vorkenntnisse:	sehr gute Kenntnisse der Wahrscheinlichkeitstheorie
Studien-/Prüfungsleistung:	Die Anforderungen an Studien- und Prüfungsleistungen entnehmen Sie bitte dem aktuellen Modulhandbuch.

Institut für
Medizinische Biometrie und
Statistik

WS2018/19 _________________________________________________________

Seminar:	Medical Data Science
Dozent:	Prof. Dr. Harald Binder
Zeit/Ort:	Mi 10–11:30 Uhr, HS Medizinische Biometrie und Statistik, Stefan-Meier-Str. 26
Web-Seite:	http://portal.uni-freiburg.de/imbi/lehre/WS/Hauptseminar

_______________________________________________________________

Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik dienen.

Vorbesprechung mit Hinweisen auf einführende Literatur:
Mittwoch den 11.07.2018, 10:30–11:30 Uhr, Konferenzraum Institut für Medizinische Biometrie und Statistik, Stefan-Meier-Str. 26, 1. OG

Vorherige Anmeldung per E-Mail (sec@imbi.uni-freiburg.de) ist erwünscht._____________

Notwendige Vorkenntnisse:	gute Kenntnis in Wahrscheinlichkeitstheorie und Mathematischer Statistik
Folgeveranstaltungen:	kann als Vorbereitung für eine Masterarbeit dienen
Studien-/Prüfungsleistung:	Die Anforderungen an Studien- und Prüfungsleistungen entnehmen Sie bitte dem aktuellen Modulhandbuch.

 

4. Oberseminare, Projektseminare

und Kolloquien

Mathematisches Institut

WS2018/19 _________________________________________________________

Lesekurs:	„Wissenschaftliches Arbeiten“
Dozent:	Alle Dozentinnen und Dozenten des Mathematischen Instituts
Zeit/Ort:	nach Vereinbarung

_______________________________________________________________

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann.

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe (einem Oberseminar, Projektseminar …)) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im Vertiefungsmodul gibt es eine mündliche Abschlussprüfung über den Stoff des Lesekurses und den weiteren Stoff des Moduls.____________________________________________

Notwendige Vorkenntnisse:	hängen vom einzelnen Lesekurs ab

Abteilung für
Reine Mathematik

WS2018/19 _________________________________________________________

Projektseminar:	Seminar des Graduiertenkollegs GK 1821
Dozent:	Die Dozenten des Graduiertenkollegs
Zeit/Ort:	Mi 14–16 Uhr, SR 404, Ernst-Zermelo-Str. 1
Web-Seite:	http://gk1821.uni-freiburg.de

_______________________________________________________________

Inhalt:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology or mathematical physics or a mix thereof.

The precise topic will be chosen at the end of the preceeding semester. The program will be made available via our web site.

The level is aimed at our doctoral students. Master students are very welcome to participate as well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. A. Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________

ECTS-Punkte:	im MSc-Studiengang 6 Punkte
Notwendige Vorkenntnisse:	je nach Thema, meist algebraische Geometrie

Abteilung für
Reine Mathematik

WS2018/19 _________________________________________________________

Forschungseminar:	Internationales Forschungsseminar Algebraische Geometrie
Dozent:	Prof. Dr. Stefan Kebekus
Zeit/Ort:	zwei Termine pro Semester, n.V., IRMA – Strasbourg, siehe Website
Web-Seite:	http://home.mathematik.uni-freiburg.de/kebekus/ACG/

_______________________________________________________________

Inhalt:
The Joint Seminar is a research seminar in complex and algebraic geometry, organized by the research groups in Freiburg, Nancy and Strasbourg. The seminar meets roughly twice per semester in Strasbourg, for a full day. There are about four talks per meeting, both by invited guests and by speakers from the organizing universities. We aim to leave ample room for discussions and for a friendly chat.

The talks are open for everyone. Contact one of the organizers if you are interested in attending the meeting. We have some (very limited) funds that might help to support travel for some junior participants.____________________________________________________________________________________________

Mathematisches Institut

WS2018/19 _________________________________________________________

Veranstaltung:	Kolloquium der Mathematik
Dozent:	Alle Dozenten der Mathematik
Zeit/Ort:	Do 17:00 Uhr, HS II, Albertstr. 23 b

_______________________________________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17:00 Uhr im Hörsaal II in der Albertstr. 23 b statt.

Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Eckerstraße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/

 

[next] [prev] [prev-tail] [front] [up]