Lehrveranstaltungen

Inhalt:
Gegenstand der Vorlesung ist die Maß– und Integrationstheorie nach Lebesgue. Es wird ein abstrakter Aufbau der Maßtheorie vorgestellt, der in etwa dem Buch von Elstrodt folgt. Die Definition und Berechnung von Volumen und Integral im ℝⁿ werden dabei ebenfalls ausführlich behandelt. Insbesondere werden Oberflächenintegrale eingeführt und der Integralsatz von Gauß bewiesen. Wenn die Zeit reicht, soll auch die Fouriertransformation diskutiert werden.

Der Stoff der Vorlesung ist für eine Vertiefung in den Gebieten Analysis, Angewandte Mathematik, Stochastik und Geometrie relevant. Auch für Studierende der Physik kann der Inhalt von Interesse sein.

Literatur:

1.)

J. Elstrodt : Maß- und Integrationstheorie, 2. Auflage, Springer 1999

2.)

H. Amann & J. Escher : Analysis III, Birkhäuser 2001

3.)

E. Kuwert : Analysis III, Skript

Inhalt:
In der linearen Algebra ging es um das Lösen von linearen Gleichungssystemen. Gegenstand der Vorlesung “Algebra und Zahlentheorie” ist das Lösen von Polynomgleichungen in einer Variablen. Aus der Schule bekannt ist der Fall quadratischer Gleichungen und ihrer Lösungsformel. Eines unserer Hauptresultate wird es sein, dass sich diese Lösungsformel nicht verallgemeinern lässt. Verwandt ist die Frage nach der Konstruierbarkeit mit Zirkel und Lineal.

Unser wesentiches Hilfsmittel ist die Theorie der algebraischen Körpererweiterungen mit dem Hauptsatz der Galoistheorie als Höhepunkt. Auf dem Weg werden wir auch andere algebraische Strukturen wie Gruppen und Ringe studieren.

Von besonderem Interesse ist der Fall von Gleichungen über den rationalen oder gar ganzen Zahlen. Dies ist Gegenstand der Zahlentheorie.

Literatur:

1.)

S. Bosch, Algebra

2.)

S. Lang, Algebra

3.)

F. Lorenz, Algebra 1

4.)

E. Artin, Galois theory

5.)

van der Waerden, Algebra 1

Inhalt:
Die Wahrscheinlichkeitstheorie setzt die Vorlesung Stochastik aus dem vergangenen Winter- und Sommersemester fort, in der Wahrscheinlichkeiten und zufällige Ereignisse mit weitgehend elementaren Methoden untersucht wurden. Aufgabe der Wahrscheinlichkeitstheorie ist es nun, zufallsabhängige Vorgänge systematisch auf maßtheoretischer Grundlage mathematisch zu beschreiben. Hierzu sind Vorkenntnisse aus der Analysis III nützlich und wünschenswert, aber nicht zwingend notwendig (die benötigten Grundlagen werden am Anfang der Vorlesung, allerdings kurz, wiederholt).

Ziel der Vorlesung ist die Herleitung einiger klassischer Grenzwertsätze (z.B. des starken Gesetzes großer Zahlen sowie des allgemeinen zentralen Grenzwertsatzes) sowie die Einführung allgemeiner bedingter Wahrscheinlichkeiten und Erwartungswerte.

Die Vorlesung ist Grundlage für alle weiterführenden Veranstaltungen aus dem Bereich der Stochastik und obligatorisch für alle, die eine Abschlussarbeit innerhalb der Stochastik schreiben oder dort einen Prüfungsschwerpunkt wählen möchten.

Literatur:

1.)

Bauer, H. : Wahrscheinlichkeitstheorie, 5. Aufl., de Gruyter, 2002

2.)

Kallenberg, O. : Foundations of Modern Probability, Springer, 2002

3.)

Klenke, A. : Wahrscheinlichkeitstheorie, 3. Aufl., Springer Spektrum, 2013

4.)

Rüschendorf, L. : Wahrscheinlichkeitstheorie, Springer Spektrum, 2016

5.)

Shiryaev, A. : Probability-1, 3. Aufl., Springer, 2016

Inhalt:
Die Differentialgeometrie, speziell die Riemannsche Geometrie, beschäftigt sich mit den geometrischen Eigenschaften gekrümmter Räume. Solche Räume treten auch in anderen Bereichen der Mathematik und Physik auf, beispielsweise in der geometrischen Analysis, der theoretischen Mechanik und der allgemeinen Relativitätstheorie.

Im ersten Teil der Vorlesung lernen wir Grundbegriffe der Differentialgeometrie (z. B. differenzierbare Mannigfaltigkeiten, Vektorbündel, Zusammenhänge und ihre Krümmung) und der Riemannschen Geometrie (Riemannscher Krümmungstensor, Geodätische, Jacobi-Felder etc.) kennen.

Im zweiten Teil betrachten wir das Zusammenspiel zwischen lokalen Eigenschaften Riemannscher Mannigfaltigkeiten wie der Krümmung und globalen topologischen und geometrischen Eigenschaften wie Kompaktheit, Fundamentalgruppe, Durchmesser, Volumenwachstum und Gestalt geodätischer Dreiecke.

Im Sommersemester 2018 ist eine Vorlesung Differentialtopologie geplant, im Wintersemester 2018/19 folgt Differentialgeometrie II mit Schwerpunkt spezielle Holonomie. Beide Vorlesungen können unabhängig voneinander als Fortsetzungen gewählt werden.

Literatur:

1.)

J. Cheeger, D. G. Ebin, Comparison Theorems in Riemannian Geometry, North-Holland, Amsterdam 1975.

2.)

S. Gallot, D. Hulin, J. Lafontaine, Riemannian Geometry, Springer, Berlin-Heidelberg-New York 1987.

3.)

D. Gromoll, W. Klingenberg, W. Meyer, Riemannsche Geometrie im Großen, Springer, Berlin-Heidelberg-New York 1975.

Inhalt:
In dieser Vorlesung sollen zunächst Begriffe und Methoden rund um Faserbündel behandelt werden. Diese bilden die grundlegenden Begriffe zur Behandlung vieler geometrischer Probleme auf gekrümmten Räumen sowie zur mathematischen Modellierung der vier Wechselwirkungen in der theoretischen Physik mittels Eichtheorien. So ist z.B. der Elektromagnetismus ein einfaches Beispiel einer Eichfeldtheorie. Als weiteres Beispiel werden wir als nichtabelsche Eichtheorie die Yang-Mills Theorie behandeln.

Im zweiten Teil der Vorlesung behandeln wir elliptische Differentialoperatoren auf Mannigfaltigkeiten und Bündeln, insbesondere den Laplaceoperator und soweit die Zeit zulässt den Diracoperator.

Literatur:

1.)

H. Baum, Eichfeldtheorie, Springer, 2014

Inhalt:
Partielle Differentialgleichungen sind Gleichungen, die einen Zusammenhang zwischen einer Funktion u, deren partiellen Ableitungen und weiteren gegebenen Funktionen beinhalten, z. B.

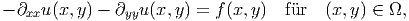
Literatur:

1.)

H.W. Alt, Lineare Funktionalanalysis, Springer (2006).

2.)

S. Bartels, Numerical approximation of partial differential equations, Springer (2016).

3.)

S. Brenner, R. Scott, Finite elements, Springer (2008).

4.)

D. Braess, Finite Elemente, Springer, Berlin (2007).

5.)

G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010).

6.)

L.C. Evans, Partial differential equations, AMS (2010).

Inhalt:
Modulformen sind komplex-analytische Funktionen auf der oberen komplexen Halbebene, welche eine bestimmte Funktionalgleichung und eine Wachstumsbedingung im Unendlichen erfüllen. Letztere garantiert, daß Modulformen eine komplexe Fourierreihen-Entwicklung besitzen. Die Theorie der Modulformen gehört also in den Bereich der Funktionentheorie, aber ihre zentrale Bedeutung liegt in ihrem Zusammenhang zur Zahlentheorie, zur Geometrie, und zur Darstellungstheorie. Daher resultieren auch die meisten ihrer Anwendungen.

Oft können Zählprobleme dadurch gelöst werden, indem man eine erzeugende Funktion aufstellt und deren Eigenschaften untersucht. In günstigen Situationen ist diese Funktion eine Modulform. Ihre Fourier-Koeffizienten sind dann die Lösung des Zählproblems. Daher rührt auch die Hauptanwendung von Modulformen in der Physik. Die Anzahl der Zustände eines quantenmechanischen Systems mit vorgegebenen Quantenzahlen wird durch die sogenannte Zustandssumme beschrieben, welche in günstigen Fällen eine Modulform ist.

Ein berühmtes Zählproblem in der Mathematik sind die Dimensionen der Darstellungen der grössten endlichen einfachen Gruppe, dem sogenannten Monster (mit ~ 10⁵³ Elementen). Die – inzwischen bewiesene – Monstrous Moonshine Vermutung besagt, dass die erzeugende Funktion dieser Dimensionen eine ganz bekannte Modulform ist (vgl. den Vorlesungskommentar zu „Monstrous Moonshine“).

Eine der faszinierendsten Anwendungen der Theorie der Modulformen ist der Beweis von Fermats letztem Satz, der besagt, daß aⁿ + bⁿ = cⁿ für n > 2 keine ganzzahlige Lösung außer a = b = 0 besitzt. Zugrunde liegt die Tatsache, daß die komplexe Kurve y² = x(x - aⁿ)(x - bⁿ) sehr viele Symmetrien besitzt und durch Modulformen eindeutig beschrieben werden kann. Solche Kurven heißen elliptische Kurven und sind das zentrale geometrische Objekt in der Theorie der Modulformen.

Das Ziel der Vorlesung ist es, eine elementare Einführung in die Konzepte der Modulformen und elliptischen Kurven zu geben mit Schwergewicht auf expliziten Rechnungen, während abstrakte Konzepte der Zahlentheorie weniger berücksichtigt werden.

Literatur:

1.)

Neil Koblitz, Introduction to Elliptic Curves and Modular Forms, Springer, 2nd edition, 1993

2.)

Don Zagier, Elliptic Modular Forms and Their Applications, in The 1-2-3 of Modular Forms, Springer, 2008

3.)

Fred Diamond, Jerry Shurman, A First Course in Modular Forms, Springer, 2005

4.)

Martin Eichler, Don Zagier, The Theory of Jacobi Forms, Birkhäuser, 1985

Inhalt:
Die Vorlesung baut auf der Vorlesung über Algebraische Topologie des Sommersemesters auf. Die Garbenkohomologie ist ein sehr flexibler Formalismus, der die singuläre Homologie stark erweitert und ihre Äquivalenz zu anderen Theorien wie der de-Rham-Kohomologie oder der Cech-Kohomologie zeigt. Die singuläre Kohomologie wird in dieser Vorlesung in den Hintergrund treten, aber die daraus gewonnene Anschauung ist grundlegend und dasselbe gilt für die dort besprochenen Grundaussagen der homologischen Algebra und Kategorientheorie, wie die lange exakte Homologiesequenz, adjungierte Funktoren, Limites und Kolimites und dergleichen mehr.

Literatur:

1.)

Godement, Cohomologie des faisceaux

2.)

Bredon, Sheaf cohomology

3.)

Soergel, Skript zur Garbenkohomologie

Inhalt:
Große Kardinalzahlen sind Zusatzannahmen, die über das übliche Axiomensystem ZFC hinausgehen und von denen noch kein Widerspruch hergeleitet wurde. Zum Beispiel benutzt der heute bekannte Beweis der Fermat’schen Vermutung einen Turm von unendlich vielen Grothendieck-Universen. Letzteres ist äquivalent zu unendlich vielen stark unerreichbaren Kardinalzahlen.

In dieser Vorlesung werden wir unter anderem unerreichbare, schwach kompakte, messbare und superkompakte Kardinalzahlen studieren und die Konsistenzstärkenhierarchie kennenlernen.

Literatur:

1.)

Akihiro Kanamori, The higher infinite. Large cardinals in set theory from their beginnings. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003

2.)

Thomas Jech, Set theory. The third millennium edition, revised and expanded. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003

3.)

Ralf Schindler, Set theory. Exploring independence and truth. Universitext. Springer, Cham, 2014

Inhalt:
In nichtparametrischen und hochdimensionalen statistischen Modellen ist die klassische Optimalitätstheorie der Maximum-Likelihood-Inferenz nicht anwendbar. Neue Grundlagen und Ideen wurden über die letzten Jahrzente entwickelt. In dieser Vorlesung wird die statistische Theorie in unenendlichdimensionalen Parameterräumen behandelt. Die mathematischen Grundlagen beinhalten Auszüge aus der Theorie der Gauß-Prozesse und der empirischen Prozese, Approximationstheorie sowie grundlegende Theorie von Funktionenräumen. Die Theorie der statistischen Inferenz in solchen Modellen – Hypothesentests, Schätzer und Konfidenzbereiche – wird im sogenannten Minimax-Paradigma der Erntscheidungstheorie entwickelt. Dies beinhaltet Projektionsschätzern und nichtparametrischer Maximum-Likelihood-Schätzung. Zuletzt wird die Theorie adaptiver Inferenz in nichtparametrischen Modellen entwickelt.________________________

Inhalt:
In dieser Vorlesung werden die Grundlagen der geometrischen Modelltheorie behandelt. Grundbegriffe wie Quantorenelimination oder Kategorizität werden eingeführt. Eine Theorie habe Quantorenelimination, falls jede Formel äquivalent zu einer quantorenfreien Formel ist. Für die Theorie algebraisch abgeschlossener Körper einer festen Charakteristik ist dies dazu äquivalent, dass die Projektion einer Zariski-konstruktiblen Menge wiederum Zariski-konstruktibel ist.

Eine Theorie heiße ℵ₁-kategorisch, wenn alle Modelle der Mächtigkeit ℵ₁ isomorph sind. Ein typisches Beispiel ist die Theorie unendlich dimensionaler ℚ-Vektorräume. Das Ziel der Vorlesung ist es, die Sätze von Baldwin-Lachlan und von Morley zu verstehen, um ℵ₁-kategorische Theorien zu charakterisieren.

Literatur:

1.)

B. Poizat : Cours de théorie des modèles, (1985), Nur al-Mantiq wal-Ma’rifah.

2.)

K. Tent, M. Ziegler : A Course in Model Theory, (2012), Cambridge University Press.

Inhalt:
Die Moonshine-Vermutung stellt einen unerwarteten Zusammenhang her zwischen der sogenannten Monster-Gruppe, das ist die größte sporadische Gruppe, sowie einer wichtigen, auf der oberen Halbebene holomorphen Funktion, nämlich der Modulfunktion j.

In der Klassifikation der endlichen einfachen Gruppen treten 26 Ausnahmegruppen in Erscheinung, die „sporadische“ Gruppen. Die Monster-Gruppe M ist die größte unter diesen. Sie besitzt

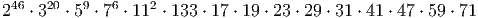
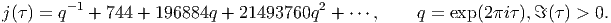
Ziel der Vorlesung ist es, Aussage sowie Grundzüge des Beweises der „Monstrous-Moonshine“-Vermutung zu erarbeiten. Dazu werden die wesentlichen Grundbegriffe und Ergebnisse aus der Theorie der endlichen Gruppen, der Lie-Algebren, deren Darstellungen, der Modulformen sowie aus der konformen Feldtheorie eingeführt. Dazu werden auch die grundlegenden Konstruktionen von Vertexoperator-Algebren diskutiert. Vorkenntnisse aus der Physik werden nicht vorausgesetzt.

Literatur:

1.)

T. Gannon, Moonshine Beyond the Monster, Cambridge University Press, 2006

2.)

R. Borcherds, Proceedings of the I.C.M., Vol. I (Berlin, 1998). Doc. Math. 1998, Extra Vol. I, 607–615, http ://math.berkeley.edu/ reb/papers/icm98/icm98.pdf

Inhalt:
The course’s aim is to give an introduction into numerical methods for the solution of optimization problems in science and engineering. The focus is on continuous nonlinear optimization in finite dimensions, covering both convex and nonconvex problems. The course is accompanied by intensive computer exercises and divided into four major parts :

1.

Fundamental Concepts of Optimization : Definitions, Types, Convexity, Duality

2.

Unconstrained Optimization and Newton Type Algorithms : Stability of Solutions, Gradient and Conjugate Gradient, Exact Newton, Quasi-Newton, BFGS and Limited Memory BFGS, and Gauss-Newton, Line Search and Trust Region Methods, Algorithmic Differentiation

3.

Equality Constrained Optimization Algorithms : Newton Lagrange and Generalized Gauss-Newton, Range and Null Space Methods, Quasi-Newton and Adjoint Based Inexact Newton Methods

4.

Inequality Constrained Optimization Algorithms : Karush-Kuhn-Tucker Conditions, Linear and Quadratic Programming, Active Set Methods, Interior Point Methods, Sequential Quadratic and Convex Programming, Quadratic and Nonlinear Parametric Optimization

Bitte informieren Sie sich auf der Webseite des Lehrstuhls oder in HISinOne über weitere Angaben._________________________________________________________________________________________________________

Inhalt:
Ziel der Vorlesung ist die Lösung von elliptischen und parabolischen Randwertaufgaben. Es sollen einerseits klassische Lösungstechniken behandelt werden, andererseits Lösungen in L²-Sobolevräumen. Erste Anwendungen in der Geometrie werden diskutiert. Für den zweiten Teil wird aus der Funktionalanalysis das Kapitel zur Hilbertraumtheorie benötigt, dieses kann auch ad hoc studiert werden.

Die Vorlesung wendet sich an Studierende im Master sowie im Bachelor, besonders wenn eine Bachelorarbeit im Bereich Geometrische Analysis angestrebt wird.

Literatur:

1.)

L. C. Evans : Partial Differential Equations, Graduate Studies in Math., AMS 2010.

2.)

D. Gilbarg, N. Trudinger : Elliptic Partial Differential Equations of Second Order, Classics in Mathematics, Springer 2001.

3.)

A. Friedman : Partial Differential Equations of Parabolic Type, Dover Books in Mathematics 2008.

Inhalt:
Die Vorlesung ist die erste Veranstaltung im Studiengang Master of Science Mathematik, Studienschwerpunkt Wahrscheinlichkeitstheorie, Finanzmathematik und Statistik, insbesondere in der Profillinie Finanzmathematik. Sie schließt direkt an die Vorlesung Wahrscheinlichkeitstheorie aus dem WS 2016/17 an.

Gegenstand der Vorlesung ist eine Einführung in die Theorie der stochastischen Prozesse ; es werden unter anderem folgende Themen behandelt :

• Stochastische Basen, Stoppzeiten
• Martingale, Semimartingale
• Wiener-Prozesse, Poisson-Prozesse
• Quadratische Variation, previsibler Kompensator
• Itô-Formel, stochastisches Exponential

Im Sommersemester 2018 wird diese Veranstaltung durch die Vorlesung Stochastische Integration und Finanzmathematik fortgeführt.

Literatur:

1.)

S.N. Cohen, R.J. Elliott : Stochastic Calculus and Applications. Birkhäuser, 2015

2.)

J. Jacod, A. Shiryaev : Limit Theorems for Stochastic Processes. Springer, 2003

3.)

A. Klenke : Wahrscheinlichkeitstheorie. Springer, 2008

Inhalt:
Die numerischen Methoden zur Behandlung elliptischer partieller Differentialgleichungen führen zu Schwierigkeiten, wenn das Problem kleine Parameter enthält oder Nebenbedingungen erfüllt werden müssen. Diese Aspekte treten beispielsweise bei der mathematischen Beschreibung von Festkörpern und Fluiden auf. In der Vorlesung sollen die theoretischen Eigenschaften solcher Modelle analysiert und geeignete numerische Verfahren entwickelt werden.

Literatur:

1.)

S. Bartels : Numerical Approximation of Partial Differential Equations. Springer, 2016.

2.)

D. Braess : Finite Elemente. Springer, 2007.

3.)

D. Boffi, F. Brezzi, M. Fortin : Mixed Finite Element Methods and Applications. Springer, 2013.

4.)

M. Dobrowolski : Angewandte Funktionalanalysis. Springer, 2005.

5.)

P. Knabner, L. Angermann : Numerical Methods for Elliptic and Parabolic PDEs. Springer, 2000.

6.)

C. Grossmann, H.-G. Roos : Numerische Behandlung partieller Differentialgleichungen. Springer, 2005.

Inhalt:
The aim of this course is the application of the R programming environment to various topics of financial mathematics, among others are the calculation and visualization of interest rates, option prices, loss distributions and risk measures. Participants are expected to have some basic knowledge in using R as students of B.Sc. Mathematics usually acquire in the practical exercises of stochastics.

With help of these tools, we develop some programs for bootstrapping zero rates, pricing vanilla options in binomial trees and exotic options in time-continuous models via Monte Carlo methods. We also regard some aspects of hedging and convergence in this context. Further we discuss the implementation of risk measures, the sampling of loss distributions in elementary credit risk models. Depending on the time left, we may additionally discuss the simulation of (approximate) solutions to stochastic differential equations.

The course, which is taught in English, is offered for the second year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. (possibly also B.Sc.) Mathematics.

Literatur:

1.)

Hull, J.C. : Options, Futures, and other Derivatives, 7th ed., Prentice Hall, 2009

2.)

Lai, T.L., Xing, H. : Statistical Models and Methods for Financial Markets, Springer, 2008

3.)

Seydel, R.U. : Tools for Computational Finance, 4th ed., Springer, 2009

4.)

Any introductory book to the R programming environment, e.g.,
Brown, J., Murdoch, D.J. : A First Course in Statistical Programming with R, Cambridge University Press, 2007

Inhalt:

Diese Vorlesung findet nicht statt.________________________________________________________________________

Inhalt:
This course covers an introduction to financial markets and products. Besides futures and standard put and call options of European and American type we also discuss interest-rate sensitive instruments such as swaps.

For the valuation of financial derivatives we first introduce financial models in discrete time as the Cox-Ross-Rubinstein model and explain basic principles of risk-neutral valuation. Finally, we will discuss the famous Black-Scholes model which represents a continuous time model for option pricing.

In addition to the lecture there will be general tutorial as well as a practical tutorial where the theoretical methods taught in the lecture will be practically implemented (mostly in the software R) and applied to real data problems.

The course, which is taught in English, is offered for the first year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. and B.Sc. Mathematics and M.Sc. Volkswirtschaftslehre.

For students who are currently in the B.Sc. Mathematics program, but plan to continue with the special profile Finanzmathematik within the M.Sc. Mathematics, it is recommended to credit this course for the latter profile and not for B.Sc. Mathematics.

Literatur:

1.)

Chance, D.M., Brooks, R. : An Introduction to Derivatives and Risk Management, (8th ed.), South-Western, 2009

2.)

Hull, J.C. : Options, Futures, and other Derivatives (7th ed.), Prentice Hall, 2009

3.)

Shreve, S.E. : Stochastic Calculus for Finance I : The Binomial Asset Pricing Model, Springer Finance, 2005

4.)

Strong, R.A. : Derivatives. An Introduction, (2nd ed.), South-Western, 2004

Inhalt:
This course provides an introduction to fixed income markets. We focus on bootstrapping of yield curves and the pricing of interest-rate sensitive instruments. For this purpose we will meet the most widely used model approaches such as short-rate, HJM and market models.

The financial crisis causes many changes in the valuation of interest-rate products. For this reason we address the multiple-curve approach that deals with this new market situation.

In addition to the lecture there will be general tutorial where the theoretical methods taught in the lecture will be deepened by exercises as well as practically implemented (mostly in the software R) and applied to real data problems.

The course, which is taught in English, is offered for the first year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. and B.Sc. Mathematics and M.Sc. Volkswirtschaftslehre.

Literatur:

1.)

Hull, J.C. : Options, Futures, and other Derivatives (7th ed.), Prentice Hall, 2009

2.)

Shreve, S.E. : Stochastic Calculus for Finance I : The Binomial Asset Pricing Model, Springer Finance, 2005

3.)

Filipovic, D. : Term-Structure Models, Springer Finance, 2009

Inhalt:
Die Theorie rauher Pfade ermöglicht einen pfadweisen Zugang zur Analyse stochastischer Differentialgleichungen ; dies gestattet Vereinfachungen und Verallgemeinerungen von Resultaten aus der stochastischen Analysis.

Das Ziel der Vorlesung ist eine Einführung in die Theorie der rauhen Pfade ; es werden unter anderem folgende Themen behandelt :

• Räume rauher Pfade
• Die Brown’sche Bewegung als rauher Pfad
• Integration bezüglich rauher Pfade
• Stochastische Integration und die Itô-Formel
• Rauhe Differentialgleichungen und stochastische Differentialgleichungen
• Gauß’sche rauhe Pfade

Literatur:

1.)

P.K. Friz, M. Hairer : A Course on Rough Paths. Springer, 2014

Inhalt:
In den Lebenswissenschaften werden an vielen Stellen stochastische Prozesse einesetzt, um natürliche Phänomene zu beschreiben. Wir befassen uns mit folgenden Bereichen :

• Populationsgenetik : Dieser Teilbereich der Evolutionstheorie beschreibt die zeitliche Entwicklung von Allelhäufigkeiten in einer Population.
• Biochemische Reaktionen : Durch die geringe Zahl an Reaktionspartnern kommt es in Zellen zu zufälligen Konzentrationsschwankungen einzelner Molekülsorten.
• Neurobiologie : Das Feuern von Neuronen unterliegt der Netzwerkstruktur im Gehirn, mit sowohl anregenden als auch hemmenden Verbindungen zwischen einzelnen Neuronen.
• Epidemiologie : Die Ausbreitung von Krankheiten kann durch Populationsmodelle beschrieben werden, bei denen Individuen gesund, erkrankt oder immun gegen eine Krankheit sind.

Die mathematische Modellierung in alle n Bereichen erfolgt mittels Markov-Prozessen. In der Vorlesung werden wir sowohl Wert auf die konkrete biologische Anwendung legen, als auch auf die nötigen mathematischen Konzepte.

Literatur:

1.)

D. Anderson, T. Kurtz. Stochastic Analysis of Biochemical Systems. Springer, 2015.

2.)

L. Allen. An Introduction to Stochastic Processes with Applications to Biology. Taylor & Francis, 2010.

3.)

W. Ewens. Mathematical Population Genetics 1. Theoretical Introduction. Springer, 2004.

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich (im Zwei-Hauptfächer-Bachelor : „Optionsbereich“) angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Leistungsnachweis :

• Teilnahme an der Einführungsveranstaltung (voraussichtlich in der ersten Vorlesungswoche ; Termin wird kurzfristig im Vorlesungsverzeichnis bekanntgegeben)
• regelmäßige Teilnahme an der Tutorenbesprechung
• zwei gegenseitige Tutoratsbesuche mit einem anderen Modulteilnehmer, welcher nach Möglichkeit die gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der Einführungsveranstaltung)
• Schreiben eines Erfahrungsberichts, der an den betreuenden Dozenten geht

In Ermangelung eines passenden Wahlbereichs kann das Modul im Lehramtsstudiengang in dieser Form leider nicht angeboten werden._____________________________________________________________

2b. Fachdidaktik

Einführung in die Fachdidaktik der Mathematik

Mathematik-Studierende im polyvalenten Zwei-Hauptfächer-Bachelor-Studiengang, die die Lehramtsoption wählen, müssen im Optionsbereich u.a. das Fachdidaktikmodul Einführung in die Fachdidaktik der Mathematik (5 ECTS-Punkte) absolvieren.

Studierende im Zwei-Hauptfächer-Bachelor-Studiengang, die nicht die Lehramtsoption wählen oder sich im Nachhinein dagegen entscheiden, können das Modul als Berufsfeldorientierte Kompetenzen (BOK) anrechnen lassen.

Dieses Modul wird im Wintersemester 2017/18 erstmalig angeboten, und zwar auf zweierlei Weise :

• Als eigene Lehrveranstaltung Einführung in die Fachdidaktik der Mathematik (Vorlesung mit Übungen ; 4 SWS, 5 ECTS) ; siehe Seite 65.
• Als die eigentlich für das Lehramt nach GymPO angebotene Veranstaltung Didaktik der Algebra und Analysis (Vorlesung mit Übungen ; 2,5 SWS, 3 ECTS), die durch ein zusätzliches „eingebettetes Seminar“ auf 5 ECTS-Punkte aufgewertet wird ; siehe Seite 64.

Sie haben die freie Wahl zwischen beiden Varianten ; bitte belegen Sie die von Ihnen gewählte Vorlesung über HISinOne bis 30.09.2017.

Es ist geplant, dass das Modul Einführung in die Fachdidaktik der Mathematik in jedem Semester angeboten wird.

Inhalt:

Die Vorlesung bietet eine Einführung in eine konstruktivistisch-systemische Didaktik, welche auf Lernumgebungen basiert. Ein hoher Wert wird auf die Praxis gelegt. Die Vorlesung selbst ist handlungs- und erlebnisorientiert. So erleben die Teilnehmer konkrete Lernumgebungen, die sie z. B. im Praxissemester oder im eingebetteten Seminar (2-HF-Bachelor) durchführen können.

2-HF-Bachelor-Studierende besuchen zusätzlich das (in die Veranstaltung eingebettete) Seminar, in dem ein Unterrichtsversuch durchgeführt und beobachtet wird. Der Schulversuch wird in drei kompakten Terminen vorbereitet und reflektiert.

Kommentar :
Das eingebettetes Seminar besteht aus 3 zweistündige Termine (Di 17–19 Uhr) zur Planung, Durchführung und Reflexion eines Unterrichtsversuches mit Ausarbeitung.
Die Vorlesung kann von Studierenden nach GymPO und 2-HF-Bachelor belegt werden.
Das eingebettete Seminar ist nur für 2-HF-Bachelor-Studierende verpflichtend.

Bitte beachten Sie den Kommentar auf Seite 63._____________________________________________________

Inhalt:

Diese Einführungsveranstaltung in die Fachdidaktik der Mathematik wird in Kooperation der Universität Freiburg, der Pädagogischen Hochschule Freiburg (zusammengeschlossen im Freiburg Advanced Center of Education – FACE), sowie Vertretern des gymnasialen Studienseminars konzipiert, sodass die Inhalte auf die späteren Anforderungen im Master und im Referendariat abgestimmt sind.

Bei den Inhalten handelt es sich um mathematikdidaktische Ideen und Prinzipien, die für den Mathematikunterricht in der Sekundarstufe I und II eine zentrale Rolle spielen (z.B. Verstehensorientierung, Entdeckendes Lernen, Prinzipien des Übens u.v.m.). Die Inhalte werden an unterschiedlichen Fachinhalten der Schulmathematik der Jgst. 5 bis 12 erarbeitet. Dabei werden Bezüge zwischen Schulmathematik und den fachwissenschaftlichen Vorlesungen der Studierenden hergestellt.

Zielgruppe der Veranstaltung sind in erster Linie Studierende des 2-HF-Bachelors. Die Veranstaltung wird mit einer Klausur abgeschlossen.

Bitte beachten Sie den Kommentar auf Seite 63._____________________________________________________

Inhalt:

MINT steht für die Vernetzung von Mathematik, Informatik, Naturwissenschaft und Technik. Der erste Buchstabe steht für Mathematik, jedoch vereint Robotik alle ( !) vier Buchstaben gleichzeitig und eignet sich exemplarisch für die Schule, sowohl im Rahmen einer AG, von Projekttagen oder im Unterricht.

Das Seminar besteht aus zwei Teilen. Zuerst wird aus Fischertechnik ein mobiler Roboter gebaut und mit immer feineren Methoden mit der kindgerechten Software RoboPro programmiert. Im Vordergrund steht ein konstruktivistisches und kommunikatives Lernverständnis. Wie können geeignete Lernumgebungen für Jugendliche so geschaffen werden, dass Lernerfolg, Nachhaltigkeit und Spielfreude gewährleistet ist ?

Der zweite Teil besteht in der Durchführung eines zweitägigen Workshops (Freitagnachmittag bis Sonntagmorgen), der im Seminar geplant und von je zwei Teilnehmern in den Semesterferien durchgeführt wird.

Es sind keinerlei Vorkenntnisse erforderlich.____________________________________________________________

Inhalt:
Der Einsatz von Unterrichtsmedien im Mathematikunterricht gewinnt sowohl auf der Ebene der Unterrichtsplanung wie auch der der Unterrichtsrealisierung an Bedeutung. Vor dem Hintergrund konstruktivistischer Lerntheorien zeigt sich, dass der reflektierte Einsatz unter anderem von Computerprogrammen die mathematische Begriffsbildung nachhaltig unterstützen kann. So erlaubt beispielsweise das Experimentieren mit Computerprogrammen mathematische Strukturen zu entdecken, ohne dass dies von einzelnen Routineoperationen (wie z. B. Termumformung) überdeckt würde. Es ergeben sich daraus tiefgreifende Konsequenzen für den Mathematikunterricht. Von daher setzt sich dieses Seminar zum Ziel, den Studierenden die notwendigen Entscheidungs- und Handlungskompetenzen zu vermitteln, um zukünftige Mathematiklehrer auf ihre berufliche Tätigkeit vorzubereiten. Ausgehend von ersten Überlegungen zur Unterrichtsplanung werden anschließend Computer und Tablets hinsichtlich ihres jeweiligen didaktischen Potentials untersucht.

Die dabei exemplarisch vorgestellten Systeme sind :

• dynamische Geometrie-Software : Geogebra
• Tabellenkalkulation : Excel
• Apps für Smartphones und Tablet mit dem Schwerpunkt One Note

Jeder Studierende soll Unterrichtssequenz ausarbeiten, die dann in den Übungen besprochen werden.___________________________________________________________________________________________________________

Inhalt:
In der praktischen Übung zur Numerikvorlesung werden die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet. Dies wird in der Programmiersprache C++ sowie mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

S. Bartels : Numerik 3x9. Springer, 2016.

2.)

R. Plato : Numerische Mathematik kompakt. Vieweg, 2006.

3.)

R. Schaback, H. Wendland : Numerische Mathematik. Springer, 2004.

4.)

J. Stoer, R. Burlisch : Numerische Mathematik I, II. Springer, 2007, 2005.

5.)

G. Hämmerlin, K.-H. Hoffmann : Numerische Mathematik. Springer, 1990.

6.)

P. Deuflhard, A. Hohmann, F. Bornemann : Numerische Mathematik I, II. DeGruyter, 2003.

Inhalt:
In der praktischen Übung werden die numerischen Verfahren aus der Vorlesung ”Einführung in die Theorie und Numerik partieller Differentialgleichungen” besprochen und implementiert. Ziel ist die Entwicklung eines effizienten Programmes zur Lösung elliptischer Randwertprobleme mit Hilfe von Finite-Elemente-Verfahren. Als Programmiersprache soll dabei C/C++ verwendet werden, so dass Programmiererfahrung erwartet wird, in dem Umfang, wie sie etwa in einem Praktikum zur Numerik I/II erworben werden kann. Studierenden, die vorhaben, in der Angewandten Mathematik eine Zulassungs-, Bachelor- oder Masterarbeit zu schreiben, wird die Teilnahme am Praktikum dringend empfohlen.

Literatur:

1.)

H.W. Alt, Lineare Funktionalanalysis, Springer (2006).

2.)

S. Bartels, Numerical approximation of partial differential equations, Springer (2016).

3.)

S. Brenner, R. Scott, Finite elements, Springer (2008).

4.)

D. Braess, Finite Elemente, Springer, Berlin (2007).

5.)

G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010).

6.)

L.C. Evans, Partial differential equations, AMS (2010)

Inhalt:
In der praktischen Übung sollen die in der Vorlesung entwickelten und analysierten Verfahren praktisch umgesetzt und experimentell getestet werden. Dies wird mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse und Erfahrung im Umgang mit MATLAB werden vorausgesetzt.

Literatur:

1.)

S. Bartels : Numerical Approximation of Partial Differential Equations. Springer, 2016.

2.)

D. Braess : Finite Elemente. Springer, 2007.

3.)

D. Boffi, F. Brezzi, M. Fortin : Mixed Finite Element Methods and Applications. Springer, 2013.

4.)

M. Dobrowolski : Angewandte Funktionalanalysis. Springer, 2005.

5.)

P. Knabner, L. Angermann : Numerical Methods for Elliptic and Parabolic PDEs. Springer, 2000.

6.)

C. Grossmann, H.-G. Roos : Numerische Behandlung partieller Differentialgleichungen. Springer, 2005.

Inhalt:
 
Variationsrechnung ist eines der ältesten Teilgebiete der Analysis. In der Variationsrechnung geht es darum, Extremstellen von Funktionalen zu finden. Viele Fragestelle aus der Geometrie (Geodätischen, d.h. kürzeste Verbindung zwischen zwei Punkten ; Minimalflächen), der partiellen Differentialgleichungen, und der Physik (klassischen Mechanik, Optik und Feldtheorie) führen auf unendlichendimensionale Extremwertaufagben.

Wir erarbeiten unter anderem, je nach Interesse, folgende Themen :

∙ notwendige Bedingungen für Minimierer, Euler-Lagrange-Differentialgleichungen

∙ Minimalflächen vom Rotationstyp

∙ geodätische Kurven

∙ den Satz von Emmy Noether über Erhaltungsgrößen in physikalischen Systemen.

Literatur:

1.)

Kielhöfer, Hansjörg ; Variationsrechnung (Vieweg+Teubner, 2010)

Inhalt:
Dynamische Systeme treten in vielen Kontexten auf, nämlich überall da, wo sich etwas im Laufe der Zeit verändert. Mathematisch beschreiben kann man solche Vorgänge als Fluss von Vektorfeldern oder in diskreter Zeit als Iteration von Abbildungen.

In diesem Proseminar geht es um die qualitative Untersuchung solcher Systeme, also um das grobe Bild der Lösungen in Abhängigkeit von vorgegebenen Anfangsbedingungen. Von besonderem Interesse sind dabei Fixpunkte und periodische Lösungen und ihre Stabilität unter Störungen. Viele allgemeine Phänomene lassen sich gut an Beispielen untersuchen, so dass es in fast allen Vorträgen nicht nur Theorie gibt, sondern auch sehr konkrete dynamische Systeme, deren Eigenschaften untersucht werden.

Literatur:

1.)

A. Katok, B. Hasselblatt, Introduction to the modern theory of dynamical systems, Cambridge Univ. Press, 2006

Inhalt:
Dieses Proseminar verknüpft Analysis und Zahlentheorie. Die Analysis beruht ganz wesentlich auf dem Begriff der ε-Umgebung – Zahlen sind „nah“ wenn ihre Differenz einen kleinen Betrag hat. Man kann allerdings auch ganze Zahlen „nah“ nennen, wenn ihre Differenz durch eine hohe Potenz einer Primzahl p teilbar ist. Ähnlich wie die reellen Zahlen aus den rationalen entstehen, indem man fordert, dass alle Cauchyfolgen konvergieren sollen, kann man die rationalen Zahlen auch erweitern, indem man dasselbe für diesen völlig anderen Begriff von ε-Umgebung fordert. Und genau dies sind die berühmten p-adischen Zahlen. Es gibt Folgen, die nicht in den reellen Zahlen konvergieren, aber in den p-adischen – und sogar Folgen, die sowohl p-adisch wie auch reell konvergieren, aber mit unterschiedlichen Grenzwerten.

Ein Großteil der klassischen Analysis lässt sich auch für die p-adischen Zahlen entwickeln, und sehr vieles ist ganz ähnlich zur üblichen Analysis, und gleichzeitig doch auch ganz anders. Man muss sich selbst damit beschäftigen, um diese spannenden Phänomene wirklich verstehen zu können. Und genau dies wollen wir in diesem Proseminar tun.

Literatur:

1.)

Gouvêa : p-adic Numbers, Universitext, Springer-Verlag, Berlin, 1993

2.)

Katok : p-adic Analysis Compared with Real, AMS, 2007 Neukirch : Algebraische Zahlentheorie, Springer

3.)

Werner : Nicht-archimedische Zahlen, Vorlesung Frankfurt, 2012

4.)

Dieck : Topologie, de Gruyter Lehrbuch, Walter de Gruyter and Co., Berlin, 1991

5.)

Jänich : Topologie, Springer, 1980

Inhalt:
Classical physics does not predict the behaviour of atoms and molecules correctly. Indeed, classically, Coulomb’s law implies that the electron of the hydrogen atom should orbit around the proton, and thus the electron continuously radiates energy and causes the hydrogen atom to collapse. This contradicts the observed stability of the hydrogen atom. One of the major triumphs of quantum mechanics is its explanation for the stability of atoms.

Mathematically, a classical mechanical system can be described by a so–called symplectic manifold M called the state space, and the observables are functions on M. A quantum mechanical system, on the other hand, is described by a Hilbert space, and the observables are “operators” on this Hilbert space. A process which roughly associates to a classical theory a quantum theory is called “quantization”. Ideally, one would like to associate to each classical observable a quantum observable, but it is impossible to achieve this : there are no go theorems. In practice, one has to lower one’s expectation so that a reasonable quantization process can be constructed.

The goal of this seminar is to study one particular method of quantization called geometric quantization. Position space quantization, momentum space quantization and holomorphic quantization are particular instances of geometric quantization. In geometric quantization, one constructs the Hilbert space from the square integrable sections of a so–called complex line bundle over M.

Within the seminar, we will motivate and introduce the mathematical notions that are needed for geometric quantization, starting from Newtonian mechanics. Background knowledge from physics is helpful but is not required.

Literatur:

1.)

Brian C. Hall, Quantum theory for mathematicians, volume 267 of Graduate Texts in Mathematics, Springer, New York, 2013

2.)

Nicholas Woodhouse, Geometric quantization, The Clarendon Press, Oxford University Press, New York, 1980, Oxford Mathematical Monographs

Inhalt:
Mathematische Knoten sind stetige injektive Abbildungen S¹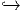S³ bzw. in höherdimensionaler Verallgemeinerung Sⁿ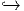Sⁿ⁺². Die Knotentheorie beschäftigt sich mit der Frage nach Invarianten, die direkt aus einem Knotendiagramm berechenbar sind und mit denen man verschiedene Knoten voneinander unterscheiden kann. Das Ziel des Seminars ist es, ein paar der topologischen und algebraischen Invarianten von Knoten kennenzulernen. In diesem Zusammenhang geht es natürlich auch darum, einige Grundbegriffe der algebraischen Topologie (Fundamentalgruppen, Homologie) kennenzulernen bzw. zu vertiefen. Ein paar algebraische Ausflüge zu Zopfgruppen, Hecke-Algebren und polynomialen Knoten runden das Seminar ab.

Literatur:

1.)

A. Hatcher. Algebraic topology, Cambridge University Press, 2002.

2.)

A. Kawauchi. A survey of knot theory. Birkhäuser, 1996.

3.)

D. Rolfsen. Knots and links. Amer. Math. Soc., 1976

Inhalt:
 
Distributionen werden nicht nur vielfältig in der Mathematik selbst genutzt, z.B. als Fundamentallösungen von partiellen Differentialgleichungen und Greenfunktionen, sondern treten auch in der Physik in den verschiedensten Kontexten auf, z.B. als Masseverteilungen von Teilchen oder als Propagatoren in der Quantenfeldtheorie.

Das Verhalten der Singularitäten solcher Distributionen kodiert das Verhalten von Lösungen. Mikrolokale Analysis analysiert das systematisch. Viele der zugrundeliegenden Ideen kommen aus der Physik insbesondere aus der geometrischen Optik.

Der Großteil des Seminars wird mikrolokale Analysis auf dem ℝⁿ behandeln. Erst im hinteren Teil bei den Anwendungen werden auch Mannigfaltigkeiten vorkommen.

Das ausführliche Seminarprogramm finden Sie auf obiger Webseite.

Literatur:

1.)

A. Grigis, J. Sjöstrand : Microlocal Analysis for Differential Operators, Cambridge University Press, 1994

2.)

M.A. Shubin : Pseudodifferential Operators and Spectral Theory, Springer, 2001

Inhalt:
Seit den 1980er Jahren entwickelt Stevo Todorcevic eine Theorie von Metriken und Ultrametriken auf den Ordinalzahlen. Viele dieser Metriken werden durch absteigende (und daher nur endlich lange) Folgen auf den Ordinalzahlen, sogenannte Todorcevic Walks, definiert. Mit der metrischen Analyse lassen sich unter anderem Färbungstheoreme herleiten : Zum Beispiel gilt auf der kleinsten überabzählbaren Kardinalzahl im starken Sinn das Gegenteil des Ramseysatzes über Färbungen von Paarmengen natürlicher Zahlen mit endlich vielen Farben. Die Farben werden aus einem geeigneten absteigenden Gang definiert.

Literatur:

1.)

Stevo Todorcevic, Walks on ordinals and their characteristics. Progress in Mathematics, 263. Birkhäuser Verlag, Basel, 2007.

2.)

Justin Tatch Moore, A solution to the L-space problem. J. Amer. Math. Soc. 19 (2006), no. 3, 717–736.

Inhalt:
 
Ein Körper sei differentiell, falls es einen additiven Homomorphismus gibt, welcher das Leibniz’sche Gesetz erfüllt. Existentiell abgeschlossene Modelle in der Klasse differentieller Körper heißen differentiell abgeschlossene Körper. Ihre Theorie ist axiomatisierbar und ω-stabil unendlichen Ranges (in Charakteristik 0). G. Sacks beschrieb die Theorie differentiell abgeschlossener Körper als das least misleading Beispiel einer ω-stabilen Theorie.

Im Seminar lernen wir differentiell agbeschlossene Körper und ihre modelltheoretischen Eigenschaften kennen. Insbesondere werden wir zwei verschiedene Axiomatisierungen sehen, so wie die Beschreibung von Typen, Stabilität und Quantorenelimination in der Ringsprache zusammen mit einem Symbol für die Ableitung. Dazu ergänzend werden wir den Fall positiver Charakteristik studieren.

Literatur:

1.)

D. Marker : Introduction to the model theory of differential fields, preprint, MSRI.

2.)

D. Marker, M. Messmer, A. Pillay : Model Theory of Fields, (1996), Springer-Verlag.

3.)

K. Tent, M. Ziegler : A Course in Model Theory, (2012), Cambridge University Press.

Inhalt:
Unter mathematischer Modellierung versteht man die Beschreibung realer Vorgänge durch mathematische Objekte oder Formulierungen wie beispielsweise Minimierungsprobleme oder Differentialgleichungen. Im Seminar sollen verschiedene Prozesse wie der Abbau von Alkohol im Körper, das Schmelzen eines Eiswürfels im Wasserglas und die Funktionsweise eines Doppelklingenrasieres mathematisch beschrieben und auf Basis der Modelle vorhergesagt werden.

Die Seminarthemen sind auch für Lehramtsstudierende geeignet.

Literatur:

1.)

A. Eck, H. Garcke, P. Knabner : Mathematische Modellierung, Springer, 2011.

2.)

C.P. Ortlieb, C. v. Dresky, I. Gasser, S. Günzel : Mathematische Modellierung, Springer-Spektrum, 2009.

3.)

C. Kohlmeier : Einführung in die mathematische Modellierung, Vorlesungsskript Uni Oldenburg, 2006.

Inhalt:
Die numerische Lösung von partiellen Differentialgleichungen ist oft nur sehr aufwendig zu berechnen und daher ist man an Methoden interessiert, die die Komplexität der Berechnung reduzieren. Inzwischen gibt es mehrere Methoden um die Komplexität effektiv zu reduzieren. Die Methode der reduzierten Basen ist z.B. anwendbar auf Randwertprobleme, die von einem Parameter abhängen für den Fall, dass man immer wieder für viele Parameter Lösungen berechnen will. Die Methode besteht nun darin, im Voraus für eine endliche Anzahl von Parametern Lösungen sehr genau zu berechnen. Diese endlich vielen Lösungen betrachtet man als Basis eines neuen endlich dimensionalen Vektorraums und löst für neue Parameter das Problem auf diesem neu definierten endlich dimensionalen Vektorraum. Wie die Praxis zeigt, kann man mit relativ wenigen Basisfunktionen neue Lösungen mit hinreichender Genauigkeit effizient berechnen. Weitere Methoden sind die ”proper orthogonal decomposition”-Verfahren und die Homogenisierung. In diesem Seminar werden wir verschiedene Methoden besprechen und die mathematischen Grundlagen analysieren.

Literatur:

1.)

B. Haasdonk, Effiziente und gesicherte Modellreduktion für parametrisierte dynamische Systeme, Automatisierungstechnik, 58 (2010) 8.

2.)

B. Haasdonk und M. Ohlberger : Efficient reduced models and a posteriori error estimation for parametrized dynamical systems by offline/online decomposition, Mathematical and Computer Modelling of Dynamical Systems : Methods, Tools and Applications in Engineering and Related Sciences, 17 :2, 145–161, 2011.

3.)

B. Haasdonk : Vorlesungsskript Reduzierte-Basis-Methoden, Preprint IANS, Uni Stuttgart, 2011.

4.)

M. Ohlberger, Skript zur Vorlesung Numerische Mehrskalenmethoden und Modellreduktion, SoSe 2017, Uni Münster.

5.)

J. Brunken, Modellreduktion für parametrisierte dynamische Systeme, Seminarausarbeitung, Universität Münster.

Inhalt:
Fachübergreifendes und praxisnahes Lernen : Das ist das Ziel des didaktischen Projekts für die Masterstudiengänge Volkswirtschaftslehre, Economics und Mathematik. Studierende aus unterschiedlichen Disziplinen sollen gemeinsam Lösungen für Probleme aus der Praxis erarbeiten und umsetzen. Dabei arbeiten sie in fachübergreifenden Kleingruppen an verschiedenen Projekten, die teilweise in Kooperation mit Banken und Versicherungen entwickelt werden. Hierdurch wird einerseits eine dem späteren Berufsalltag nachempfundene Situation hergestellt und andererseits die praktische Anwendungskompetenz von im Studium erworbenen Kenntnissen gezielt gefördert.

Die Ergebnisse der verschiedenen Projekte sollen von den Teilnehmerinnen und Teilnehmern regelmäßig im Kurs präsentiert werden und gegenseitig ausgewertet werden. Durch die stark interdisziplinäre und projektbasierte Arbeitsweise an praxisrelevanten Aufgaben will das Konzept die Studierenden zum Selbststudium anregen und intensiv auf die spätere Berufswelt vorbereiten.

Das Seminar wird im WS 2017/18 stattfinden und beinhaltet die über 4×4 Wochen gehende Bearbeitung von kleineren Projekten in interdisziplinären Teams aus 4 Personen. Die Themen werden von Praxispartnern gestellt und etwaige Spezialkenntnisse vorab in einem Blockkurs vermittelt. Im Anschluss können möglicherweise Themen weiter verfolgt werden, wie etwa in einer Masterarbeit oder einem Praktikum.

Eine Anmeldung ist unbedingt erforderlich, siehe Homepage !____________________________________

Inhalt:
 
Das Wachstum des World Wide Webs und das Hervorkommen von and Online-Netzwerkgemeinschaften wie Facebook oder LinkedIn haben das Interesse am Studium von Netzwerkdaten erheblich intensiviert. In dem Seminar besprechen wir mathematische Grundlagen statistischer Netzwerkanalyse. Dabei werden wir aktuelle Artikel studieren und diskutieren. Die ersten Vorträge stellen allgemeine probabilistische Resultate insbesondere zum Erdös-Renyi-Modell bereit.

Die parallele Vorlesung Mathematische Statistik¨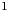st für die Bereitstellung allgemeiner statistischer Theorie sehr empfehlenswert. Eine intensive Mitarbeit und ein fundierter mathematischer Hintergrund in der Stochastik werden für die Teilnahme vorausgesetzt.

Die Literatur wird in der Vorbesprechung vorgestellt._______________________________________________

Inhalt:
 
Wir werden uns mit der Beschreibung von stochastischen Prozessen auf Mannigfaltigkeiten mit Hilfe von stochastischen Differentialgleichungen, Martingalproblemen und Markovschen Halbgruppen beschäftigen. Dies ist ein fortgeschrittenes, jedoch gut verstandenes Thema. Die geometrische Sichtweise ermöglicht ein vertieftes Verständnis der Theorie stochastischer Prozesse (Invarianzresultate, asymptotische Entwickungen der Dichte, etc.). Umgekehrt ermöglichen stochastische Methoden neue Sichtweisen auf geometrische Fragestellungen (stochastische Darstellung von Lösungen partieller Differentialgleichungen und von geometrischen Flüssen, Transportprobleme, Indexsatz von Atiyah–Singer, etc.). Je nach Zeit und Interesse werden wir auf einige Anwendungen eingehen (Asymptotik von Optionspreisen, Existenz endlichdimensionaler Realisierungen von Zinsmodellen, Stochastik auf Räumen von geometrischen Figuren und weitere Themen nach Wahl).

Literatur:

1.)

E. P. Hsu (2002), Stochastic Analysis on Manifolds. American Mathematical Society, Providence, RI.

2.)

D. W. Stroock (2000), An introduction to the analysis of Paths on a Riemannian Manifold. American Mathematical Society, Providence, RI.

3.)

W. Hackenbroch and A. Thalmaier (1994), Stochastische Analysis. B. G. Teubner, Stuttgart.

Inhalt:
Zur Beantwortung komplexer biomedizinischer Fragestellungen aus großen Datenmengen ist oft ein breites Spektrum an Analysewerkzeugen notwendig, z.B. Deep Learning- oder allgemeiner Machine Learning-Techniken, was häufig unter dem Begriff „Medical Data Science“ zusammengefasst wird. Statistische Ansätze spielen eine wesentliche Rolle als Basis dafür. Eine Auswahl von Ansätzen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren. Die genaue thematische Ausrichtung wird noch festgelegt. Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik dienen.

Vorbesprechung mit Hinweisen auf einführende Literatur :
Mittwoch den 19.07.2017, 10 :30–11 :30 Uhr, Konferenzraum Institut für Medizinische Biometrie und Statistik, Stefan-Meier-Str. 26, 1. OG

Vorherige Anmeldung per E-Mail (sec@imbi.uni-freiburg.de) ist erwünscht.___________

Inhalt:
In der Mathematik bezeichnet man durch Eichtheorie Beschreibungen von Strukturen auf Vektor- sowie Hauptfaserbündeln. In Rahmen dieses Seminars werden wir uns hauptsächlich mit Seiberg-Witten Eichtheorie beschäftigen, die Einsicht in Topologie und Geometrie von 4-Mannigfaltigkeiten liefert. Zum Beispiel, mit Hilfe der Seiberg-Witten Eichtheorie kann man zeigen, dass es glatte 4-Mannigfaltigkeiten existieren, die homöomorph aber nicht diffeomorph sind. Sofern die Zeit erlaubt, werden wir auch einen Blick auf die Theorie von Donaldson werfen, die auch viele Anwendungen in der Topologie von 4-Mannigfaltigkeiten hat.________________________________________________________________________________________________________________

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden ; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf ; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann.

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe (einem Oberseminar, Projektseminar …)) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im Vertiefungsmodul gibt es eine mündliche Abschlussprüfung über den Stoff des Lesekurses und den weiteren Stoff des Moduls.____________________________________________

Inhalt:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in Geometry” : algebraic geometry, arithmetic geometry, representation theory, differential topology or mathematical physics or a mix thereof.

The precise topic will be chosen at the end of the preceeding semester. The program will be made available via our web site.

The level is aimed at our doctoral students. Master students are very welcome to participate as well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. A. Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________

Inhalt:
The Joint Seminar is a research seminar in complex and algebraic geometry, organized by the research groups in Freiburg, Nancy and Strasbourg. The seminar meets roughly twice per semester in Strasbourg, for a full day. There are about four talks per meeting, both by invited guests and by speakers from the organizing universities. We aim to leave ample room for discussions and for a friendly chat.

The talks are open for everyone. Contact one of the organizers if you are interested in attending the meeting. We have some (very limited) funds that might help to support travel for some junior participants.____________________________________________________________________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17 :00 Uhr im Hörsaal II in der Albertstr. 23 b statt.

Vorher gibt es um 16 :30 Uhr im Sozialraum 331 in der Eckerstraße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/