Lehrveranstaltungen

Inhalt:
 
Die Vorlesung führt in die stochastische Denkweise ein und erläutert Begriffe, Techniken und Resultate der Wahrscheinlichkeitstheorie. Grundlegend sind hierbei diskrete und stetige Wahrscheinlichkeitsverteilungen sowie Zufallsvariablen. Zunächst starten wir mit einer präzisen Definition von Wahrscheinlichkeiten, Zufallsvariablen, Dichten und lernen die zugehörigen Techniken kennen. Danach werden zentrale Resultate wie das Gesetz der großen Zahlen und der zentralen Grenzwertsatz eingeführt. Schließlich wird eine kurze Einführung in die parametrische statistische Testtheorie Maximum-Likelihood-Schätzer und Hypothesentests behandeln.

Die Vorlesung wird im SS 2016 durch eine weitere 2-stündige Vorlesung fortgesetzt, dann wird es auch Praktische Übungen zur Stochastik geben.

Der Stoff der Vorlesung kann als Prüfungsstoff für Staatsexamensprüfungen herangezogen werden.

Literatur:

1.)

Krengel, U. : Einführung in die Wahrscheinlichkeitstheorie und Statistik. Vieweg, 1988

2.)

Georgii, H. O. : Stochastik : Einführung in die Wahrscheinlichkeitstheorie und Statistik. de Gruyter, 2002

3.)

Czado, C. und T. Schmidt : Mathematische Statistik. Springer, 2011. (Nur für den statistischen Teil)

Inhalt:
Die Numerik ist eine Teildisziplin der Mathematik, die sich mit der praktischen Lösung mathematischer Aufgaben beschäftigt. Dabei werden Probleme in der Regel nicht exakt sondern approximativ gelöst. Typische Beispiele sind die Bestimmung von Nullstellen einer Funktion oder die Lösung linearer Gleichungssysteme. In der Vorlesung werden einige grundlegende numerische Algorithmen vorgestellt und im Hinblick auf Rechenaufwand sowie Genauigkeit untersucht. Die Vorlesung ist der erste Teil eines zweisemestrigen Kurses. Der Besuch der begleitenden praktischen Übungen wird empfohlen. Diese finden 14-täglich im Wechsel mit der Übung zur Vorlesung statt.

Literatur:

1.)

R. Plato : Numerische Mathematik kompakt. Vieweg, 2006.

2.)

R. Schaback, H. Wendland : Numerische Mathematik. Springer, 2004.

3.)

J. Stoer, R. Burlisch : Numerische Mathematik I, II. Springer, 2007, 2005.

4.)

G. Hämmerlin, K.-H. Hoffmann : Numerische Mathematik. Springer, 1990.

5.)

P. Deuflhard, A. Hohmann, F. Bornemann : Numerische Mathematik I, II. DeGruyter, 2003.

Inhalt:
In der linearen Algebra ging es um das Lösen von linearen Gleichungssystemen. Gegen- stand der Vorlesung “Algebra und Zahlentheorie” ist das Lösen von Polynomgleichungen in einer Variablen. Aus der Schule bekannt ist der Fall quadratischer Gleichungen und deren Lösungsformel. Eines unserer Hauptresultate wird es sein, dass sich diese Lösungsformel nicht verallgemeinern lässt. Verwandt ist die Frage nach der Konstruierbarkeit von geometrischen Figuren mit Zirkel und Lineal.

Unser wesentliches Hilfsmittel ist die Theorie der algebraischen Körpererweiterungen mit dem Hauptsatz der Galoistheorie als Höhepunkt. Auf dem Weg werden wir auch andere algebraische Strukturen wie Gruppen und Ringe studieren. Von besonderem Interesse ist der Fall von Gleichungen über den rationalen oder gar ganzen Zahlen. Dies ist Gegenstand der Zahlentheorie.

Literatur:

1.)

Michael Artin : Algebra

2.)

Siegfried Bosch, Algebra

3.)

Serge Lang, Algebra

Inhalt:
Das mehrdimensionale Riemann-Integral ist eine direkte Verallgemeinerung des Riemann-Integrals aus der Analysis-Vorlesung. Es erlaubt, stetige Funktionen über geeignete „einfache“ kompakte Gebiete im ℝⁿ zu integrieren. Wir beweisen in diesem Kontext den Satz von Fubini und die Transformationsformel, mit deren Hilfe sich diese Integrale oft auf mehrere eindimensionale Integrale zurückführen lassen. Außerdem führen wir Oberflächenintegrale ein und lernen elementare Formen der Integralsätze von Stokes und Gauß kennen.

Literatur:

1.)

W. Walter, Analysis 2, 5. erw. Aufl., Springer, Berlin, 2002

Inhalt:
Grundlagen der Maßtheorie : Maße, Fortsetzungssatz, Lebesgue-Integral, Konvergenzsätze, Fubini ; Integration im ℝⁿ : Lebesgue-Maß, Transformationssatz, Untermannigaltigkeiten und Oberflächenintegrale, Satz von Gauß, Satz von Stokes, Fouriertransformation.

Literatur:

1.)

H. Bauer, Wahrscheinlichkeitstheorie und Grundzüge der Maßtheorie. 3. Auflage, de Gruyter, 1978

2.)

J. Elstrodt, Maß- und Integrationstheorie, Springer, 2007

3.)

H. Amann, J. Escher, Analysis III, Birkhäuser, 2001

4.)

W.H. Fleming, Functions of several variables, Springer, 1977

5.)

H.W. Alt, Lineare Funktionalanalysis, Springer, 2002. Hierin die Kapitel über die Lebesgue-Räume.

6.)

W. Soergel, Analysis 3, http://home.mathematik.uni-_freiburg.de/soergel/#Skripten

Inhalt:
Die Aufgabe der Wahrscheinlichkeitstheorie ist es, zufallsabhängige Vorgänge mathematisch zu beschreiben. Die Vorlesung ist eine systematische Einführung dieses Gebietes auf maßtheoretischer Grundlage.

Ziel der Vorlesung ist es, Methoden der stochastischen Modellbildung und Analyse zu entwickeln und einige der klassischen Grenzwertsätze herzuleiten. Vorkenntnisse aus der Vorlesung Analysis III sind hilfreich, jedoch nicht Voraussetzung.

Literatur:

1.)

Klenke, A. : Wahrscheinlichkeitstheorie, Springer 2008

2.)

Kallenberg, O. : Foundations of Modern Probability, Springer 2002

3.)

Williams, D. : Probability with Martingales, Cambridge University Textbooks, 1991

4.)

Hesse, Ch. : Angewandte Wahrscheinlichkeitstheorie, Vieweg, Januar 2003

Inhalt:
Diese Vorlesung ist die erste eines Kurses von aufeinander aufbauenden Vorlesungen zur Theorie und Numerik partieller Differentialgleichungen.

Partielle Differentialgleichungen treten oft als Modelle für physikalische Vorgänge auf, z.B. bei der Bestimmung einer Temperaturverteilung, bei der Beschreibung von Schwingungen von Membranen oder Strömungen von Flüssigkeiten.

In dieser Vorlesung werden wir uns mit elliptischen Differentialgleichungen beschäftigen. Es wird sowohl die klassische Existenztheorie, als auch die moderne Theorie zur Lösbarkeit solcher Gleichungen behandelt. Selbst wenn man für einfache Probleme explizite Lösungsformeln hat, können diese nur selten auch konkret berechnet werden. Deshalb ist es wichtig numerisch approximative Lösungen zu berechnen und nachzuweisen, dass diese in geeigneter Weise gegen die exakte Lösung konvergieren. Dazu wird in der Vorlesung die entsprechende Theorie Finiter Elemente dargestellt.

Parallel zu der Vorlesung wird eine Praktische Übung (siehe Kommentar zur Praktischen Übung) angeboten.

Literatur:

1.)

Evans, Partial Differential equations, AMS (1998).

2.)

Braess, Finite Elemente, Springer (1992).

3.)

Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010).

Inhalt:
Wir beginnen mit der Vorstellung der Axiome der Mathematik. Sie prägen unsere Auffassung von den möglichen definierbaren oder vielleicht weniger konstruktiv gegebenen mathematischen Objekten. Allerdings zeichnen sie kein vollständiges Bild eines einzigen mathematischen Universums. Die Liste der herleitbaren mathematischen Aussagen ist unvollständig : Für manche φ ist weder φ noch sein Negat aus den Zermelo-Fraenkel’schen Axiomen ZFC beweisbar. Man sagt “φ ist unabhängig von ZFC”.

Die Vorlesung führt in die Technik der Unabhängigkeitsbeweise ein. Wir stellen Gödels inneres Model L und die ersten Schritte des Forcing vor.

Die bekannteste von ZFC unabhängige Aussage ist die Kontinuumshypothese, die sagt, dass es genau ℵ₁ reelle Zahlen gibt.

Literatur:

1.)

H.-D. Ebbinghaus, Einführung in die Mengenlehre. 4. Auflage, 2003.

2.)

L. Halbeisen, Combinatorial Set Theory. With a Gentle Introduction to Forcing, 2012

3.)

Thomas Jech, Set Theory. The Third Millenium Edition, 2001.

4.)

Kenneth Kunen, Set Theory, An Introduction to Independence Proofs. 1980.

5.)

Kenneth Kunen, Set Theory. Second Edition, 2013.

Inhalt:
Die Modelltheorie untersucht den Zusammenhang zwischen mathematischer Syntax und Semantik, d. h. zwischen der Art, wie mathematische (hier vor allem : algebraische) Eigenschaften in formaler Sprache ausgedrückt werden, und dem Verhalten ihrer Modelle.

Ein offensichtliches Beispiel eines solchen Zusammenhangs liefert die Beobachtung, dass universelle (d. h. durch Allquantoren ausdrückbare) Eigenschaften von Strukturen auf ihre Unterstrukturen übergehen. Es gilt aber auch die Umkehrung : Unter Unterstrukturen abgeschlossene Modellklassen sind durch universelle Eigenschaften axiomatisierbar.

Die Vorlesung soll bis zu den Sätzen von Morley und Baldwin-Lachlan kommen, die eine Strukturtheorie für sogenannte ℵ₁-kategorische Theorien entwickeln, die die aus der Linearen Algebra bekannte Dimensionstheorie von Vektorräumen verallgemeinert : K-Vektorräume sind bis auf Isomorphie durch ihre Dimension charakterisiert. Ein anderes Beispiel sind algebraisch abgeschlossene Körper fester Charakteristik, die bis auf Isomorphie durch ihren Transzendenzgrad bestimmt sind.

Die Vorlesung setzt einige Kenntnisse aus der formalen Logik voraus, die zu Beginn rasch wiederholt werden. Sie kann ohne vorausgehende „Mathematische Logik“ gehört werden, wenn man bereit ist, sich diese Logik-Grundlagen im Selbststudium anzueignen. Beispiele kommen meistens aus der Algebra und setzen vereinzelt algebraische Kenntnisse voraus.

Literatur:

1.)

M. Ziegler : Skript „Modelltheorie“, 2001.
home.mathematik.uni-_freiburg.de/ziegler/skripte/

2.)

K. Tent, M. Ziegler : “A course in model theory”, Association of Symbolic Logic 2012.

3.)

W. Hodges : “Model Theory”, Cambridge University Press 1993

Inhalt:

Zunächst werden differenzierbare Mannigfaltigkeiten, Vektorfelder und allgemeine Tensorfelder eingeführt. Das sind grundlegende Begriffe der Differentialgeometrie, die auch in der Analysis und der Physik wichtig sind. Darauf aufbauend wird eine Einführung in das größte Teilgebiet der Differentialgeometrie, die Riemannsche Geometrie, gegeben. Insbesondere werden Geodätische und der Riemannsche Krümmungstensor eingeführt und die geometrische Bedeutung des Riemannschen Krümmungstensors erklärt.

Literatur:

1.)

J.M. Lee : Introduction to Smooth Manifolds. Springer (GTM 218), 2003

2.)

M.P. do Carmo : Riemannian Geometry. Birkhäuser, Boston 1992

3.)

J.M. Lee : Riemannian Manifolds. An Introduction to Curvature. Springer (GTM 176), 1997

Inhalt:
Gegenstand der Vorlesung ist die mehrdimensionale Variationsrechnung. Wir betrachten Funktionale bzw. Variationsintegrale der Form

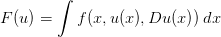
Literatur:

1.)

Struwe, Michael, Variational Methods. Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 4th edition. Springer-Verlag, Berlin, 2008.

2.)

Giaquinta, Mariano, Multiple integrals in the calculus of variations and nonlinear elliptic systems. Annals of Mathematics Studies, 105. Princeton University Press, 1983.

Inhalt:
Grundlegende Probleme der statistischen Entscheidungtheorie sind das Schätzen von Parametern eines statistischen Modells sowie Hypothesentests. Aufbauend auf der Vorlesung Wahrscheinlichkeitstheorie werden die wichtigsten Begriffe und Methoden der Mathematischen Statistik erarbeitet. Dabei wird sowohl Wert auf die Theorie als auch auf in Anwendungen häufig auftretende Verfahren gelegt.

Stichworte : Bayes’sche Statistik, Klassifizierung, Lebenszeitanalyse, Likelihood Ratio Test, Maximum Likelihood, Multiples Testen, Principle Component Analyse, Regression, Regularisierung, Resampling-Methoden, Varianzanalyse, Zeitreihe.

Literatur:

1.)

C. Czado und T. Schmidt, Mathematische Statistik (Statistik und ihre Anwendungen), Springer, 2011

2.)

T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning : Data Mining, Inference, and Prediction, Springer, 2011

3.)

L. Rüschendorf, Mathematische Statistik, Springer 2014

Inhalt:
Die Vorlesung ist die erste Veranstaltung im Studiengang Master of Science Mathematik, Studienschwerpunkt Wahrscheinlichkeitstheorie, Finanzmathematik und Statistik, insbesondere in der neuen Profillinie Finanzmathematik. Sie schließt direkt an die Vorlesung Wahrscheinlichkeitstheorie aus dem WS 2014/15 an.

Ein stochastischer Prozess (X_t)_t≥0 ist eine Familie von Zufallsvariablen. Einfache Beispiele sind Irrfahrten, Markov-Ketten, die Brown’sche Bewegung oder davon abgeleitete Prozesse. Vor allem in der Modellierung von finanzmathematischen oder naturwissenschaftlichen Fragestellungen spielt die Brownsche Bewegung eine große Rolle.

Wir werden uns zunächst mit der reichhaltigen Klasse von Martingalen beschäftigen und die wichtigen Martingalkonvergenzsätze kennen lernen. Anschließend konstruieren wir die Brown’sche Bewegung und studieren ihre Pfadeigenschaften. Infinitesimale Charakteristiken eines Markov-Prozesses werden durch Generatoren beschrieben, was eine Verbindung zur Theorie von partiellen Differentialgleichungen ermöglicht.

Im Sommersemester 2016 wird diese Veranstaltung durch die Vorlesung Stochastische Integration und Finanzmathematik fortgeführt.

Literatur:

1.)

O. Kallenberg. Foundations of Modern Probability (Probability and Its Applications). Springer 2002

2.)

A. Klenke. Wahrscheinlichkeitstheorie. Springer 2006

3.)

D. Williams. Probability with Martingales (Cambridge Mathematical Textbooks). Cambridge University Press 1991

Inhalt:
Viele Phänomene in der Natur lassen sich durch mathematische Modelle, insbesondere durch partielle Differentialgleichungen, beschreiben. Die wichtigsten unter diesen sind die elliptischen, die parabolischen und die hyperbolischen Differentialgleichungen. Gesucht werden jeweils Funktionen mehrerer Veränderlicher, deren Ableitungen gewisse Gleichungen erfüllen.

Eine besondere Klasse von partiellen Differentialgleichungen bilden die hyperbolischen Erhaltungssätze. Trotz beliebig glatter Daten (damit sind Randwerte, Anfangswerte und die Koeffizienten gemeint) können die zugehörigen Lösungen unstetig sein. Ihre Behandlung ist daher eine besondere Herausforderung an die Analysis und die Numerik.

Diese Differentialgleichungen sind z.B. mathematische Modelle für Strömungen kompressibler Gase und für verschiedene Probleme aus den Bereichen Astrophysik, Grundwasserströmungen, Meteorologie, Halbleitertechnik und reaktive Strömungen. Beispielsweise ist das mathematische Modell für eine Supernova von derselben Struktur wie das für die Verbrennung in einem Fahrzeugmotor. Kenntnisse in diesen Bereichen werden aber nicht vorausgesetzt. In der Vorlesung sollen die theoretischen Grundlagen geschaffen werden, um Simulationen der oben genannten Probleme am Computer durchzuführen.

Literatur:

1.)

D. Kröner, Numerical Schemes for Conservation Laws, Wiley und Teubner, Chichester, Stuttgart (1997)

2.)

R.J. LeVeque, Numerical Methods for Conservation Laws, Birkhäuser Verlag, Basel (1992)

3.)

R.J. LeVeque, Finite Volume Methods for Hyperbolic Problems, Cambridge Texts in Applied Mathematics (2002)

Inhalt:
Im ersten Teil dieser Vorlesung betrachten wir analytische und numerische Methoden um parabolische partielle Differentialgleichungen zweiter Ordnung, also natürliche Verallgemeinerungen der Wärmeleitungsgleichung, zu behandeln. Wir zeigen insbesondere Existenz und Eindeutigkeit, sowie Regularität, von schwachen Lösungen solcher Gleichungen und entwickeln darauf aufbauend numerische Verfahren.

Im zweiten Teil behandeln wir nichtlineare elliptische Variationsprobleme und deren Gradientenflüsse. Ein besonderer Fokus in diesem Teil liegt in Modellen aus der Elastizitätstheorie und in Modellen, bei denen ein Grenzübergang mit einem kleinen Parameter auftritt. Am Beispiel der Modica-Mortola-Energie lernen wir hier die analytische Methode der Gamma-Konvergenz kennen.

Literatur:

1.)

L.C. Evans : Partial Differential Equations (2nd edition). American Mathematical Society 2010.

2.)

D. Braess : Finite Elemente : Theorie, schnelle Löser und Anwendungen in der Elastizitätstheorie. Springer 2013.

3.)

V. Thomee : Galerkin finite element methods for parabolic problems. Springer 2010.

4.)

A. Braides : Gamma-Convergence for Beginners. Oxford University Press 2002.

Inhalt:
The course’s aim is to give an introduction into numerical methods for the solution of optimization problems in science and engineering. The focus is on continuous nonlinear optimization in finite dimensions, covering both convex and nonconvex problems. The course is accompanied by intensive computer exercises and divided into four major parts :

1.

Fundamental Concepts of Optimization : Definitions, Types, Convexity, Duality

2.

Unconstrained Optimization and Newton Type Algorithms : Stability of Solutions, Gradient and Conjugate Gradient, Exact Newton, Quasi-Newton, BFGS and Limited Memory BFGS, and Gauss–Newton, Line Search and Trust Region Methods, Algorithmic Differentiation

3.

Equality Constrained Optimization Algorithms : Newton Lagrange and Generalized Gauss-Newton, Range and Null Space Methods, Quasi-Newton and Adjoint Based Inexact Newton Methods

4.

Inequality Constrained Optimization Algorithms : Karush-Kuhn-Tucker Conditions, Linear and Quadratic Programming, Active Set Methods, Interior Point Methods, Sequential Quadratic and Convex Programming, Quadratic and Nonlinear Parametric Optimization

Literatur:

1.)

Jorge Nocedal and Stephen J. Wright, Numerical Optimization, Springer, 2006

2.)

Amir Beck, Introduction to Nonlinear Optimization, MOS-SIAM Optimization, 2014

3.)

Stephen Boyd and Lieven Vandenberghe, Convex Optimization, Cambridge Univ. Press, 2004

Inhalt:
Eine naheliegende Verallgemeinerung von Funktionen f : I ⊂ ℝ → ℝ sind Funktionen u : I → B mit Werten in einem allgemeinen Banachraum B. Bochner-Räume L^p(I,B) können zunächst als Abstraktion der in Analysis III definierten Lebesgue-Räume L^p(I, ℝ) aufgefasst werden. Es zeigt sich aber andererseits auch, dass Bochner-Räume den geeigneten Rahmen für die mathematische Behandlung einer Vielzahl instationärer partieller Differentialgleichungen bilden. Exemplarisch seien die Navier-Stokes-Gleichungen aus der Theorie inkompressibler, viskoser Flüssigkeiten erwähnt, deren mathematische Behandlung sicheren Umgang mit Bochner-Räumen verlangt.
Wir wollen in dieser Vorlesung daher grundlegende Techniken und Resultate wie z. B. Bochner-Meßbarkeit, Dualräume, vektorwertige Distributionen, die partielle Integrations-Formel oder das Kompaktheitslemma von Aubin und Lions erarbeiten. Geplant ist außerdem, dass parallel zur Vorlesung ein Skript entsteht.
Die Vorlesung richtet sich besonders an Studenten, die eine Bachelor- oder Masterarbeit in einem Bereich der angewandten Mathematik planen.

Literatur:

1.)

Michael Růžička, Nichtlineare Funktionalanalysis, Springer, 2004

2.)

Etienne Emmrich, Gewöhnliche und Operator-Differentialgleichungen, Vieweg+Teubner, 2004

3.)

H. Gajewski, K. Gröger. K. Zacharias, Nichtlineare Operatorgleichungen, Akademie-Verlag, 1974

Inhalt:
In this course, we first give a concise introduction to the R programing environment (for students of mathematics, this may be a refreshment of some material they already encountered in the practical exercises accompanying the lecture “Stochastik”). With help of the provided tools, we then develop some programs for bootstrapping zero rates, pricing vanilla options in binomial trees and exotic options in time-continuous models via Monte Carlo methods. We also regard some aspects of hedging and convergence in this context. Further we discuss the implementation of risk measures, the sampling of loss distributions in elementary credit risk models. Depending on the time left, we may additionally discuss the simulation of (approximate) solutions to stochastic differential equations.
The course, which is taught in English, is offered for the second year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. (possibly also B.Sc.) Mathematics (can be credited as “Wahlmodul” in both M.Sc. and B.Sc. Mathematics, and in particular for students of the profile “Finanzmathematik” in M.Sc. Mathematics as specialization in economics).

Literatur:

1.)

Hull, J.C. : Options, Futures, and other Derivatives, 7th ed., Prentice Hall, 2009

2.)

Lai, T.L., Xing, H. : Statistical Models and Methods for Financial Markets, Springer, 2008

3.)

Seydel, R.U. : Tools for Computational Finance, 4th ed., Springer, 2009

4.)

Any introductory book to the R programming environment, e.g.,
Brown, J., Murdoch, D.J. : A First Course in Statistical Programming with R, Cambridge University Press, 2007

Inhalt:
Credit risk represents by far the biggest risk in the activities of a traditional bank. In particular, during recession periods financial institutions loose enormous amounts of money as a consequence of bad loans and default events. In the last two decades, a multitude of credit-linked derivatives has been developed to manage and transfer credit risks in an efficient and standardized way. These allow banks to shape their risk profile according to regulatory standards.

In this lecture, we introduce some of the most popular single name- and portfolio credit models and show how these are used to measure credit risk and to price credit derivatives like credit default swaps (CDS), basket default swaps and defaultable bonds. We will also introduce different measures of credit risk and will discuss concentration risk in credit portfolios.

The course, which is taught in English, is offered for students in the Finance profile of the M.Sc. Economics, but is also open to students of M.Sc. Volkswirtschaftslehre and M.Sc. Mathematics, especially to those of the profile “Finanzmathematik”.

Literatur:

1.)

Bielecki, T.R., Rutkowski, M. : Credit Risk : Modeling, Valuation, and Hedging. Springer, 2002

2.)

Bluhm, C., Overbeck, L. : Structured credit portfolio analysis, baskets & CDOs. Chapman & Hall/CRC Press, 2006

3.)

Duffie, D., Singleton, K.F. : Credit Risk : Pricing, Measurement, and Management. Princeton University Press, 2003

4.)

Lando, D. : Credit Risk Modeling : Theory and Applications. Princeton University Press, 2004

5.)

Lütkebohmert, E. : Concentration Risk in Credit Portfolios. Springer, 2009

6.)

Schönbucher, P.J. : Credit Derivatives Pricing Models. Wiley, 2003

Inhalt:
In der Differentialtopologie werden globale geometrische Invarianten topologischer Räume, die zusätzlich eine differenzierbare Struktur besitzen, gesucht und untersucht. Wir werden mit der Brouwerschen Definition des Abbildungsgrades und regulären Werten einsteigen und uns bis zu gerahmten Kobordismen vorarbeiten.

Die Vorlesung soll einen elementaren und intuitiven Einstieg in die Differentialtopologie ermöglichen und wird ausschließlich mit Untermannigfaltigkeiten arbeiten, also mit expliziten Einbettungen von Mannigfaltigkeiten in den euklidischen Raum. Damit ist die Vorlesung sowohl begleitend/anschließend zur Differentialgeometrie oder algebraischen Geometrie geeignet als auch für Hörer ohne diese Vorkenntnisse.

Literatur:

1.)

J. Milnor, Topology from the differentiable viewpoint, University Press of Virginia, 1965

2.)

V. Guillemin und A. Pollack, Differential topology, Prentice-Hall, 1974

Inhalt:
The group SL₂(ℝ) acts on the upper half plane ℍ = {z ∈ ℂ | Im(z) > 0} by fractional linear transformations, yielding an isomorphism Aut(ℍ)SL₂(ℝ)∕{±1}. Let Γ be a subgroup of SL₂(ℤ) defined by congruence conditions. The quotients Γ\ℍ, more precisely, certain disjoint unions X of them, are the easiest examples of Shimura varieties. The following observations can be made :

1. X is an algebraic variety, canonically defined over ℚ (sometimes even over ℤ). It is the solution to a moduli problem for elliptic curves with level structures.

2. There are canonical line bundles on the Xs, whose sections are precisely the modular forms.

3. X can be naturally compactified.

4. There are distinguished points on the Xs, the so called CM-points (complex multiplication), where the Galois action can be described explicitly in terms of class field theory. There are sufficiently many of those to characterize the ℚ-models of the Xs uniquely.

5. There is a huge ring of correspondences, the so called Hecke algebra, acting on X and the modular forms. It can be used to reveal a deep connection between modular forms and 2-dimensional Galois representations.

All these facts have analogues for ℍ replaced by an arbitrary Hermitian symmetric domain D and for Γ replaced by a subgroup of G(ℤ) defined by congruence conditions. Here G is a linear algebraic group defined over ℤ (semi-simple over ℚ) with a surjective homomorphism with compact kernel

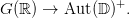
There will be two appointments per week. One will be used for the lecture, and the other for discussing exercises, providing background material (e.g. on linear algebraic groups, Abelian varieties, class field theory, etc.).

Literatur:

1.)

Milne, J. S. ; Introduction to Shimura varieties., available at http ://www.jmilne.org/math/

2.)

Deligne, Pierre ; Travaux de Shimura. (French) Séminaire Bourbaki, 23ème année (1970/71), Exp. No. 389, pp. 123–165.

Inhalt:

Frank Knight (1921) remarks that “The practical difference between risk and uncertainty is that in the former the distribution of the outcome in a group of instances is known (either through calculation a priori or from statistics of past experience), while in the case of uncertainty this is not true”. In this course, we will discuss the theory of model uncertainty (also known as G-stochastic calculus) as introduced by Shige Peng. What drew much attention to the study of G-stochastic calculus in the first place is a novel notion of coherent risk measures known as the G-expectation. The G-expectation and its corresponding canonical process, the G-Brownian motion can be seen as the central objects of the G-stochastic calculus.
This course, which is taught in English, is offered for students of the profile Finanzmathematik.

Literatur:

1.)

Peng, S. :
Nonlinear Expectations and Stochastic Calculus under Uncertainty. Preprint, 2010.

2.)

Fadina, T. R. :
Nonstandard Analysis for G-Stochastic Calculus. Bielefeld University, 2015.

Inhalt:
In dieser Vorlesung wird die stochastische Integration im endlichdimensionalen Fall für allgemeine Semimartingale eingeführt. Auf der einen Seite ist dies die größte Klasse von Prozessen, für die sich eine stochastische Analysis gut betreiben lässt, auf der anderen Seite sind dies auch genau die Prozesses, die nach dem FTAP zu arbitragefreien Märkten führen.

Die Vorlesung vertieft die Inhalte der Vorlesung Stochastische Prozesse und führt sie auf einem höheren Level fort. Die Vorlesung kann auch auf Englisch gehalten werden.

The first two lectures will be given by Monique Jeanblanc, who will give an introductory course on enlargement of filtrations in discrete time. Prof. Jeanblanc is one of the leading experts in this topic, so this will be a good starting point for the following lectures. (These lectures will be in English.)

The lectures will be in English on request.

We will start with a detailed look into the theory of semimartingale processes. The focus will be on the important proofs, and other parts will be left as exercise. The course is intended for students with a strong background in probability.

Literatur:

1.)

Jacod/Shiryaev : Limit Theorems for Stochastic Processes

2.)

Bichteler : Stochastic Integration and L^p-Theory of Semimartingales, Ann. Probab. 9 (1981) 49–89

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden im BSc- oder MSc-Studiengang Mathematik, die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Leistungsnachweis :

• Teilnahme an der Einführungsveranstaltung (voraussichtlich in der ersten Vorlesungswoche ; Termin wird kurzfristig im Vorlesungsverzeichnis bekanntgegeben)
• regelmäßige Teilnahme an der Tutorenbesprechung
• zwei gegenseitige Tutoratsbesuche mit einem anderen Modulteilnehmer, welcher nach Möglichkeit die gleiche Vorlesung tutoriert, oder zwei Besuche durch den betreuenden Assistenten und Austausch über die Erfahrungen (die Zuteilung der Paarungen erfolgt bei der Einführungsveranstaltung)
• Schreiben eines Erfahrungsberichts, der an den betreuenden Dozenten geht

In Ermangelung eines passenden Wahlbereichs kann das Modul für Lehramtsstudierende in dieser Form zur Zeit nicht angeboten werden.__________________________________________________________

Inhalt:
Die Vorlesungen über Didaktik bestehen aus zwei Teilen : Didaktik der Algebra und Analysis (WS) und Didaktik der Geometrie und Stochastik (SS).

Eine scharfe Abgrenzung der Einzelthemen ist im schulischen Kontext wenig hilfreich. So wird z.B. die Projektion auf den ersten Blick der Geometrie zugeordnet, andererseits entsteht durch die Projektion einer Drehbewegung die Sinus- bzw. Kosinusfunktion. Im Sinne einer ganzheitlichen und vernetzenden Didaktik werden in der Vorlesung viele Bezüge zwischen den einzelnen, innermathematischen Disziplinen geschaffen.

Erörtert werden didaktische Methoden der Geometrie und Stochastik, die didaktische Bedeutung des Materials im schulischen Kontext sowie die Bedeutung von kooperativem Lernen (Gruppenarbeit). Zentral ist der Wechsel zwischen symbolischen, ikonischen und enaktiven Repräsentationsebenen (nach Bruner). An konkreten Beispielen wird ein konstruktivistischer Vermittlungsansatz im Kontext der bildungsplanspezifischen Inhalte (lernen, begründen, problemlösen und kommunizieren) aufgezeigt.
Die Vorlesung legt Wert darauf, dass die dargestellte Didaktik konkret und interaktiv erlebt wird. Die Folge ist ein ständiger Rollenwechsel des Hörers : Einerseits erlebt er die Dinge aus der Schülerperspektive, auf der anderen Seite schlüpft er in die Rolle des reflektierenden Lehrers.

Literatur:

1.)

Bauer, J. : Warum ich fühle, was Du fühlst ; Hoffmann und Campe

2.)

Eichler A. ; Vogel M. : Leitidee Daten und Zufall : Von konkreten Beispielen zur Didaktik der Stochastik ; Wiesbaden : Vieweg + Teubner, 2009

3.)

Henn, J. : Geometrie und Algebra im Wechselspiel : Mathematische Theorie für schulische Fragestellungen ; Springer Spektrum, 2012

4.)

Kramer, M. : Mathematik als Abenteuer ; Aulis Verlag

5.)

Kramer, M. : Schule ist Theater ; Schneider-Verlag Hohengehren

6.)

Spitzer, M. : Geist im Netz – Modelle für Lernen, Denken und Handeln ; Spektrum Akademischer Verlag, Heidelberg

7.)

Thun, S. v. : Miteinander Reden, Bd. I–III ; Rowohlt Tb.

Inhalt:
MINT steht für die Vernetzung von Mathematik, Informatik, Naturwissenschaft und Technik. Der erste Buchstabe steht für Mathematik, jedoch vereint Robotik alle ( !) vier Buchstaben gleichzeitig und eignet sich exemplarisch für die Schule, sowohl im Rahmen einer AG, von Projekttagen oder im Unterricht.

Das Seminar besteht aus zwei Teilen. Zuerst wird aus Fischertechnik ein mobiler Roboter gebaut und mit immer feineren Methoden mit der kindgerechten Software RoboPro programmiert. Im Vordergrund steht ein konstruktivistisches und kommunikatives Lernverständnis. Wie können geeignete Lernumgebungen für Jugendliche so geschaffen werden, dass Lernerfolg, Nachhaltigkeit und Spielfreude gewährleistet ist ?

Der zweite Teil besteht in der Durchführung eines zweitägigen Workshops (Freitagnachmittag bis Sonntagmorgen), der im Seminar geplant und von je zwei Teilnehmern in den Semesterferien durchgeführt wird.

Es sind keinerlei Vorkenntnisse erforderlich.____________________________________________________________

Inhalt:
Der Einsatz von Unterrichtsmedien im Mathematikunterricht gewinnt sowohl auf der Ebene der Unterrichtsplanung wie auch der der Unterrichtsrealisierung an Bedeutung. Vor dem Hintergrund konstruktivistischer Lerntheorien zeigt sich, dass der reflektierte Einsatz unter anderem von Computerprogrammen die mathematische Begriffsbildung nachhaltig unterstützen kann. So erlaubt beispielsweise das Experimentieren mit Computerprogrammen mathematische Strukturen zu entdecken, ohne dass dies von einzelnen Routineoperationen (wie z. B. Termumformung) überdeckt würde. Es ergeben sich daraus tiefgreifende Konsequenzen für den Mathematikunterricht. Von daher setzt sich dieses Seminar zum Ziel, den Studierenden die notwendigen Entscheidungs- und Handlungskompetenzen zu vermitteln, um zukünftige Mathematiklehrer auf ihre berufliche Tätigkeit vorzubereiten. Ausgehend von ersten Überlegungen zur Unterrichtsplanung werden anschließend Computer und Tablets hinsichtlich ihres jeweiligen didaktischen Potentials untersucht. Die dabei exemplarisch vorgestellten Systeme sind :

• dynamische Geometrie-Software : Geogebra
• Tabellenkalkulation : Excel
• Apps für Smartphones und Tablet

Jeder Studierende soll Unterrichtssequenz ausarbeiten, die dann in den Übungen besprochen werden.___________________________________________________________________________________________________________

Inhalt:
Geogebra ist eine dynamische Geometriesoftware, die die Möglichkeiten von Computer- algebrasystemen und Dynamischer Geometriesoftware verbindet. Sie wird immer stärker auch im Unterricht eingesetzt.

In diesem Seminar sollen konkrete, unterrichtsrelevante Beispiele aus allen Jahrgangsstufen fachwissenschaftlich und fachdidaktisch aufgearbeitet werden. An ihnen werden Kenntnisse über den Einsatz von Geogebra vermittelt. Dabei wird auch stets der sinnvolle Einsatz von Geogebra thematisiert. Die Erstellung eigener Arbeitsblätter wird angestrebt.

Mögliche Themen sind z. B. der Einsatz von Geogebra im Geometrieunterricht, bei der Behandlung von Extremwert- und Optimierungsaufgaben, bei der Einführung von Ableitung und Integral und im Stochastikunterricht.____________________________________________________________________

Inhalt:
In der praktischen Übung zur Numerik-Vorlesung sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)

R. Plato : Numerische Mathematik kompakt. Vieweg, 2006.

2.)

R. Schaback, H. Wendland : Numerische Mathematik. Springer, 2004.

3.)

J. Stoer, R. Burlisch : Numerische Mathematik I, II. Springer, 2007, 2005.

4.)

G. Hämmerlin, K.-H. Hoffmann : Numerische Mathematik. Springer, 1990.

5.)

P. Deuflhard, A. Hohmann, F. Bornemann : Numerische Mathematik I, II. DeGruyter, 2003.

Inhalt:
 
In den praktischen Übungen sollen die in der Vorlesung „Einführung in die Theorie und Numerik partieller Differentialgleichungen“ vorgestellten numerischen Verfahren zur Lösung partieller Differentialgleichungen implementiert werden. Ziel ist die Erstellung eines Programmpakets zur Berechnung von Näherungslösungen elliptischer Differentialgleichungen mit Hilfe der Finite-Elemente-Methode.

Das Praktikum setzt Programmierkenntnisse in einer Programmiersprache voraus (z. B. C/C++, Matlab, Python, Java, …).

Studierenden, die vorhaben, in der Angewandten Mathematik eine Arbeit zu schreiben, wird die Teilnahme an den praktischen Übungen empfohlen.

Literatur:

1.)

D. Braess, Finite Elemente, Springer, Berlin (2007)

2.)

H. R. Schwarz, Methode der Finiten Elemente, Teubner, Stuttgart (1991)

3.)

G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010)

Inhalt:
In den praktischen Übungen werden die in der Vorlesung „Theorie und Numerik für hyperbolische Erhaltungsgleichungen“ besprochenen Algorithmen implementiert und an praktischen Beispielen getestet. Ziel sind die Implementierung von Finite Differenzen (FD) und Finite Volumen (FV) Verfahren zur numerischen Lösung von skalaren hyperbolischen Erhaltungsgleichungen.

Das Praktikum setzt Kenntnisse in einer gängigen Programmiersprache voraus (z. B. C/C++, Python, Matlab, Java, …).

Studierenden, die das Ziel haben in der Angewandten Mathematik eine Zulassungs- oder Masterarbeit zu schreiben, wird die Teilnahme an den praktischen Übungen empfohlen.___

Inhalt:
Algebraische Geometrie ist ein aktives Gebiet der modernen Mathematik mit Verbindungen zu vielen weiteren Forschungsrichtungen wie der komplexen Geometrie, Differentialgeometrie und Algebra. Es gibt Anwendungen in der Informatik und Cryptographie.

In diesem Proseminar werden die Grundbegriffe der algebraischen Geometrie eingeführt und an konkreten Problemstellungen illustriert.

Literatur:

1.)

Frances Kirwan, Complex Algebraic Curves, Cambridge University Press

2.)

Cox/Little/O’Shea : Ideals, Varieties and Algorithms, Springer

3.)

Hassett, Introduction to Algebraic Geometry, Cambridge University Press

Inhalt:
In diesem Proseminar studieren wir einige grundlegende Themen aus der Graphentheorie. Ein (ungerichteter) Graph ist eine Struktur (V,E) mit einer nicht leeren Menge V von Knoten (vertices) und einer Menge E ⊆{{x,y} : x≠y,x,y ∈ V } von Kanten (edges). Als Beispiel für einen Satz mit einem graphentheoretischen Beweis nennen wir einen Satz von Dilworth über Halbordnungen :

Sei m ≥ 1 eine natürliche Zahl, und sei (H,≤) eine Halbordnung. Wenn in (H,≤) jede Menge von paarweise unvergleichbaren Elementen höchstens m Elemente hat, dann lässt sich H als Vereinigung von höchstens m Ketten schreiben. Eine Kette ist eine Teilmenge, die durch ≤ linear geordnet ist.

Literatur:

1.)

R. Diestel, Graph Theory, 2010

2.)

B. Bollobás, Graph Theory, 1979

Inhalt:
Grob gesagt, beschäftigt sich Kombinatorik mit Abzählen von Elementen in bestimmten endlichen Mengen. Typischerweise handelt es sich dabei um Mengen von Anordnungen (Permutationen), Auswahlen (Kombinationen) und Zerlegungen (Partitionen). Erste einfache Resultate aus der Kombinatorik dürften bereits aus den Anfängervorlesungen und insbesondere Stochastik bekannt sein. Man denke z. B. an den Binomischen Lehrsatz oder Urnenmodelle aus der (elementaren) Stochastik. Im Gegensatz zu vielen anderen Teilgebieten der Mathematik lassen sich typische Probleme der Kombinatorik oft sehr einfach (auch für Nichtmathematiker verständlich) formulieren. Die Lösungen sind mitunter schwerer als es zunächst erscheinen mag. Exemplarisch sei hier das Ménage-Problem erwähnt :

Wir orientieren uns bei der Themenauswahl hauptsächlich an Jacobs & Jungnickel (2003).

Literatur:

1.)

Martin Aigner und und Günter M. Ziegler : Das BUCH der Beweise, Springer 2015 (4. Auflage)

2.)

Titu Andreescu und Zuming Feng : A Path to Combinatorics for Undergraduates, Springer 2004 (ursprünglich Birkhäuser 2004)

3.)

Konrad Jacobs und Dieter Jungnickel : Einführung in die Kombinatorik. De Gruyter 2003 (2. Auflage)

4.)

Peter Tittmann : Einführung in die Kombinatorik. Springer 2014 (2. Auflage)

Inhalt:
Wie groß ist die Wahrscheinlichkeit, dass zwei zufällig gewählte natürliche Zahlen teilerfremd sind ? Überraschenderweise 6∕π², wobei es zunächst völlig unklar erscheinen mag, was Primzahlen überhaupt mit einer Zahl wie π zu tun haben. Wie viele Möglichkeiten gibt es eine natürliche Zahl n als Summe natürlicher Zahlen zu schreiben ? Wenn n klein ist, kann man das von Hand schnell durchprobieren. Für große n wird dies zunehmend unpraktikabel. Man kann jedoch zeigen, dass je größer n, die Zahl ungefähr

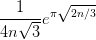
ist. Wir wollen uns mit solchen oder ähnlichen Fragen beschäftigen. Auch damit, was eine algebraische oder transzendente Zahl ist, und warum es kein Polynom mit rationalen Koeffizienten gibt, dass bei π eine Nullstelle hat.

Literatur:

1.)

M. Aigner, G. Ziegler Proofs from THE BOOK (2nd Edition), Springer, 2000

2.)

J. P. Delahaye Pi - Die Story, Birkhäuser, 1999 (Übersetzung des franz. Originals, Le fascinant nombre π, Belin, Pour la Science, 1997)

3.)

D. J. Newman Analytic Number Theory, Springer 1998

4.)

S. Lang Introduction to transcendental numbers, Addison-Wesley 1966

5.)

T. Apostol Introduction to Analytic Number Theory, Springer 1976

Es gibt zahlreiche weitere Quellen, die vergleichbares Material abdecken._____________________________

Inhalt:
Introduced in 1915 by Einstein, General Relativity is a geometric theory of gravitation. It generalizes Special Relativity and Newton’s Law of Gravitation. Its essence are Einstein’s Field Equations, which describe how spacetime is curved by the presence of energy and matter. The goal of this seminar is to derive and discuss Einstein’s Field Equations. Among the topics to be discussed are :

(1)

Newtonian limit and weak gravitation,

(2)

the Schwarzschild solution and predictions for the motions of planets and the bending of light,

(3)

the extended Schwarzschild solution and black holes,

(4)

the Friedmann-Lemaitre-Robertson-Walker solutions and explanation of cosmological redshift and the origins of big-bang.

Inhalt:

Ziel des Seminars ist die Vertiefung des Stoffs der Vorlesung „Elementare Differentialgeometrie“. In den Vorträgen werden weitere Ergebnisse über Kurven und Flächen im euklidischen Raum behandelt werden.

Das Seminar ist vor allem für Studierende des Lehramtsstudiengangs vorgesehen. Frei bleibende Plätze können an Studierende anderer Studiengänge vergeben werden._________________________

Inhalt:
Wir schauen uns Anwendungen der algebraischen Topologie, speziell der Homotopietheorie an. Die genaue Auswahl der Themen erfolgt bei der Vorbesprechung.

Mit den Adams-Operationen in K-Theorie kann man beispielsweise zeigen, dass ℝ, ℂ, ℍ und O die einzigen normierten Divisionsalgebren über ℝ sind. Charakteristische Klassen und Zahlen erlauben eine grobe Bordismus-Klassifikation glatter Mannigfaltigkeiten.

Die Steenrod-Algebra A(p) beschreibt ℤ∕p-Kohomologieoperationen. Für jeden Raum X ist 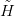^∙(X, ℤ∕p) ein A(p)-Modul, und stetige Abbildungen induzieren A(p)-lineare Abbildungen. Das ermöglicht Aussagen zur Existenz stetiger Abbildungen, beispielsweise lässt sich die maximale Anzahl punktweise linear unabhängiger Vektorfelder auf Sⁿ bestimmen.

Spektralsequenzen sind Folgen von Kettenkomplexen, wobei jeder einzelne Komplex die Homologie seines Vorgängers ist. Erste Beispiele sind die Atiyah-Hirzebruch-Spektralsequenz, mit der man beliebige allgemeine (Ko-) Homologiefunktoren für CW-Komplexe bestimmen kann. Eng verwandt ist die Leray-Serre-Spektralsequenz für Faserbündel.

Mit Hilfe der Adams-Spektralsequenz und A(p) lässt sich die Menge [X,Y ]^s der Homotopieklassen stabiler Abbildungen von X nach Y beschreiben, beispielsweise lassen sich einige stabile Homotopiegruppen der Sphären berechnen.

Für andere Themenvorschläge bin ich offen. Beispielsweise könnten sich im Rahmen der Sommerschule „Mannigfaltigkeiten und K-Theorie“ weitere Themen ergeben.

Literatur:

1.)

J. F. Adams, Stable homotopy and generalised homology, The University of Chicago Press, Chicago, 1974.

2.)

A. Hatcher, Algebraic Topology, Cambridge Univeristy Press, Cambridge, 2002, xii+544S., http://www.math.cornell.edu/~hatcher/AT/ATpage.html

3.)

———, Vector bundles and K-theory, preprint,

http://www.math.cornell.edu/~hatcher/VBKT/VBpage.html

4.)

———, Spectral Sequences in Algebraic Topology, preprint,

http://www.math.cornell.edu/~hatcher/SSAT/SSATpage.html

Inhalt:
Das Seminar behandelt Themen aus der Theorie der zweidimensionalen Minimalflächen, also der Flächen mit mittlerer Krümmung Null. Geometrische Vorkenntnisse sind nicht vorausgesetzt, die notwendigen Begriffe werden mit erarbeitet. Ein Teil der Vorträge basiert auf reellen Methoden wie zum Beispiel dem Maximumprinzip ; ein zweiter Teil wird komplexe Methoden beleuchten, wie sie zum Teil in der Vorlesung über Funktionentheorie im Sommer behandelt wurden. Das Buch von Osserman stellt eine Grundlage für das Seminar dar, die durch weitere Literatur ergänzt wird. Das Seminar wendet sich an Studierende im Bachelor/Master als auch im Lehramt.

Literatur:

1.)

Osserman, R., A survey of minimal surfaces, Van Nostrand 1969.

2.)

Colding, T., Minicozzi, W. P., Minimal Surfaces, New York University 1999.

Inhalt:
Im Seminar lesen wir das neue Buch von Pierre Simon über NIP-Theorien.

Sei T eine vollständige Theorie. Eine Formel ϕ(x,y) hat die Unabhängigbkeitseigenschaft, wenn es für jede Relation R ⊂{1,…n}² ein Modell M von T und Elemente a ₁,…,a_n und b₁,…,b_n in M gibt, sodaß

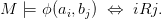
T ist NIP (hat Nicht die Independence Property), wenn keine Formel die Unabhängigkeitseigenschaft hat. Eine Theorie ist genau dann stabil, wenn sie einfach und NIP ist. NIP-Theorien, die nicht einfach sind, sind zum Beispiel o-minimale Theorien, insbesondere die Theorie des Körpers der reellen Zahlen.

Literatur:

1.)

P. Simon A Guide to NIP-Theories, http://www.normalesup.org/~simon/NIP\_guide.pdf oder bei Cambridge University Press

2.)

K. Tent und M. Ziegler A course in Model Theory Lecture Notes in Logic 40, Cambridge UP 2012.

Inhalt:
Dieses Seminar ist ein gemeinsames Seminar mit dem Fraunhofer-Institut für Physikalische Messtechnik IPM in Freiburg. In diesem Seminar werden wir mathematische Modelle für Mehrphasenströmungen mit Phasenübergang herleiten und diese Modelle analysieren und die Lösungen numerisch approximieren. Mehrphasenströmungen entstehen z. B. beim Kochen von Wasser. In diesem Falle sind die beiden Phasen Wasser bzw. Wasserdampf. Ständig wird Wasser verdampft bzw. Wasserdampf kondensiert.
Ein anderes Beispiel kommt vor im Zusammenhang mit der magnetokalorischen Kühlung. In diesem Falle werden zur Erwärmung des Wassers Materialien verwendet, die durch Anlegen eines Magnetfeldes ihre Temperatur ändern. Durch geschickte Anordnung dieser Magneten und geeignete Änderung des Magnetfelds kann man in periodischer Weise Wasser zum Verdampfen bzw. Kondensieren bringen und damit einen Kühlprozess initiieren. Das technologische Fernziel dieses Prozesses ist die Ersetzung von Fluorkohlenwasserstoffen als Kühlmittel durch diesen magnetokalorischen Prozess.

Das Seminar richtet sich an Studierende ab dem 5. Semester, die Erfahrungen haben im Bereich partielle Differentialgleichungen und Numerik._________________________________________________________

Inhalt:
Im Seminar sollen grundlegende Eigenschaften von Sobolev-Funktionen sowie deren Approximation durch Finite-Elemente Funktionen diskutiert werden. Ein wesentlicher Aspekt ist dabei die Vermeidung von höheren Regularitätsannahmen.

Literatur:

1.)

M. Dobrowolski : Angewandte Funktionalanalysis, Springer, 2010.

2.)

H.-W. Alt : Lineare Funktionalanalysis, Springer, 2002.

3.)

S.C. Brenner, L.R. Scott : The Mathematical Theory of Finite Element Methods, Springer, 2007.

4.)

R.A. Adams, J.J.F. Fourner : Sobolev Spaces, Academic Press, 2003.

5.)

W.P. Ziemer : Weakly Differentiable Functions, Springer, 1989.

Inhalt:
 
Wir beginnen mit dem allgemeinen Formalismus der Kategorientheorie nach [Saunders-MacLane]. Im weiteren Verlauf studieren wir dann monoidale Kategorien und ihre Beziehung zu Quantengruppen nach [Kassel].

Literatur:

1.)

Saunders-MacLane, Categories for the working mathematician

2.)

Christian Kassel, Quantum groups

Inhalt:

Das Seminar behandelt Fragestellungen betreffend den Zusammenhang zwischen den topologischen Eigenschaften eines Raumes X und den algebraischen Eigenschaften des Ringes C(X) der stetigen reellwertigen Funktionen auf X, bzw. des Teilringes C^*(X) der beschränkten Funktionen in C(X). Insbesondere wird die Frage der Charakterisierbarkeit eines Raumes X durch die Ringe C(X) bzw. C^*(X) untersucht. Hierbei kommt den Nullstellenmengen stetiger Funktionen besondere Bedeutung zu.

Literatur:

1.)

[GJ] Gillman and Jerison, Rings of Continuous functions

Vor der Vorbesprechung sollten Sie sich [GJ] 0.8 bis 0.11 kurz ansehen.
(Hierbei können Sie vorläufig annehmen, dass alle vorkommenden Räume metrisch sind. Ein Raum ist kompakt, sofern jede Überdeckung des Raumes durch offene Mengen eine endliche Teilüberdeckung besitzt.)
______________________________________________________________________________________________________________________________

Inhalt:

Der Zusammenhang zwischen den topologischen Eigenschaften eines Raumes X und den algebraischen Eigenschaften des Ringes C(X) der stetigen reellwertigen Funktionen auf X wird zur Untersuchung verschiedener mathematischer Objekte wie der Stone-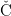ech-Kompaktifizierung, der hyper-reellen Zahlen, des Dimensionsbegriffes oder nichtmessbarer Kardinalzahlen angewandt.

Literatur:

1.)

[GJ] Gillman and Jerison, Rings of Continuous functions

Das Seminar kann auch gemeinsam mit dem Seminar ’Ringe stetiger Funktionen : Grundlagen’ besucht werden.
______________________________________________________________________________________________________________________________

Inhalt:
Moderne statistische Methoden und Modellierungstechniken im Bereich der Biostatistik adressieren komplexe Fragestellungen in den biomedizinischen Wissenschaften, wie z.B. die Einbeziehung molekularer Information in Studien zur Ätiologie, Diagnose/Prognose und Therapie. Eine Auswahl solcher Problemstellungen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren ; die genaue thematische Ausrichtung wird noch festgelegt.

Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als Einführung in die Thematik dienen.

Das Hauptseminar ist terminlich und inhaltlich mit dem Oberseminar „Medizinische Statistik“ abgestimmt.

Literatur wird in der Vorbesprechung bekannt gegeben.

Das Seminar beginnt am 21.10.2015 und endet mit dem 10.02.2016._____________________________