[prev] [prev-tail] [tail] [up]

Lehrveranstaltungen

 

1. Vorlesungen

PIC

WS2014/15 PIC________________________________________________________

Vorlesung:  

Stochastik (1. Teil der zweisemestrigen Veranstaltung)

  

Dozent:  

Prof. Dr. L. Rüschendorf

  

Zeit/Ort:  

Di 16–18 Uhr, HS Rundbau, Albertstr. 21

  

Übungen:  

2-stündig (14-täglich) n.V.

  

Tutorium:  

B. Köpfer

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/Vorlesungen

  
 
_______________________________________________________________

Inhalt:
 
Die Vorlesung führt in die stochastische Modellbildung ein und erläutert Begriffe und Resultate der Wahrscheinlichkeitstheorie. Grundlegend sind hierbei diskrete und stetige Wahrscheinlichkeitsverteilungen sowie Zufallsvariablen. Wichtige Resultate umfassen etwa das Gesetz der großen Zahlen und den zentralen Grenzwertsatz.

Die Vorlesung wird im SS 2015 durch eine weitere 2-stündige Vorlesung fortgesetzt, dann wird es auch Praktischen Übungen zur Stochastik geben.

Der Stoff der Vorlesung kann als Prüfungsstoff für Staatsexamensprüfungen herangezogen werden.

Literatur:

1.)
Krengel, U.: Einführung in die Wahrscheinlichkeitstheorie und Statistik. Vieweg, 1988
2.)
Georgii, H. O.: Stochastik: Einführung in die Wahrscheinlichkeitstheorie und Statistik. de Gruyter, 2002
_______________________________________________________________________________________________________

Typisches Semester:  

ab 3. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis I

Prüfungsleistung:  

Klausur

Folgeveranstaltungen:  

Stochastik (2. Teil der Vorlesung); Praktische Übungen zur Stochastik

Sprechstunde Dozent:  

Mi, 11–12 Uhr, Zi. 242, Eckerstr. 1

Sprechstunde Assistent:  

Mi, 10–11 Uhr, Zi. 227, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Numerik (1. Teil der zweisemestrigen Veranstaltung)

  

Dozent:  

Prof. Dr. D. Kröner

  

Zeit/Ort:  

Mi 12–14 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-stündig (14-täglich) n.V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
In dieser Vorlesung werden die Grundlagen für numerische Algorithmen die in der angewandten Mathematik zur Anwendung kommen, gelegt. Themen dieser Vorlesung sind: Zahlendarstellung auf Rechnern, Matrixnormen, Banachscher Fixpunktsatz, lineare und nichtlineare Gleichungssysteme, Berechnung von Eigenwerten und Grundlagen der linearen Optimierung.
Parallel zur Vorlesung wird eine praktische Übung angeboten, in dem die in der Vorlesung besprochenen Algorithmen auf Computern implementiert und an verschiedenen Beispielen getestet werden.
Die praktische Übung findet 14-täglich im Wechsel mit der Übung zur Vorlesung statt. Diese Vorlesung wird als zweisemestrige Vorlesung im SS 2015 fortgesetzt.

Literatur:

1.)
J. Stoer, R. Bulirsch: Numerische Mathematik I, II. Springer 2007, 2005.
2.)
P. Deuflhard, A. Hohmann/F. Bornemann: Numerische Mathematik I, II. De Gruyter 2003, 2002.
3.)
G. Hämmerlin, K. H. Hoffmann: Numerische Mathematik. Springer 1990.
________________________

Typisches Semester:  

3. Semester

ECTS-Punkte:  

für beide Teile zusammen 9 Punkte

Notwendige Vorkenntnisse:  

Grundvorlesungen in Linearer Algebra und Analysis

Sprechstunde Dozent:  

Mi 11–12 Uhr, Raum 215, Hermann–Herder-Str. 10

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Algebra und Zahlentheorie

  

Dozent:  

Markus Junker

  

Zeit/Ort:  

Mo, Mi 14–16 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

B. Taji

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/junker/ws14/algebra.html

  
 
_______________________________________________________________

Inhalt:
Die Vorlesung wird in die Theorie der Gruppen, Ringe und Körper einführen. Ziel der Vorlesung ist vor allem die Galois-Theorie der algebraischen Körpererweiterungen, mit der sich u. a. zeigen lässt, dass es, anders als für quadratische Gleichungen, für Polynomgleichungen ab Grad 5 keine Lösungsformel mehr gibt.

Weitere Stichworte zum Inhalt und weitere Literaturangaben finden sich im Modulhandbuch.

Die Vorlesung ist eine Pflichtveranstaltung im Lehramtsstudium nach GymPO und eine geeignete weiterführende Vorlesung für das Bachelor-Studium. Sie zählt zur Reinen Mathematik und gehört zur Kategorie II, d. h. sie kann im Master-Studiengang nur eingeschränkt verwendet werden.

In jedem Fall wird die erfolgreiche Teilnahme an der Abschlussklausur gefordert; entweder als Prüfungsleistung (im Bachelor- und im Lehramtsstudiengang nach GymPO) oder als zusätzliche Studienleistungen zu den Übungen (im Master-Studiengang und ggf. für Studierende anderer Fächer).

Literatur:

1.)
S. Lang, „Algebra“, Springer.
2.)
M. Junker, Skript zur Algebra-Vorlesung, WS 2007/08.
3.)
F. Lorenz, „Einführung in die Algebra“, BI.
_______________________________________________________________

Typisches Semester:  

ab 3. Fachsemester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Lineare Algebra I und II

Studienleistung:  

Bearbeiten der Übungsaufgaben; ggf. Abschlussklausur

Prüfungsleistung:  

Abschlussklausur

Sprechstunde Dozent:  

Di 14–15 Uhr, Zi. 423, Eckerstr. 1

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Mehrfachintegrale

  

Dozent:  

Prof. Dr. W. Soergel

  

Zeit/Ort:  

Mi 9–12 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Beginn:  

Mi, 7.1.2015

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

D. Hein

  
 
_______________________________________________________________

Inhalt:
Das mehrdimensionale Riemann-Integral ist eine direkte Verallgemeinerung des Riemann-Integrals aus der Analysis-Vorlesung. Es erlaubt, stetige Funktionen über geeignete „einfache“ kompakte Gebiete im ℝn zu integrieren. Wir beweisen in diesem Kontext den Satz von Fubini und die Transformationsformel, mit deren Hilfe sich diese Integrale oft auf mehrere eindimensionale Integrale zurückführen lassen Außerdem führen wir Oberflächenintegrale ein. Wenn die Zeit reicht, lernen wir elementare Formen der Integralsätze von Stokes und Gauß kennen.

Literatur:

1.)
W. Walter, Analysis 2, 5. erw. Aufl., Springer, Berlin, 2002
___________________________________________

Typisches Semester:  

5. Semester (nach Ende des Praxissemesters)

ECTS-Punkte:  

2 Punkte

Notwendige Vorkenntnisse:  

Analysis I, II, Lineare Algebra I

Studienleistung:  

Regelmäßige Teilnahme an den Übungen, evtl. Klausur

Sprechstunde Dozent:  

Do 11:30–12:30 Uhr, Zi. 429, Eckerstr. 1

Kommentar:  

Diese Veranstaltung richtet sich ausschließlich an Studierende des Lehramts

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Analysis III

  

Dozent:  

Prof. Dr. V. Bangert

  

Zeit/Ort:  

Di, Do 10–12 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-stündig n. V.

  

Tutorium:  

H. Eberlein

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/geometrie/lehre/ws2014/vorlesung/AnalysisIII/

  
 
_______________________________________________________________

Inhalt:

Der Inhalt der Vorlesung ist Voraussetzung für weite Teile der Analysis, der Geomerie und der Stochastik. Die Vorlesung beginnt mit einer Einführung in die Maß- und Integrationstheorie, die allgemein genug ist, um als Grundlage für die Wahrscheinlichkeitstheorie zu dienen. Das bedingt einen höheren Abstraktionsgrad als für die Integration im ℝn notwendig, führt aber andererseits zu sehr klaren Begriffsbildungen. Als Spezialfall wird das Lebesguemaß konstruiert. Die Methoden zur Berechnung von Integralen von Funktionen mehrerer Veränderlicher (Satz von Fubini, Transformationssatz) werden hergeleitet. Auf der Grundlage des Transformationssatzes wird das Flächenmaß von Untermannigfaltigkeiten des ℝn eingeführt. Schließlich wird als Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung der Gaußsche Integralsatz bewiesen. Die Vorlesung stützt sich auf das Skriptum von Prof. Růžička aus dem WS 2009/10.

Literatur:

1.)
J. Elstrodt: Maß- und Integrationstheorie, (5. Aufl.) Springer 2007.
2.)
H. Amann, J. Escher: Analysis III, Birkhäuser 2001.
__________________________________________________

Typisches Semester:  

ab 3. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis I, II, Lineare Algebra I

Studienleistung:  

Regelmäßige und aktive Teilnahme an den Übungen, 50% der Übungsaufgaben

Sprechstunde Dozent:  

Di 14–15 Uhr, Zi. 335, Eckerstr. 1

Sprechstunde Assistent:  

Do 14–15 Uhr, Zi. 144, Eckerstr. 1

 

PIC

WS2014/15 PIC_________________________________________________________

Vorlesung:  

Wahrscheinlichkeitstheorie

  

Dozent:  

Prof. Dr. H. R. Lerche

  

Zeit/Ort:  

Di, Do 12–14 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/Vorlesungen

  
 
_______________________________________________________________

Inhalt:
 
Die Wahrscheinlichkeitsheorie beschreibt mathematisch zufällige Vorgänge. Legt man die Axiomatisierung von Kolmogorov zugrunde, so ist sie eine mathematische Theorie, deren Formulierung mit Hilfe der Maßtheorie geschieht. Die Vorlesung gibt eine systematische Einführung in diese Theorie. Sie ist grundlegend für alle weiterführenden Lehrveranstaltungen aus dem Bereich der Stochastik.

Vor allem werden die klassischen Grenzwertsätze behandelt, wie Kolmogorovs 0-1 Gesetz, das Gesetz der großen Zahlen und der zentrale Grenzwertsatz. Neben bedingten Erwartungen sollen auch Martingale behandelt werden.

Literatur:

1.)
Georgii, H.-O.: Stochastik, Walter de Gruyter, 2007
2.)
Klenke, A.: Wahrscheinlichkeitstheorie, Springer, 2006
3.)
Shiryaev, A.: Probability, 2. Auflage, Springer 1996
4.)
Williams, D.: Probability with Martingales, Cambridge University Press, 1991
__________________

Typisches Semester:  

ab 5. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis I u. II, Lineare Algebra I u. II

Prüfungsleistung:  

Klausur

Sprechstunde Dozent:  

Di, 11–12 Uhr, Zi. 233, Eckerstr. 1

 
PIC      
Abteilung für
Mathematische Logik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Modelltheorie

  

Dozentin:  

Heike Mildenberger

  

Zeit/Ort:  

Mo, Mi 10–12 Uhr, SR 404, Eckerstr. 1

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/mildenberger/veranstaltungen/ws14/modelltheorie.html

  
 
_______________________________________________________________

Inhalt:
In der Modelltheorie untersucht man Zusammenhänge zwischen formalen Sprachen und ihren Interpretationen, den Modellen. Wir setzen die Kenntnis des Vollständigkeitssatzes voraus. Wir studieren Morleys Satz von 1962, dass jede erststufige Theorie, die in einer Mächtigkeit oberhalb der Anzahl der Symbole bis auf Isomorphie genau ein Modell hat, im Wesentlichen einen Vektorraum axiomatisiert. Danach befassen wir uns mit der sogenannten Stabilitätstheorie, die ihren Namen durch Shelahs Einteilung der Theorien in stabile und unstabile erhielt und seitdem auch für gewisse unstabile Theorien und allgemeinere, nicht erststufig gegebene Modellklassen weiterentwickelt wird. Wir widmen uns den von Hrushovski konstruierten Fra¨issé-Limiten, die zeigen, dass es nicht nur bei algebraisch abgeschlossenen Körpern Prägeometrien und streng minimale Mengen gibt.

Literatur:

1.)
Chang, C. C. and Keisler, H. J., Model theory, Third Ed., North–Holland Publishing Co., Amsterdam, 1990,
2.)
Hodges, Wilfrid, Model theory, Cambridge University Press, Cambridge, 1993,
3.)
Tent, Katrin und Ziegler, Martin, A course in model theory, Association for Symbolic Logic, La Jolla, CA, 2012
________________________________________________________________________________________________

Typisches Semester:  

mittleres

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Mathematische Logik

Folgeveranstaltungen:  

Modelltheorie II

Studienleistung:  

Teilnahme an den Übungen

Prüfungsleistung:  

mündliche Prüfung

Sprechstunde Dozentin:  

Di 13–14 Uhr, Raum 310, Eckerstr. 1

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Algebraische Topologie

  

Dozent:  

Prof. Dr. Sebastian Goette

  

Zeit/Ort:  

Di, Do 10–12 Uhr, Hörsaal II, Albertstr. 23b

  

Übungen:  

Mo 10–12, Mo 14–16 oder Mi 10–12 Uhr, SR 119, Eckerstr. 1

  

Tutorium:  

Dr. Doris Hein

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/goette/

  
 
_______________________________________________________________

Inhalt:
Die algebraische Topologie untersucht topologische Räume mit algebraischen Methoden. Sie wird in vielen Bereichen der Mathematik von der Differentialgeometrie über die komplexe und algebraische Geometrie bis hin zur Gruppentheorie verwendet.

In der Vorlesung betrachten wir als erstes höhere Homotopiegruppen als Verallgemeinerung der Fundamentalgruppe. Als Anwendung erhalten wir einige klassische Sätze, zum Beispiel den Brouwerschen Fixpunktsatz. Homotopiegruppen sind zwar sehr mächtige Invarianten, in der Praxis aber nicht einfach zu bestimmen.

Homologie- und Kohomologiegruppen sind mit Homotopiegruppen entfernt verwandt, lassen sich aber besser axiomatisch charakterisieren und leichter berechnen. Sie tragen zusätzliche Strukturen, zum Beispiel das Cup-Produkt auf der Kohomologie. Wir wollen diese Invarianten in einer Sprache beschreiben, die sich später auch für andere topologische Konstruktionen wie K-Theorie, stabile Homotopie und Kobordismus benutzen lässt.

Bei Interesse wird die Vorlesung im SS 2015 als Spezialvorlesung und/oder Lesekurs fortgesetzt. Wir werden dann unter anderem Poincaré-Dualität für topologische Mannigfaltigkeiten kennenlernen.

Literatur:

1.)
T. tom Dieck: Algebraic Topology, EMS Textbooks in Mathematics, EMS, Zürich, 2008.
2.)
A. Hatcher: Algebraic Topology, Cambridge University Press, 2002, http://www.math.cornell.edu/~hatcher/AT/ATpage.html
__________________________

Typisches Semester:  

5. Semester B.Sc., 1. Semester Master

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Topologie

Folgeveranstaltungen:  

Algebraische Topologie II, s.o.

Sprechstunde Dozent:  

Mi 13:10–13:55 Uhr, Raum 340, Eckerstr. 1

Sprechstunde Assistentin:  

n. V., Raum 323, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung::  

Einführung in die Theorie und Numerik partieller Differentialgleichungen

  

Dozent:  

Prof. Dr. D. Kröner

  

Zeit/Ort:  

Mo, Mi 10–12 Uhr, HS II, Albertstr. 23 b

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
Partielle Differentialgleichungen sind Gleichungen, die einen Zusammenhang zwischen einer Funktion u, deren partiellen Ableitungen und weiteren gegebenen Funktionen beinhalten, z. B.

- ∂xxu (x,y) - ∂yyu(x,y) = f (x,y) fu¨r (x,y ) ∈ Ω,
wobei Ω eine Teilmenge des ℝ2 ist. Diese Differentialgleichung ist vom elliptischen Typ und steht im Mittelpunkt der Vorlesung. Das zu lösende Problem besteht nun darin, zu gegebenen Funktionen f : Ω → ℝ2 und g : ∂Ω → ℝ2 eine Funktion u : Ω → ℝ2 zu finden, welche die obige Differentialgleichung löst und die Randbedingung
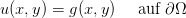
u(x,y) = g (x, y) auf ∂ Ω
erfüllt.
Partielle Differentialgleichungen treten oft als Modelle für physikalische Vorgänge auf. Das obige Beispiel beschreibt z. B. die Temperaturverteilung u in einem Raum Ω, wenn der Raum gemäß der Funktion f aufgeheizt wird und die Wände (∂Ω) des Raumes auf der Temperatur g gehalten werden.
Da sich eine explizite Lösung nur in Spezialfällen finden lässt, muss man sich zunächst auf die Untersuchung der Frage, ob es überhaupt Lösungen gibt und wenn ja, wie viele, beschränken. Der nächste Schritt, der den Schwerpunkt der Vorlesung bildet, ist die numerische Berechnung von Näherungslösungen mit Hilfe der Finite-Elemente-Methode. Neben der Darstellung des Verfahrens steht die Herleitung von Fehlerabschätzungen im Vordergrund. Parallel zu der Vorlesung werden eine Übung und eine praktische Übung (siehe Kommentar zur praktischen Übung) angeboten.

Literatur:

1.)
D. Braess, Finite Elemente, Springer, Berlin (2007).
2.)
G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010).
______

Typisches Semester:  

5. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis und Lineare Algebra

Sprechstunde Dozent:  

Mi 11–12 Uhr, Raum 215, Hermann–Herder–Str. 10

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Geometrische Analysis

  

Dozent:  

Prof. Dr. Wang

  

Zeit/Ort:  

Mo, Mi 12–14 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

Dipl.-Math. M. Mattuschka

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/wang

  
 
_______________________________________________________________

Inhalt:

Die Vorlesung bietet eine Einführung in die Geometrische Analysis, zu Beginn des Master-Studiengangs sowie für fortgeschrittene Studierende im Bachelor. Es werden analytische Techniken im Kontext von geometrischen Fragestellungen behandelt, etwa:

L2-Regularitätstheorie für elliptische Systeme auf Mannigfaltigkeiten und Anwendung auf harmonische Differentialformen, C2,α-Regularitätstheorie für parabolische Systeme auf Mannigfaltigkeiten und Anwendung auf die Kurzzeitexistenz für geometrische Evolutionsgleichungen, zum Beispiel den mittleren Krümmungsfluss, Einbettungssätze von Sobolev mit Anwendungen auf konform invariante Variationsprobleme.

Die benötigten Hilfsmittel aus der Differentialgeometrie werden mit entwickelt.

Literatur:

1.)
Aubin, T., Nonlinear Analysis on Manifolds. Monge-Ampère Equations, Springer, 1982.
2.)
Jost, J., Riemannian Geometry and Geometric Analysis, Springer, 2008.
________________________

Typisches Semester:  

ab dem 5. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Funktionalanalysis

Folgeveranstaltungen:  

Seminar Geometrische Analysis

Studienleistung:  

Übungsaufgaben

Prüfungsleistung:  

mündliche Prüfung

Sprechstunde Dozent:  

Mi 10:30-11:30 Uhr, Raum 210, Eckerstr. 1

Sprechstunde Assistent:  

Mo, Mi 10–12 Uhr, Raum 203 Eckerstr. 1

 
PIC
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Stochastische Prozesse

  

Dozent:  

Prof. Dr. Peter Pfaffelhuber

  

Zeit/Ort:  

Di, Fr 14–16 Uhr, HS Weismann-Haus, Albertstr. 21 a

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

Felix Hermann

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
Die Vorlesung ist die erste Veranstaltung im Studiengang Master of Science Mathematik, Studienschwerpunkt Wahrscheinlichkeitstheorie, Finanzmathematik und Statistik, insbesondere in der neuen Profillinie Finanzmathematik. Sie schließt direkt an die Vorlesung Wahrscheinlichkeitstheorie aus dem WS 2013/14 an.

Ein stochastischer Prozess (Xt)t∈I ist nichts weiter als eine Familie von Zufallsvariablen, wobei etwa I = [0; ∞) eine kontinuierliche Zeitmenge ist. Einfache Beispiele sind Irrfahrten, Markov-Ketten, die Brown’sche Bewegung oder davon abgeleitete Prozesse. Letztere spielen vor allem in der Modellierung von finanzmathematischen oder naturwissenschaftlichen Fragestellungen eine große Rolle.

Wir werden uns zunächst mit der reichhaltigen Klasse von Martingalen beschäftigen und die wichtigen Martingalkonvergenzsätze kennen lernen. Anschließend konstruieren wir die Brown’sche Bewegung und studieren ihre Pfadeigenschaften. Infinitesimale Charakteristiken eines Marko-Prozesses werden durch Generatoren beschrieben, was eine Verbindung zur Theorie von partiellen Differentialgleichungen ermöglicht. Abschließend kommt mit dem Ergodensatz für stationäre stochastische Prozesse eine Verallgemeinerung des Gesetzes der großen Zahlen zur Sprache.

Im Sommersemester 2015 wird diese Veranstaltung durch die Vorlesung Stochastische Integration und Finanzmathematik fortgeführt.

Literatur:

1.)
O. Kallenberg. Foundation Bitte Wochentag, Uhrzeit, Raum und Strasse angeben s of Modern Probability (Probability and Its Applications). Springer 2002
2.)
A. Klenke. Wahrscheinlichkeitstheorie. Springer 2006
3.)
D. Williams. Probability with Martingales (Cambridge Mathematical Textbooks). Cambridge University Press 1991
_________________________________________________________________________________________________________________________

Typisches Semester:  

1. Semester Master

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Wahrscheinlichkeitstheorie

Folgeveranstaltungen:  

Stochastische Integration und Finanzmathematik

Sprechstunde Dozent:  

Fr 16–17 Uhr, Zi. 241, Eckerstr. 1

Sprechstunde Assistent:  

wird noch mitgeteilt

 
PIC    
Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Theorie und Numerik partieller Differentialgleichungen I

  

Dozent:  

Prof. Dr. S. Bartels

  

Zeit/Ort:  

Di, Do 10–12 Uhr, SR 226, Hermann-Herder-Str. 10

  

Übungen:  

Do 14–16 Uhr, SR 226, Hermann-Herder-Str. 10

  

Tutorium:  

Marijo Milicevic, MSc

  

Web-Seite:  

http://aam.uni-freiburg.de/bartels

  
 
_______________________________________________________________

Inhalt:
Die numerischen Methoden zur Behandlung elliptischer partieller Differentialgleichungen führen zu Schwierigkeiten, wenn das Problem kleine Parameter enthält oder Nebenbedingungen erfüllt werden müssen. Diese Aspekte treten beispielsweise bei der mathematischen Beschreibung von Festkörpern und Fluiden auf. In der Vorlesung sollen die theoretischen Eigenschaften solcher Modelle analysiert und geeignete numerische Verfahren entwickelt werden.

Literatur:

1.)
D. Braess: Finite Elemente. Springer, 2007.
2.)
D. Boffi, F. Brezzi, M. Fortin: Mixed Finite Element Methods and Applications. Springer, 2013.
3.)
M. Dobrowolski: Angewandte Funktionalanalysis. Springer, 2005.
4.)
P. Knabner, L. Angermann: Numerical Methods for Elliptic and Parabolic PDEs. Springer, 2000.
5.)
C. Grossmann, H.-G. Roos: Numerische Behandlung partieller Differentialgleichungen. Springer, 2005.
_____________________________________________________________________________________________________

Typisches Semester:  

7. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Einführung in Theorie und Numerik partieller Differentialgleichungen

Studienleistung:  

Aktive Teilnahme an den Übungen

Prüfungsleistung:  

Mündliche Prüfung

Sprechstunde Dozent:  

Mi 12–13 Uhr und n.V., Zimmer 209, Hermann-Herder-Str. 10

Sprechstunde Assistent:  

Wird in der Vorlesung bekannt gegeben

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Introduction to Harish–Chandra modules

  

Dozent:  

Pavle Pandžić (voraussichtlich)

  

Zeit/Ort:  

Di, Do 14–16 Uhr, HS II, Albertstr. 23b

  

Tutorium:  

N. N.

  
 
_______________________________________________________________

Inhalt:
We will study infinite-dimensional representations of Lie groups, mostly through their algebraic versions, Harish-Chandra modules. Special attention will be given to the construction of Harish-Chandra modules by the so called cohomological induction, which involves derived functors. Properties of cohomologically induced modules, like irreducibility and unitarity, will be proved in detail.

Literatur:

1.)
Knapp and Vogan: Cohomological induction and unitary representations, Princeton University Press, 1995
2.)
Huang and Pandžić: Dirac operators in representation theory, Birkhäuser, 2006
3.)
Pandžić: Lectures on cohomological induction (informal notes that will be distributed in class)
_________________________________________________________________________________________________________________

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Basic linear algebra (as in standard undergraduate courses), Basic abstract algebra (groups, rings and modules)

Nützliche Vorkenntnisse:  

Basic theory of Lie groups and/or Lie algebras, Representations of compact groups, Homological algebra (derived functors)

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Monstrous Moonshine

  

Dozentin:  

K. Wendland

  

Zeit/Ort:  

Mo, Mi 10–12 Uhr, SR 226, Hermann-Herder-Str. 10

  

Übungen:  

2-stündig n. V.

  

Tutorium:  

Dr. E. Scheidegger

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/mathphys/lehre/WiSe14/Monster.html

  
 
_______________________________________________________________

Inhalt:
Die Moonshine-Vermutung stellt einen unerwarteten Zusammenhang her zwischen der größten sporadischen Gruppe, der sogenannten Monster-Gruppe, sowie einer wichtigen, auf der oberen Halbebene holomorphen Funktion, der Modulfunktion j.

In der Klassifikation der endlichen einfachen Gruppen treten 26 Ausnahmegruppen in Erscheinung, die „sporadische“ Gruppen. Die Monster-Gruppe M ist die größte unter diesen. Sie besitzt

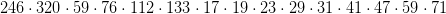
246 ⋅ 320 ⋅ 59 ⋅ 76 ⋅ 112 ⋅ 133 ⋅ 17 ⋅ 19 ⋅ 23 ⋅ 29 ⋅ 31 ⋅ 41 ⋅ 47 ⋅ 59 ⋅ 71
Elemente. Eine Modulfunktion ist eine meromorphe Funktion auf der oberen komplexen Halbebene, die unter Möbiustransformationen invariant ist. Für die einfachste unter diesen, die j-Funktion, beginnt die Fourierreihe wie folgt:
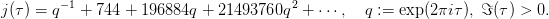
j(τ) = q- 1 + 744 + 196884q + 21493760q2 + ⋅⋅⋅, q := exp(2πiτ), ℑ(τ ) > 0.
Sehr merkwürdig: Die Koeffizienten 196884, 21493760,… sind in sehr einfacher Weise mit den Dimensionen der irreduziblen Darstellungen von M verknüpft. Die „Monstrous-Moonshine“-Vermutung besagt, dass es hierfür einen tieferen Grund gibt – und natürlich sehr viel mehr als das. Genauso mysteriös wie die Vermutung selbst ist deren schließlich von Borcherds gefundener Beweis: Diesen kann man am besten verstehen, wenn man in eine physikalisch motivierte Theorie hineinschaut – die konforme Quantenfeldtheorie.

Ziel der Vorlesung ist es, Aussage sowie Grundzüge des Beweises der „Monstrous-Moonshine“-Vermutung zu erarbeiten. Dazu werden die wesentlichen Grundbegriffe und Ergebnisse aus der Theorie der endlichen Gruppen, der Modulformen sowie aus der konformen Feldtheorie eingeführt. Hierbei spielt eine unendlich-dimensionale Liealgebra, die sogenannte Virasoro-Algebra, eine zentrale Rolle. Weiter werden die grundlegenden Konstruktionen von Vertexoperator-Algebren diskutiert. Einige Vorlesungsstunden werden den Zusammenhängen mit den Quantenfeldtheorien gewidmet, Vorkenntnisse aus der Physik werden aber nicht vorausgesetzt.

Anmerkung: Möglicherweise muss ein Teil der Vorlesung als „Reading-Course“ durchgeführt werden; Einzelheiten hierzu werden in der ersten Vorlesung bekannt gegeben.

  Fortsetzung auf der nächsten Seite

Fortsetzung des Kommentars zu “Monstrous Moonshine”, Prof. Wendland

Literatur:

1.)
T. Gannon, Moonshine Beyond the Monster, Cambridge University Press, 2006
2.)
R. Borcherds Proceedings of the I.C.M., Vol. I (Berlin, 1998). Doc. Math. 1998, Extra Vol. I, 607–615, http://math.berkeley.edu/~reb/papers/icm98/icm98.pdf
____________________________________________________________________________________

Typisches Semester:  

ab 6. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Funktionentheorie, Differentialgeometrie, elementare Vorkenntnisse zu Liealgebren

Nützliche Vorkenntnisse:  

komplexe Geometrie, Modulformen

Sprechstunde Dozentin:  

Mi 13–14 Uhr, Rm 337/338, Eckerstr. 1

Sprechstunde Assistent:  

Mi 16–17 Uhr, Rm 329, Eckerstr. 1

 
PIC
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Mathematische Statistik

  

Dozent:  

Prof. Dr. Ludger Rüschendorf

  

Zeit/Ort:  

Mo, Mi 14–16 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

J. Ansari

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
 
Die Vorlesung „Mathematische Statistik“ baut auf Grundkenntnissen aus der Wahrscheinlichkeitstheorie auf. Das grundlegende Problem der Statistik ist die begründete Anpassung eines statistischen Modells zur Beschreibung eines Experimentes. Hierzu wird in der Vorlesung in die wichtigsten Methoden aus der statistischen Entscheidungstheorie wie Test- und Schätzverfahren eingeführt. Weitere Themen sind Ordnungsprinzipien zur Reduktion der Komplexität der Modelle (Suffizienz und Invarianz) sowie einführende Betrachtungen zur asymptotischen Statistik.

Literatur:

1.)
Rüschendorf, L.: Mathematische Statistik, Springer 2014
_______________________________________________

Typisches Semester:  

ab 7. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Wahrscheinlichkeitstheorie

Sprechstunde Dozent:  

Di 11–12 Uhr, Zi. 242, Eckerstr. 1

Sprechstunde Assistent:  

wird noch mitgeteilt

 

Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Metric measure spaces with lower Ricci curvature bounds

  

Dozent:  

Christian Ketterer

  

Zeit/Ort:  

Di 10–12 Uhr, SR 127, Eckerstr. 1

  
 
_______________________________________________________________

Inhalt:

The course gives an introduction to metric measure spaces with generalized lower Ricci curvature bounds in the sense of Lott, Sturm and Villani. We will provide concepts on metric measure spaces and optimal transport that will be needed in the course. Then the definition of generalized lower Ricci curvature bounds and the coherence with the classical approach for smooth Riemannian manifolds will be presented.

The topics will be:

1.
Metric (measure) spaces (definitions, Gromov–Hausdorff distance, Alexandrov spaces, . . .) [1]
2.
Optimal transport (couplings, Monge–Kantorovich problem, Kantorovich duality, . . .) [2], [3]
3.
Optimal transport in metric measure spaces (Wasserstein space, displacement convexity, . . .) [2], [3]
4.
Generalized Ricci curvature bounds – (definition, consequences, coherence, . . .) [2], [3]

Literatur:

[1]
Burago, Burago, Ivanov, A course in metric geometry, Book
[2]
C. Villani, Optimal transport (old and new), Book
[3]
K.-T. Sturm, On the geometry of metric measure spaces I + II, Acta Math., 196 (2006)
_____

Typisches Semester:  

5. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Analysis 1, 2 & 3

Sprechstunde Dozent:  

wird in der Vorlesung mitgeteilt

 
PIC
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Verzweigungsprozesse und Anwendungen

  

Dozent:  

Dr. Andrej Depperschmidt

  

Zeit/Ort:  

Do 10–12 Uhr, SR 127, Eckerstr. 1

  

Übungen:  

2-stündig n.V.

  

Tutorium:  

Maximilian Gerhards

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
In dieser Vorlesung wird es um Verzweigungsprozesse und deren Anwendungen in Perkolationstheorie und Theorie der zufälligen Graphen gehen. Auch Anwendungen in Biologie werden besprochen.

Wir beginnen mit Bienaymé-Galton-Watson-Prozessen (das sind Verzweigungsprozesse in diskreter Zeit) und ihren Eigenschaften. Danach behandeln wir verschiedene Erweiterungen wie z.B. Verzweigungsprozesse mit Immigration und altersabhängiger Verzweigung. Je nach Interesse und Vorkenntnissen der Hörerinnen und Hörer können auch Verzweigungsprozesse in stetiger Zeit behandelt werden.

Vorausgesetzt werden Kenntnisse wie sie z.B. in der Vorlesung Wahscheinlichkeitstheorie vermittelt werden. Vorkenntnisse über Martingale und Markovketten sind hilfreich, wir können aber benötigte Resultate aus diesen Gebieten auch kurz in der Vorlesung behandeln.

Literatur:

1.)
K. B. Athreya and P. E. Ney, Branching processes, Springer, 1972
2.)
P. Jagers, Branching processes with biological applications, Wiley, 1975
3.)
Weitere Literatur wird in der Vorlesung mitgeteilt
_________________________________________________________________________________________________________________________

Typisches Semester:  

7. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Wahrscheinlichkeitstheorie

Sprechstunde Dozent:  

Di 10–12 Uhr, Zi. 248, Eckerstr. 1

Sprechstunde Assistent:  

wird noch mitgeteilt

 
Abteilung für
Finanzmathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Futures and Options

  

Dozentin:  

Dr. E. A. v. Hammerstein

  

Zeit/Ort:  

Di 16–18 Uhr, HS 3219, KG III

  

Übungen:  

Mi 12–14 Uhr, HS 1221, KG I

  

Tutorium:  

Dr. E. A. v. Hammerstein

  

Web-Seite:  

http://www.finance.uni-freiburg.de

  
 
_______________________________________________________________

Inhalt:
The second revolution in mathematical finance following the Markowitz mean-variance theory of risk and return and the capital asset pricing model, concerns the option pricing theory of Black, Scholes and Merton from 1973 and the risk-neutral valuation theory that grew from it. In this course we introduce financial models in discrete as well as in continuous time and explain the basic principles of risk-neutral valuation of derivatives. Besides of futures and standard put and call options a number of more sophisticated derivatives is introduced as well. We also discuss interest-rate sensitive instruments such as caps, floors and swaps.
The course, which is taught in English, is offered for the second year in the Finance profile of the M.Sc. Economics program as well as for students of mathematics and M.Sc. Volkswirtschaftslehre.

Literatur:

1.)
Chance, D. M., Brooks, R.: An Introduction to Derivatives and Risk Management, 8th ed., South-Western, 2009
2.)
Hull, J. C.: Options, Futures, and other Derivatives, 7th ed., Prentice Hall, 2009
3.)
Strong, R. A.: Derivatives. An Introduction, 2nd ed., South-Western, 2004
_____________________

Typisches Semester:  

ab 6. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Vorlesung Stochastik

Prüfungsleistung:  

Klausur

Sprechstunde Dozent:  

n.V., Zi. 01010, Alte Universität, Bertholdstraße 17

 
PIC      
Abteilung für
Mathematische Logik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Set Theory of the Real Line

  

Dozent:  

Dr. Giorgio Laguzzi

  

Zeit/Ort:  

Di 14–16 Uhr, SR 125, Eckerstr. 1

  

Übungen:  

Do 10–12 Uhr, SR 404, Eckerstr. 1 oder n. V.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/giorgio

  
 
_______________________________________________________________

Inhalt:
 
The aim of this course is to give an introduction to the study of the real line from the set-theoretical viewpoint. When dealing with the real numbers, it is a common practice in set theory to work with the Baire space, i.e., the set of infinite sequences of natural numbers endowed with the Baire topology. As a consequence, one can investigate questions concerning measure and category in terms of combinatorial properties of infinite sequences and trees. We will develop a careful study of the ideals of null and meager sets, as well as the regularity properties, such as the Baire property, the Lebesgue measurability and the perfect set property, and we will further see the connections with infinite games.

Literatur:

1.)
Tomek Bartoszyński, Haim Judah, Set Theory of the Real Line, AK Peters, 1995
2.)
Kenneth Kunen, Set Theory, An Introduction to Independence Proofs, North Holland, 1980
3.)
Azriel Levy, Basic Set Theory, Springer, 1979
_____________________________________________________________

Typisches Semester:  

mittleres

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Mathematische Logik

Folgeveranstaltungen:  

Seminar über Forcing

Sprechstunde Dozent:  

Di, 13–14 Uhr, Zi. 311, Eckerstr. 1

 

 

2. Berufsorientierte Veranstaltungen

Mathematisches Institut
WS2014/15 PIC_________________________________________________________

Veranstaltung:  

Lernen durch Lehren

  

Dozent:  

Alle Dozentinnen und Dozenten von Vorlesungen

  

Teilnehmerliste:  

bis Vorlesungbeginn über das LSF belegen

  

Web-Seite:  

https://www.verwaltung.uni-freiburg.de/lsfserver/
und durchklicken: Vorlesungsverzeichnis → WS 2014 → Fakultät für Mathematik und Physik → Mathematik → Begleitveranstaltungen
  
 
_______________________________________________________________

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden im BSc- oder MSc-Studiengang Mathematik, die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Bitte belegen Sie die Veranstaltung über das LSF bis Vorlesungsbeginn, und zwar die Gruppe desjenigen Dozenten, bei dem Sie tutorieren.

Leistungsnachweis:

In Ermangelung eines passenden Wahlbereichs kann das Modul für Lehramtsstudierende in dieser Form zur Zeit nicht angeboten werden.__________________________________________________________

Typisches Semester:  

ab 5. Fachsemester

Kommentar:  

nur für BSc- oder MSc-Studiengang Mathematik; Tutorat zu einer Mathematik-Vorlesung im gleichen Semester ist notwendige Voraussetzung

ECTS-Punkte:  

3 Punkte

Studienleistung:  

siehe Text oben
 

Abteilung für
Didaktik der Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Didaktik der Algebra und Analysis

  

Dozent:  

Martin Kramer

  

Zeit/Ort:  

2-stündig zur Wahl: Mo 12–14 Uhr oder Di 12–14 Uhr
oder Di 14–16 Uhr; SR 404, Eckerstr. 1

  

Übungen:  

14-tgl. n.V.

  

Tutorium:  

Janna Meyer-Boye

  

Teilnehmerliste:  

Bitte belegen Sie Ihren Wunschtermin ab 1.8. und bis zum 12.10. über das elektronische Vorlesungsverzeichnis der Universität. Pro Gruppe gibt es 24 Plätze.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Die Vorlesungen über Didaktik bestehen aus zwei Teilen: Didaktik der Algebra und Analysis (WS) und Didaktik der Geometrie und Stochastik (SS).

Eine scharfe Abgrenzung der Einzelthemen ist im schulischen Kontext wenig hilfreich. So wird z. B. die Projektion auf den ersten Blick der Geometrie zugeordnet, andererseits entsteht durch die Projektion einer Drehbewegung die Sinus- bzw. Kosinusfunktion. Im Sinne einer ganzheitlichen und vernetzenden Didaktik werden in der Vorlesung viele Bezüge zwischen den einzelnen, innermathematischen Disziplinen geschaffen.

Erörtert werden didaktische Methoden der Geometrie und Stochastik, die didaktische Bedeutung des Materials im schulischen Kontext sowie die Bedeutung von kooperativem Lernen (Gruppenarbeit). Zentral ist der Wechsel zwischen symbolischen, ikonischen und enaktiven Repräsentationsebenen (nach Bruner). An konkreten Beispielen wird ein konstruktivistischer Vermittlungsansatz im Kontext der bildungsplanspezifischen Inhalte (lernen, begründen, problemlösen und kommunizieren) aufgezeigt.

Die Vorlesung legt Wert darauf, dass die dargestellte Didaktik konkret und interaktiv erlebt wird. Die Folge ist ein ständiger Rollenwechsel des Hörers: Einerseits erlebt er die Dinge aus der Schülerperspektive, auf der anderen Seite schlüpft er in die Rolle des reflektierenden Lehrers.

Literatur:

1.)
Büchter, A., Henn, H.-W.: Elementare Analysis – Von der Anschauung zur Theorie; Spektrum-Verlag
2.)
Danckwerts, R., Vogel, D.: Analysis verständlich unterrichten; Spektrum-Verlag
3.)
Kramer, M.: Mathematik als Abenteuer; Aulis Verlag
4.)
Padberg, F.: Didaktik der Arithmetik, BI Wissenschaftsverlag
5.)
Spektrum der Wissenschaft (Zeitschrift): Mathematische Unterhaltungen I–III; Spektrum-Verlag
6.)
Spitzer, Manfred: Geist im Netz – Modelle für Lernen, Denken und Handeln; Spektrum Akademischer Verlag, Heidelberg
7.)
Vollrath, H.-J.: Algebra in der Sekundarstufe; Spektrum-Verlag
_____________________________________

Typisches Semester:  

3. Semester

ECTS-Punkte:  

3 Punkte

Folgeveranstaltungen:  

Didaktik der Geometrie und Stochastik, Didaktik-Seminar

Sprechstunde Dozent:  

n.V., Zi. 131, Eckerstr. 1

 
Abteilung für
Didaktik der Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Robotik als Abenteuer – MINT

  

Dozent:  

Martin Kramer
  

Zeit/Ort:  

Mi 10–13 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

Julia Pflum, Marion Kessler

  

Teilnehmerliste:  

Interessenten sollen sich bitte in eine bei Frau Schuler ausliegende Liste eintragen, Zi. 132, Di–Do, 9–13 und 14–16:30 Uhr

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
MINT steht für die Vernetzung von Mathematik, Informatik, Naturwissenschaft und Technik. Robotik repräsentiert dabei alle vier Buchstaben gleichzeitig und eignet sich so wunderbar für die Schule im Rahmen einer AG oder von Projekttagen. Ein aktuelles Thema.

Das Seminar besteht aus zwei Teilen. Zuerst wird aus Fischertechnik ein mobiler Roboter gebaut und mit immer feineren Methoden mit der kindgerechten Software RoboPro programmiert.

Der zweite Teil besteht in der Durchführung eines zweitägigen Workshops (Freitagnachmittag bis Sonntagmorgen), der im Seminar geplant und von je zwei Teilnehmern in den Semesterferien durchgeführt wird.

Es sind keinerlei Vorkenntnisse erforderlich.____________________________________________________________

Typisches Semester:  

4.–8. Semester

ECTS-Punkte:  

4 Punkte

Folgeveranstaltungen:  

Fachdidaktik-Vorlesungen

Sprechstunde Dozent:  

n.V., Zi. 131, Eckerstr. 1

 
Abteilung für
Didaktik der Mathematik
WS2014/15 PIC_________________________________________________________

Vorlesung:  

Medieneinsatz im Mathematikunterricht

  

Dozent:  

Jürgen Kury

  

Zeit/Ort:  

Mi 14–16 Uhr, SR 127, Eckerstr. 1
und Mi 16–17 Uhr, SR 131, Eckerstr. 1

  

Teilnehmerliste:  

Interessenten sollen sich bitte in eine bei Frau Schuler ausliegende Liste eintragen, Zi. 132, Di–Do, 9–13 und 14–16:30 Uhr

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Der Einsatz von Unterrichtsmedien im Mathematikunterricht gewinnt sowohl auf der Ebene der Unterrichtsplanung wie auch der der Unterrichtsrealisierung an Bedeutung. Vor dem Hintergrund konstruktivistischer Lerntheorien zeigt sich, dass der reflektierte Einsatz unter anderem von Computerprogrammen die mathematische Begriffsbildung nachhaltig unterstützen kann. So erlaubt beispielsweise das Experimentieren mit Computerprogrammen mathematische Strukturen zu entdecken, ohne dass dies von einzelnen Routineoperationen (wie z. B. Termumformung) überdeckt würde. Es ergeben sich daraus tiefgreifende Konsequenzen für den Mathematikunterricht. Von daher setzt sich dieses Seminar zum Ziel, den Studierenden die notwendigen Entscheidungs- und Handlungskompetenzen zu vermitteln, um zukünftige Mathematiklehrer auf ihre berufliche Tätigkeit vorzubereiten.

Ausgehend von ersten Überlegungen zur Unterrichtsplanung werden anschließend Computer und Handheld hinsichtlich ihres jeweiligen didaktischen Potentials untersucht. Die dabei exemplarisch vorgestellten Systeme sind:

Jeder Studierende soll eine Unterrichtssequenz ausarbeiten, die gegebenenfalls während einer Unterrichtsstunde erprobt wird.____________________________________________________________________________

Typisches Semester:  

ab 1. Semester

ECTS-Punkte:  

4 Punkte

Nützliche Vorkenntnisse:  

Kenntnisse aus den Anfängervorlesungen

Studienleistung:  

Jeder Studierende soll eine Unterrichtssequenz ausarbeiten, die gegebenenfalls während einer Unterrichtsstunde erprobt wird.

Sprechstunde Dozentin:  

n.V., Didaktik, Eckerstr. 1

 
Abteilung für
Didaktik der Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Schulmathematische Themen mit Geogebra

  

Dozent:  

Dr. Gerhard Metzger

  

Zeit/Ort:  

Mo 14–17 Uhr, SR 131 (Didaktik-Vorraum), Eckerstr. 1

  

Tutorium:  

N. N.

  

Teilnehmerliste:  

Interessenten sollen sich bitte in eine bei Frau Schuler ausliegende Liste eintragen, Zi. 132, Di–Do, 9–13 und 14–16:30 Uhr

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Geogebra ist eine dynamische Geometriesoftware, die die Möglichkeiten von Computer- algebrasystemen und Dynamischer Geometriesoftware verbindet. Sie wird immer stärker auch im Unterricht eingesetzt.

In diesem Seminar sollen konkrete, unterrichtsrelevante Beispiele aus allen Jahrgangsstufen fachwissenschaftlich und fachdidaktisch aufgearbeitet werden. An ihnen werden Kenntnisse über den Einsatz von Geogebra vermittelt. Dabei wird auch stets der sinnvolle Einsatz von Geogebra thematisiert. Die Erstellung eigener Arbeitsblätter wird angestrebt.

Mögliche Themen sind z. B. der Einsatz von Geogebra im Geometrieunterricht, bei der Behandlung von Extremwert- und Optimierungsaufgaben, bei der Einführung von Ableitung und Integral und im Stochastikunterricht.____________________________________________________________________

Typisches Semester:  

ab dem 1. Semester

ECTS-Punkte:  

4 Punkte

Nützliche Vorkenntnisse:  

Kenntnisse aus den Anfängervorlesungen

Sprechstunde Dozent:  

n.V. per E-Mail an gerhard-metzger@t-online.de

 

PIC    

Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Prakt. Übung zu:  

Numerik (1. Teil der zweisemestrigen Veranstaltung)

  

Dozent:  

Prof. Dr. D. Kröner

  

Zeit/Ort:  

Mo, Di, Do 14–16 Uhr, Mi, Do 16–18 Uhr, CIP-Pool Raum 201, Hermann–Herder–Str. 10

  

Übungen:  

2-stündig (14-täglich) Termin zur Wahl im Rahmen der Kapazitäten

  

Tutorium:  

Christoph Gersbacher

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
In dieser praktischen Übung werden die in der Vorlesung Numerik besprochenen Algorithmen implementiert und an praktischen Beispielen getestet. Es findet 14-täglich abwechselnd mit den Übungen zur Vorlesung statt. Es sind Kenntnisse der Programmiersprache C erforderlich.______________________________________________________________________________________________________

Typisches Semester:  

3. Semester

ECTS-Punkte:  

für beide Teile zusammen 3 Punkte

Notwendige Vorkenntnisse:  

Grundvorlesungen in Linearer Algebra und Analysis

Sprechstunde Dozent:  

Mi 11–12 Uhr, Raum 215, Hermann–Herder–Str. 10

Sprechstunde Assistent:  

Di 10–11 Uhr, Raum 210, Hermann–Herder–Str. 10

 
PIC    
Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Prakt. Übung zu:  

Einführung in die Theorie und Numerik partieller Differentialgleichungen

  

Dozent:  

Prof. Dr. D. Kröner

  

Zeit/Ort:  

Mo 16–18 Uhr, SR 404, Eckerstr. 1

  

Tutorium:  

Tobias Malkmus

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
In den praktischen Übungen sollen die in der Vorlesung „Einführung in die Theorie und Numerik partieller Differentialgleichungen“ vorgestellten numerischen Verfahren zur Lösung partieller Differentialgleichungen implementiert werden. Ziel ist die Erstellung eines effizienten, selbstadaptiven Programmpakets zur Berechnung von Näherungslösungen elliptischer Differentialgleichungen mit Hilfe der Finite-Elemente-Methode. Programmierkenntnisse in C werden vorausgesetzt und im Rahmen der praktischen Übungen weiter ausgebaut. Zusätzlich findet eine Einführung in die in der Arbeitsgruppe verwendeten Programmpakete statt. Studierenden, die vorhaben, in der Angewandten Mathematik eine Zulassungs- oder Masterarbeit zu schreiben, wird die Teilnahme an den praktischen Übungen empfohlen.

Literatur:

1.)
D. Braess, Finite Elemente, Springer, Berlin (2007).
2.)
H. R. Schwarz, Methode der Finiten Elemente, Teubner, Stuttgart (1991).
3.)
G. Dziuk, Theorie und Numerik partieller Differentialgleichungen, De Gruyter (2010).
________

Typisches Semester:  

5. Semester

ECTS-Punkte:  

3 Punkte

Sprechstunde Dozent:  

Mi 11–12 Uhr, Raum 215, Hermann–Herder–Str. 10

Sprechstunde Assistent:  

Di 10–11 Uhr, Raum 210, Hermann–Herder–Str. 10

 
PIC    
Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Prakt. Übung zu:  

Theorie und Numerik partieller Differentialgleichungen I

  

Dozent:  

Prof. Dr. S. Bartels

  

Zeit/Ort:  

Mi 14–16 Uhr, CIP-Pool 201, Hermann-Herder-Str. 10

  

Tutorium:  

Dipl.-Math. P. Schreier

  

Web-Seite:  

http://aam.uni-freiburg.de/bartels

  
 
_______________________________________________________________

Inhalt:
In der praktischen Übung sollen die in der Vorlesung entwickelten und analysierten Verfahren praktisch umgesetzt und experimentell getestet werden. Dies wird mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse und Erfahrung im Umgang mit MATLAB werden vorausgesetzt.

Literatur:

1.)
D. Braess: Finite Elemente. Springer, 2007.
2.)
D. Boffi, F. Brezzi, M. Fortin: Mixed Finite Element Methods and Applications. Springer, 2013.
3.)
M. Dobrowolski: Angewandte Funktionalanalysis. Springer, 2005.
4.)
P. Knabner, L. Angermann: Numerical Methods for Elliptic and Parabolic PDEs. Springer, 2000.
5.)
C. Grossmann, H.-G. Roos: Numerische Behandlung partieller Differentialgleichungen. Springer, 2005.
_____________________________________________________________________________________________________

Typisches Semester:  

7. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Vorlesung Theorie und Numerik partieller Differerentialgleichungen I (parallel)

Sprechstunde Dozent:  

Mi 12–13 Uhr und n.V., Zimmer 209, Hermann-Herder-Str. 10

Sprechstunde Assistent:  

Wird in der Vorlesung bekannt gegeben

 
 
3. Seminare

PIC    

Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Proseminar:  

Numerik

  

Dozent:  

Prof. Dr. S. Bartels
  

Zeit/Ort:  

Mi 16–18 Uhr, SR 226, Hermann-Herder-Str. 10

  

Tutorium:  

Dipl.-Math. A. Papathanassopoulos

  

Vorbesprechung:  

Mo, 21.07.2014, 13:30 Uhr, SR 216, Hermann-Herder-Str. 10

  

Teilnehmerliste:  

Bei Frau Ruf, Zi. 205, Hermann-Herder-Str. 10

  

Web-Seite:  

http://aam.uni-freiburg.de/bartels

  
 
_______________________________________________________________

Inhalt:
Im Proseminar sollen weiterführende Themen der Numerik wie die Lösung großer linearer Gleichungssysteme, die Behandlung von Bézier-Kurven und die Lösung restringierter Optimierungsprobleme diskutiert werden.

Literatur:

1.)
R. Plato: Numerische Mathematik kompakt. Vieweg, 2006
2.)
R. Schaback, H. Wendland: Numerische Mathematik. Springer, 2004.
3.)
J. Stoer, R. Bulirsch: Numerische Mathematik I, II. Springer, 2007, 2005.
4.)
M. Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Vieweg+Teubner, 2006.
5.)
C. Geiger, C. Kanzwow: Theorie und Numerik restringierter Optimierungsaufgaben. Springer 2002.
__________________________________________________________________________________________________________________

Typisches Semester:  

5. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Grundvorlesungen Lineare Algebra und Analysis, Vorlesung Numerik

Studienleistung:  

Regelmäßige Teilnahme

Prüfungsleistung:  

Vortrag und zweiseitige Ausarbeitung

Sprechstunde Dozent:  

Mi 12–13 Uhr und n.V., Zimmer 209, Hermann-Herder-Str. 10

Sprechstunde Assistent:  

Wird in der Vorbesprechung bekannt gegeben

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Proseminar:  

Symmetrische Funktionen

  

Dozentin:  

Prof. Dr. K. Wendland

  

Zeit/Ort:  

Di 14–16 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

PD E. Scheidegger

  

Vorbesprechung:  

Mo 21.07.2014, 12–13 Uhr, SR 127, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/mathphys/lehre/WiSe14/SymmetrischeFunktionen.html

  
 
_______________________________________________________________

Inhalt:
Ein symmetrisches Polynom ist ein Polynom in n Variablen, welches invariant unter Permutationen der Variablen ist. Symmetrische Polynome treten natürlich in der Beziehung zwischen den Nullstellen eines Polynoms in einer Variable und seinen Koeffizienten auf. Nach dem Satz von Vieta sind die Koeffizienten dieses Polynoms wiederum Polynome in den Nullstellen, wobei die Reihenfolge der Nullstellen keine Rolle spielt. Dies führt auf die elementar–symmetrischen Polynome, die eine fundamentale Rolle spielen, da alle symmetrischen Polynome durch Linearkombinationen von elementar-symmetrischen ausgedrückt werden können.

Unabhängig davon bilden die symmetrischen Polynome interessante Strukturen. Wir werden weitere ausgezeichnete symmetrische Polynome, wie z. B. die Schurpolynome kennenlernen. Deren Multiplikation kann mit Hilfe von Young–Tableaux grafisch dargestellt werden:

Die Verallgemeinerung auf unendlich viele Variablen führt zum Ring der symmetrischen Funktionen, welcher eine zentrale Rolle in der Kombinatorik und in der Darstellungstheorie spielt.

Literatur:

1.)
I.G. Macdonald, Symmetric Functions and Hall Polynomials, Oxford Science Publications, 2nd ed., 1995
________________________________________________________________________

Typisches Semester:  

ab 3. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Lineare Algebra

Sprechstunde Assistent:  

Mi 16–17 Uhr, Raum 329, Eckerstr. 1

 
PIC
WS2014/15 PIC_________________________________________________________

Proseminar:  

Kombinatorik

  

Dozent:  

Prof. Dr. Hans Rudolf Lerche
  

Zeit/Ort:  

Di 16–18 Uhr, SR 125, Eckerstr. 1

  

Tutorium:  

N. N.

  

Vorbesprechung:  

Do 31.07.2014, 13:30 Uhr, Zi. 232, Eckerstr. 1
  

Teilnehmerliste:  

Eintrag in eine Liste im Sekretariat der Stochastik (Zi. 226 bzw. 245, Eckerstr. 1) ab 01. Juli bis zum 29. Juli 2014

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de

  
 
_______________________________________________________________

Inhalt:
 
Das Proseminar behandelt einige grundlegende Ergebnisse der Kombinatorik. Zum Beispiel geht es um Abzählen. Es zeigt sich aber schnell, dass Zählen oft schwerer ist, als man zunächst glaubt. Man sieht dies an folgendem (von Reverend Kirkman 1851 formuliertem) Problem:
Man führe 15 Schulmädchen an 7 Sonntagen in jeweils 5 Dreierreihen so spazieren, dass jedes Paar an genau einem Sonntag in einer Reihe zusammentrifft. Wie viele Möglichkeiten gibt es?
Der besondere Reiz der Kombinatorik besteht darin, dass man mit elementaren Hilfsmitteln bei einfach zu formulierenden Fragen bereits zu tiefen Resultaten gelangen kann.
Eine Einführung zu der Frage „Wie halte ich einen mathematischen Vortrag“ wird in der Vorbesprechung gegeben.

Literatur:

1.)
Aigner, M.; Ziegler, G. M.; Hofmann, K. H.: Das Buch der Beweise, Springer 2009 (2. Aufl.)
2.)
Cameron, P.: Combinatorics. Cambridge: Cambridge University Press 1996
3.)
Jacobs, K. und Jungnickel, D.: Einführung in die Kombinatorik. Berlin: De Gruyter 2003 (2. Aufl.)
___________________________________________________________________________________________________________

Typisches Semester:  

5. Semester

Notwendige Vorkenntnisse:  

Analysis I und Lineare Algebra I

Sprechstunde Dozent:  

Di, 11–12 Uhr, Zi. 233, Eckerstr. 1

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Proseminar:  

Mathematik im Alltag

  

Dozenten:  

Prof. Dr. V. Bangert, Prof. Dr. S. Goette

  

Zeit/Ort:  

Mo 10–12 Uhr, Di 14–16 Uhr, SR 125; Mi 16–18 Uhr, SR 403, Eckerstr. 1

  

Beginn:  

07.01.2015

  

Tutorium:  

Anja Fuchshuber

  

Vorbesprechung:  

Di 22.07.2014, 13:00–14:00 Uhr, SR 404, Eckerstr. 1

  

Teilnehmerliste:  

Bei Sabine Keim, Mo–Fr 9–12 Uhr, Raum 341, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/goette/

  
 
_______________________________________________________________

Inhalt:
Im täglichen Leben spielt Mathematik eine ähnlich wichtige Rolle wie andere Wissenschaften. Sie hilft, Probleme aus verschiedensten Bereichen zu beschreiben, zu verstehen, und oft auch zu lösen. Sie ist die Basis für viele technische Errungenschaften des modernen Lebens. Für den Laien ist das in den meisten Fällen nicht erkennbar, da der mathematische Hintergrund oberflächlich in der Regel nicht sichtbar ist.

Beispiele hierfür sind Probleme der Datenverarbeitung (CD-Spieler, Handys, Online-Banking), oder aber technische Geräte wie Navigationssysteme (Standortbestimmung, Routenplanung). Auch in den Gesellschaftswissenschaften spielt Mathematik eine Rolle, beispielsweise Spieltheorie in den Wirtschaftswissenschaften.

In den Vorträgen soll es darum gehen, einzelne Anwendungen zunächst vorzustellen, das zugrundeliegende mathematische Problem herauszuarbeiten und dann seine Lösung zu präsentieren. Die angegebene Literatur dient dabei nur als erster Anhaltspunkt, weitere Quellen sollen die Teilnehmerinnen und Teilnehmer selbst finden.

Eigene Themenvorschäge der Teilnehmerinnen und Teilnehmer sind willkommen, sofern sie in den Rahmen des Proseminars passen. In diesem Fall bitten wir, rechtzeitig vor der Vorbesprechung mit einem der Dozenten Kontakt aufzunehmen.

Literatur:

1.)
M. Aigner, E.Behrends, Alles Mathematik. Von Pythagoras zum CD-Spieler, Vieweg, 2000
__

Typisches Semester:  

5. (nach dem Praxissemester)

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Anfängervorlesungen; für einzelne Vorträge sind weiterführende Vorlesungen erforderlich, siehe Programm

Studienleistung:  

Regelmäßige Teilnahme

Prüfungsleistung:  

Vortrag

Sprechstunde Dozenten:  

V. Bangert: Di 14:15–15:00 Uhr, Zi. 335, Eckerstr. 1, S. Goette: Mi 13:10–13:55 Uhr, Zi. 340, Eckerstr. 1

Sprechstunde Assistentin:  

Do 9–12 Uhr, Zi. 325, Eckerstr. 1

Kommentar:  

Dieses Proseminar richtet sich in erster Linie an Studierende des Lehramts

 

Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Spezielle Holonomie

  

Dozenten:  

Dr. A. Degeratu, Prof. Dr. S. Goette

  

Zeit/Ort:  

Mo 14–16 Uhr, SR 125, Eckerstr. 1

  

Tutorium:  

Dr. Anda Degeratu

  

Vorbesprechung:  

Mo 28.07.2014, 13:15 Uhr, SR 414, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/degeratu/

  
 
_______________________________________________________________

Inhalt:
In der Riemannschen Geometrie liefert Parallelverschiebung entlang von Schleifen an x ∈ M eine Gruppe von Isometrien des Tangentialraums TxM, die Holonomiegruppe. Wenn die universelle Überlagerung von M weder ein Riemannsches Produkt noch ein symmetrischer Raum ist, kommen nach einem Resultat von Berger nur noch die Gruppen SO(n), U(k), SU(k) (dim M = n = 2k), Sp(ℓ) ⋅ S1, Sp(ℓ) (n = 4ℓ), G 2 (n = 7) und Spin(7) (n = 8) in Frage. Dabei ist die Gruppe SO(n) der generische Fall; alle anderen bezeichnet man als spezielle Holonomiegruppen.

Je kleiner die Holonomiegruppe ist, desto mehr parallele Strukturen trägt M. So besitzt TM für Mannigfaltigkeiten mit Holonomie U(k), SU(k) oder Sp(ℓ) eine parallele komplexe Struktur, im Fall Sp(ℓ) sogar eine quaternionische. Von speziellem Interesse in Mathematik und Physik sind beispielsweise Calabi-Yau-Mannigfaltigkeiten (Holonomie SU(k)) sowie G2-Mannigfaltigkeiten.

Während sich Calabi-Yau-Mannigfaltigkeiten mit geometrischen und algebraischen Methoden gut studieren lassen, wurden kompakte Mannigfaltigkeiten mit Holonomie G2 und Spin(7) erst von Joyce konstruiert. In diesem Seminar wollen wir spezielle Eigenschaften sowie die Joyce-Konstruktion von G2-Mannigfaltigkeiten kennenlernen. Dazu beginnen wir der verwandten, aber etwas einfacheren Kummer-Konstruktion von K3-Flächen, das heißt, von kompakten 4-Mannigfaltigkeiten mit Holonomie SU(2) = Sp(1).

Literatur:

1.)
D. Joyce: Compact Manifolds of Special Holonomy. Oxford University Press, Oxford, 2000.
_

Typisches Semester:  

1.–3. Semester Master

ECTS-Punkte:  

B.Sc.: 4 Punkte; M.Sc.: 6 Punkte

Notwendige Vorkenntnisse:  

Differentialgeometrie (Riemannsche Geometrie)

Nützliche Vorkenntnisse:  

Komplexe Geometrie, Analysis elliptischer Differentialgleichungen

Studienleistung:  

Regelmäßige Anwesenheit

Prüfungsleistung:  

Vortrag

Sprechstunde Dozenten:  

A. Degeratu: Mo 13–14 Uhr, Zi. 328, Eckerstr. 1 S. Goette: Mi 13:10–13:55 Uhr, Zi 340, Eckerstr. 1

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Endliche algebraische Gruppen

  

Dozentin:  

Prof. Dr. Annette Huber-Klawitter

  

Zeit/Ort:  

Di 12–14 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

Dr. Fritz Hörmann

  

Vorbesprechung:  

Mi 23.07.2014, 13:00 (!) Uhr, SR 218, Eckerstr.1

  

Teilnehmerliste:  

bei Frau Frei, Raum 433, Eckerstr. 1

  
 
_______________________________________________________________

Inhalt:
Eine interessante Klasse von affinen Varietäten sind solche, die zusätzlich eine Gruppenstruktur tragen. Dabei fordert man, dass die Multiplikationsabbildung G × G → G und die Inversenbildung G → G Morphismen von Varietäten (also durch Polynome gegeben) sind. Die zugehörigen Koordinatenringe nennt man Hopfalgebren. Sie sind hochsymmetrische Objekte und haben eine interessante Theorie, insbesondere in dem Fall, dass sie endliche k-Algebren sind. Überraschenderweise können die Hopfalgebren in diesem Fall durch einfache lineare Algebra beschrieben werden, selbst wenn man darauf verzichtet, den Grundkörper als algebraisch abgeschlossen anzunehmen.

Dieser schöne und wichtige Zusammenhang ist jedoch recht tiefliegend und ihn zu verstehen wird das Hauptziel des Seminares sein. Er ist der Ausgangspunkt für eine ganze Reihe moderner Theorien in der arithmetischen algebraischen Geometrie, wie z. B. der p-adischen Hodgetheorie, außerdem spielt er eine tragende Rolle in der Klassifikation sogenannter elliptischer Kurven und abelscher Varietäten.

Literatur:

1.)
R. Pink, Finite Group Schemes, Vorlesungsskript,
http://www.math.ethz.ch/~pink/FiniteGroupSchemes.html
2.)
J. Stix, A course on finite flat group schemes and p-divisible groups, Vorlesungsskript,
http://www.math.uni-frankfurt.de/~stix/skripte/STIXfinflatGrpschemes20120918.pdf
3.)
W. C. Waterhouse, Introduction to Affine Group Schemes, Springer, 1979
4.)
J. S. Milne, Basic Theory of Affine Group Schemes, http://www.jmilne.org/ (vor allem Kapitel XII)
5.)
R. Schoof, Introduction to finite flat group schemes, http://homepages.uni-regensburg.de/~nan25776/schoof_introp_to_finite_flat_group_schemes.pdf
_____________________________________________________________________________

Typisches Semester:  

ab 5. Semester

Notwendige Vorkenntnisse:  

Kommutative Algebra, Algebra und Zahlentheorie

Studienleistung:  

Regelmäßige Teilnahme

Prüfungsleistung:  

Halten eines Vortrags

Sprechstunde Dozentin:  

Di 11–12 Uhr und n.V., Raum 434, Eckerstr. 1

Kommentar:  

Die Veranstaltung ist als Bachelor-Seminar geeignet

 
PIC    
Abteilung für
Angewandte Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Stochastische Differentialgleichungen

  

Dozenten:  

Prof. Dr. D. Kröner, Prof. Dr. P. Pfaffelhuber

  

Zeit/Ort:  

Mi 14–16 Uhr, SR 226, Hermann–Herder-Str. 10

  

Tutorium:  

Johannes Daube

  

Vorbesprechung:  

Mo 21.07.2014, 14:00 Uhr, Zi. 227, Hermann-Herder-Str. 10

  

Teilnehmerliste:  

bei Frau Ruf, Sekretariat der Abt. für Angewandte Math., Zi. 205, Hermann-Herder-Str. 10. Eintragungen sind ab sofort möglich.

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
Viele in der Natur auftretende Phänomene, z. B. Wachstumsprozesse, werden durch gewöhnliche Differentialgleichungen modelliert, deren Lösung im Allgemeinen durch eine glatte Lösung gegeben ist. Die Messergebnisse zu dem entsprechenden realen Experiment sind allerdings oft durch eine nicht glatte Funktion, vielmehr durch eine zittrige Kurve gegeben. Ziel ist es, die gewöhnlichen Differentialgleichungen so zu „manipulieren“, dass ihre Lösungen mit der zittrigen Kurve besser übereinstimmen. Dies führt zum Konzept von stochastischen Differentialgleichungen.

Ziel des Seminars ist es, eine Einführung in die Theorie und – wenn es die Zeit erlaubt – die Numerik stochastischer Differentialgleichungen zu geben. Vorkenntnisse aus der Stochastik (z. B. aus der Vorlesung Wahrscheinlichkeitstheorie) und der Theorie und Numerik für partielle Differentialgleichungen sind wünschenswert.

Literatur:

1.)
L. C. Evans, An Introduction to Stochastic Differential Equations
2.)
P. Kloeden, E. Platen, Numerikcal Solution of Stochastic Differential Equations
________________

Typisches Semester:  

ab dem 5. Semester

Sprechstunde Dozenten:  

Prof. Kröner, Mi 11–12 Uhr, Zi. 215, Hermann–Herder-Str. 10 Prof. Pfaffelhuber, Fr 16–17 Uhr, Raum 241, Eckerstr. 1

Sprechstunde Assistent:  

Mi, 16–17 Uhr und n. V., Zi. 212, Hermann–Herder–Str. 10

 
PIC      
Abteilung für
Mathematische Logik
WS2014/15 PIC_________________________________________________________

Seminar:  

Mengenlehre: Forcingaxiome

  

Dozentin:  

Heike Mildenberger

  

Zeit/Ort:  

Di 16–18 Uhr, SR 318, Eckerstr. 1

  

Übungen:  

2-stündig, nach Vereinbarung

  

Tutorium:  

N. N.

  

Vorbesprechung:  

Montag, 21.07.2014, 13 Uhr, Raum 310, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/mildenberger/veranstaltungen/ws14/forcingseminar.html

  
 
_______________________________________________________________

Inhalt:

Der Baire’sche Kategoriensatz sagt:

„In einem vollständigen metrischen Raum ist der Schnitt abzählbar vieler offener dichter Mengen dicht.“

Mit Hilfe dieses Satzes lassen sich Existenzbeweise führen. Martins Axiom, das bekannteste Forcingaxiom, ist konsistent relativ zu ZFC und kann als Variation der Baire’schen Aussage verstanden werden:

„In jeder Halbordnung mit höchstens abzählbaren Antiketten ist der Schnitt ℵ1 vieler offener dichter Mengen dicht.“

In diesem Seminar werden wir Forcingaxiome im Hinblick auf ihre relative Konsistenz und auf ihre Konsequenzen hin untersuchen. Das Thema ist für Masterarbeiten geeignet.

Literatur:

1.)
Todorcevic, Stevo, Notes on forcing axioms, World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2014
____________________________________________________________________________________________

Typisches Semester:  

mittleres

Notwendige Vorkenntnisse:  

Mathematische Logik, Unabhängigkeitsbeweise

Studienleistung:  

Vortrag

Prüfungsleistung:  

Vortrag

Sprechstunde Dozentin:  

Di 13–14 Uhr, Raum 310, Eckerstr. 1

 
PIC
WS2014/15 PIC_________________________________________________________

Seminar:  

Finanzmathematik

  

Dozent:  

Prof. Dr. L. Rüschendorf
  

Zeit/Ort:  

Mi 16–18 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

B. Köpfer

  

Vorbesprechung:  

Mi 16.07.2014, 13:00 Uhr, Zi. 232, Eckerstr. 1

  

Teilnehmerliste:  

Bitte tragen Sie sich bis zum 14.07.2014 in eine Liste ein, die im Sekretariat der Stochastik (Zi. 226 oder Zi. 245) ausliegt.

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/Vorlesungen

  
 
_______________________________________________________________

Inhalt:
 
In dem Seminar werden Themen aus der stochastischen Integration und Finanzmathematik erweitert und vertieft. Thema sind z. B. Portfolio-Optimierung, Tanaka-Formel und Lokalzeit, Hedgen von Derivaten und Unvollständige Märkte.__________________________________________________

Typisches Semester:  

ab 3. Semester im Master

Notwendige Vorkenntnisse:  

Vorlesung Stochastische Integration und Finanzmathematik

Sprechstunde Dozent:  

Mi 11–12 Uhr, Zi. 242, Eckerstr. 1

Sprechstunde Assistent:  

Mi 10–11 Uhr, Zi. 227, Eckerstr. 1

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Spiegelungsgruppen

  

Dozent:  

Prof. Dr. W. Soergel, P. Pandžić (voraussichtlich)

  

Zeit/Ort:  

Fr 8–10 Uhr, SR 404, Eckerstr. 1

  

Tutorium:  

A. Sartori

  

Vorbesprechung:  

Fr 18.07.2014, 9:00 Uhr s.t., SR 404, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/soergel/SeminarSpieg1415.html

  
 
_______________________________________________________________

Inhalt:
Dieses Seminar richtet sich an Studierende im Bachelorstudiengang sowie an Studierende im Lehramtsstudiengang.

Das Seminar soll in die Theorie endlicher und affiner Spiegelungsgruppen einführen. Eine Spiegelungsgruppe ist eine Gruppe von Bewegungen eines euklidischen Raumes, die durch Spiegelungen erzeugt wird.

Wir werden unter anderem die endlichen Spiegelungsgruppen klassifizieren, eine Darstellung durch Erzeugende und Relationen herleiten, und die Ringe der invarianten Polynomfunktionen studieren.

Literatur:

1.)
James E. Humphreys: Finite reflection groups
2.)
N. Bourbaki: Lie 4-6
3.)
W. Soergel: Skript „Spiegelungsgruppen und Wurzelsysteme“
_______________________________________

Typisches Semester:  

3.–5. Semester

Notwendige Vorkenntnisse:  

Lineare Algebra I und II, Algebra

Sprechstunde Dozent:  

Do 11:30–12:30 Uhr, Zi. 429, Eckerstr. 1

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Semisimple Lie Algebras

  

Dozent:  

Pavle Pandžić (voraussichtlich)

  

Zeit/Ort:  

Mo 14–16 Uhr, SR 218, Eckerstraße 1

  

Tutorium:  

N. N.

  

Vorbesprechung:  

Fr 25.07.2014, 9:00 s.t., SR 404, Eckerstraße 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/pandzic/Seminar.html

  
 
_______________________________________________________________

Inhalt:
This will be an introductory seminar on complex semisimple Lie algebras. It will underpin the course on Harish–Chandra modules with foundational material, but is also a central chapter of Lie theory in itself. We will take the text of Humphreys as a guideline.

Literatur:

1.)
J. E. Humphreys, Introduction to semisimple Lie algebras and representation theory, Springer

Typisches Semester:  

5. Semester

Notwendige Vorkenntnisse:  

Lineare Algebra

Nützliche Vorkenntnisse:  

Algebra und Zahlentheorie (vor Galoistheorie), Kommutative Algebra

Folgeveranstaltungen:  

Bei genügend Interesse weiterführendes Seminar.

Kommentar:  

Die Veranstaltung wird auf Englisch abgehalten. Sie ist gut geeignet, um Arbeiten bei Prof. Soergel vorzubereiten.

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Das Eigenwertproblem

  

Dozent:  

Prof. Dr. Wang

  

Zeit/Ort:  

Mi 16–18 Uhr, SR 125, Eckerstr. 1

  

Tutorium:  

C. Ketterer

  

Vorbesprechung:  

Do 24.07.2014, 14–16 Uhr, SR 414, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/wang

  
 
_______________________________________________________________

Inhalt:
 

In der Analysis und Numerik spielt das Eigenwertproblem eine wesentliche Rolle. In dem Seminar untersuchen wir verschiedene Eigenwertprobleme. Wir fangen von Sturm-Liouvilleschem Eigenwertproblem an. Weiter wollen wir verschiedene Probleme über den ersten Eigenwert des Laplace-Operators ausführlich betrachten.

1. Sturm-Liouvilleschem Eigenwertproblem
2. Eigenwerte des Laplace-Operators, Rayleigh-Ritz-Ungleichung
3. Faber-Krahn-Ungleichung des ersten Eigenwert des Laplace-Operators
4. Szegö-Weinberger-Ungleichung
5. Payne-Pólya-Weinberger-Ungleichung
6. . . .______________________________________________________________________________________________________________

Typisches Semester:  

ab 5. Semester

Notwendige Vorkenntnisse:  

Analysis III

Sprechstunde Dozent:  

Mi 10:30–11:30 Uhr, Zi. 210, Eckerstr. 1

Sprechstunde Assistent:  

wird in der Vorlesung mitgeteilt

 
PIC
WS2014/15 PIC_________________________________________________________

Seminar:  

Geometrie

  

Dozent:  

PD Dr. Dr. Heinz Weisshaupt
  

Zeit/Ort:  

Blockseminar, Termin nach Absprache

  

Vorbesprechung:  

Di 29.07.2014, 14:15 Uhr, SR 119, Eckerstrasse 1

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:

Das Seminar behandelt Fragestellungen der konvexen Geometrie.

Trotz der Einfachheit der Definition einer konvexen Menge – wir nennen eine Teilmenge eines Vektorraumes konvex, wenn diese mit je zwei ihrer Punkte auch deren Verbindungsstrecke enthält – ist das Gebiet der konvexen Geometrie ausgesprochen reichhaltig und viele relativ elementare Resultate sind doch tiefliegend und besitzen überraschende Anwendungen.

Das Seminar bietet einen Einstieg in das Gebiet. Vorkenntnisse in konvexer Geometrie sind nicht erforderlich.

Auf Wunsch kann auch ein Proseminar oder zweites Seminar aus einem benachbarten Gebiet (metrische Geometrie oder geometrische Topologie) angeboten werden.

Literatur:

Wird in der Vorbesprechung bekannt gegeben
_____________________________________________________________

Typisches Semester:  

ab dem 5. Semester geeignet; auch für höhere Semester

Notwendige Vorkenntnisse:  

Analysis, Lineare Algebra

Sprechstunde Dozent:  

Nach Vereinbarung

 
Abteilung für
Didaktik der Mathematik
WS2014/15 PIC_________________________________________________________

Seminar:  

Statistische Modelle in der klinischen Epidemiologie

  

Dozent:  

Prof. Martin Schumacher

  

Zeit/Ort:  

Mi 10:00–11:30 Uhr, HS Med. Biometrie und Med. Informatik, Stefan-Meier-Str. 26

  

Vorbesprechung:  

Vorbesprechung mit Hinweisen auf einführende Literatur: Mi, 30.07.2014, 11:30–12:30 Uhr, Konferenzraum IMBI, Stefan-Meier-Str. 26

  

Teilnehmerliste:  

Vorherige Anmeldung per email (sec@imbi.uni-freiburg.de) ist erwünscht.

  

Web-Seite:  

http://portal.uni-freiburg.de/imbi/lehre/wintersemester/Hauptseminar/

  
 
_______________________________________________________________

Inhalt:
Moderne statistische Methoden und Modellierungstechniken im Bereich der Biostatistik adressieren komplexe Fragestellungen in den biomedizinischen Wissenschaften, wie z. B. die Einbeziehung molekularer Information in Studien zur Ätiologie, Diagnose/Prognose und Therapie. Eine Auswahl solcher Problemstellungen soll in den Seminarvorträgen vorgestellt werden, die sich an kürzlich erschienenen Originalarbeiten orientieren; die genaue thematische Ausrichtung wird noch festgelegt.

Zu Beginn des Seminars werden ein oder zwei Übersichtsvorträge stehen, die als vertiefende Einführung in die Thematik dienen.

Das Hauptseminar ist terminlich und inhaltlich mit dem Oberseminar „Medizinische Statistik“ abgestimmt.

Literatur wird in der Vorbesprechung bekannt gegeben.

Das Seminar beginnt am 22.10.2014 und endet mit dem 11.02.2015._____________________________

Typisches Semester:  

Für Masterstudent(inn)en

Notwendige Vorkenntnisse:  

gute Kenntnisse in Wahrscheinlichkeitstheorie und Mathematischer Statistik

Sprechstunde Dozent:  

n.V.

 

 

4. Oberseminare, Projektseminare

und Kolloquien

Mathematisches Institut
WS2014/15 PIC_________________________________________________________

Lesekurs:  

„Wissenschaftliches Arbeiten“

  

Dozent:  

Alle Dozentinnen und Dozenten des Mathematischen Instituts

  

Zeit/Ort:  

nach Vereinbarung

  
 
_______________________________________________________________

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann.

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe (einem Oberseminar, Projektseminar . . .)) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im Vertiefungsmodul wird der Stoff des Lesekurses in der mündlichen Abschlussprüfung zusammen mit dem weiteren Stoff abgeprüft.__________________________________

Typisches Semester:  

9. Fachsemester, unmittelbar vor der Master-Arbeit

Kommentar:  

Teil des Vertiefungsmoduls im Master-Studiengang

Notwendige Vorkenntnisse:  

hängen vom einzelnen Lesekurs ab

Studienleistung:  

wird vom Betreuer festgelegt

Prüfungsleistung:  

Das Vertiefungsmodul wird mit einer mündlichen Prüfung über u.a. den Stoff des Lesekurses abgeschlossen.

 
Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Projektseminar:  

Seminar des Graduiertenkollegs

  

Dozent:  

Die Dozenten des Graduiertenkollegs

  

Zeit/Ort:  

Mi 14:00–16:00 Uhr, SR 404, Eckerstr. 1

  

Web-Seite:  

http://www.gk1821.uni-freiburg.de

  
 
_______________________________________________________________

Inhalt:
We are studying a subject within the scope our Graduiertenkolleg “Cohomological Methods in Geometry”: algebraic geometry, arithmetic geometry, representation theory, differential topology or mathematical physics or a mix thereof.

The precise topic will be chosen at the end of the preceeding semester. The program will be made available via our web site.

The level is aimed at our doctoral students. Master students are very welcome to participate as well. ECTS points can be gained as in any other seminar. For enquiries, see Prof. Dr. A. Huber-Klawitter or any other member of the Graduiertenkolleg._________________________________

Typisches Semester:  

ab 7. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

je nach Thema, meist algebraische Geometrie
 

Abteilung für
Reine Mathematik
WS2014/15 PIC_________________________________________________________

Forschungseminar:  

Internationales Forschungsseminar
Algebraische Geometrie

  

Dozent:  

Prof. Dr. Stefan Kebekus

  

Zeit/Ort:  

zwei Termine pro Semester, n.V., IRMA – Strasbourg,
siehe Website

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/kebekus/ACG/

  
 
_______________________________________________________________

Inhalt:
The Joint Seminar is a research seminar in complex and algebraic geometry, organized by the research groups in Freiburg, Nancy and Strasbourg. The seminar meets roughly twice per semester in Strasbourg, for a full day. There are about four talks per meeting, both by invited guests and by speakers from the organizing universities. We aim to leave ample room for discussions and for a friendly chat.

The talks are open for everyone. Contact one of the organizers if you are interested in attending the meeting. We have some (very limited) funds that might help to support travel for some junior participants.____________________________________________________________________________________________

Typisches Semester:  

Endphase des Haupt- oder Masterstudiums

Sprechstunde Dozent:  

n.V., Zi. 432, Eckerstr. 1

 

Mathematisches Institut

WS2014/15 PIC_________________________________________________________

Veranstaltung:  

Kolloquium der Mathematik

  

Dozent:  

Alle Dozenten der Mathematik

  

Zeit/Ort:  

Do 17:00 Uhr, HS II, Albertstr. 23 b

  
 
_______________________________________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17:00 Uhr im Hörsaal II in der Albertstr. 23 b statt.

Vorher gibt es um 16:30 Uhr im Sozialraum 331 in der Eckerstraße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/

 

 

 

Impressum
Herausgeber:
Mathematisches Institut
Eckerstr. 1
79104 Freiburg
Tel.: 0761-203-5534
E-Mail: institut@math.uni-freiburg.de

[prev] [prev-tail] [front] [up]