11.3 Fourierreihen
_____________________________________________________________________
Inhalt:
Das Proseminar beschäftigt sich mit der Theorie und Anwendungen von
Fourierreihen. Die Fourier-Reihe ist definiert für periodische Funktionen
und ist die Entwicklung dieser Funktionen nach dem Funktionensystem
cos(kx), sin(kx), für k 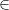 ℕ. Im Unterschied zu den Taylor-Reihen können
durch Fourier-Reihen auch periodische Funktionen dargestellt werden, die
nur stückweise stetig differenzierbar sind und deren Ableitungen
Sprungstellen haben.
ℕ. Im Unterschied zu den Taylor-Reihen können
durch Fourier-Reihen auch periodische Funktionen dargestellt werden, die
nur stückweise stetig differenzierbar sind und deren Ableitungen
Sprungstellen haben.
Nach der Definition für klassische Funktionen wird uns die Untersuchung
der Konvergenzeigenschaften zu einer natürlicheren Klasse von Funktionen
führen, den quadrat-integrablen. Definierbar sind Fourierreihen auch für
integrable Funktionen, jedoch sind die Konvergenzfragen wesentlich
schwieriger zu beantworten.
Anwendung findet die Theorie in partiellen Differentialgleichungen und der
Informationstheorie. Wir werden als Beispiel die Wellengleichung
betrachten und das Shannon Sampling Theorem beweisen. Dieser Satz
beantwortet die Frage: Kann ich aus dem Messsignal das Originalsignal
wiederherstellen? Schließlich wird die Fast Fourier Transform behandelt, die
eine schnelle numerische Berechung der Fourierreihe ermöglicht.
Zu den vorgestellten Themen gibt es unzählige Bücher. Von den
Teilnehmern wird eine selbständige Literaturrecherche erwartet.________
Typisches Semester: | ab 3. Semester |
ECTS-Punkte: | 3 |
Studienschwerpunkt: | Reine Mathematik, insbes. Analysis |
Notwendige Vorkenntnisse: | Analysis I, II, Lineare Algebra I, II |
Studienleistung: | Vortrag |
Sprechstunde Dozent: | Mi, 16–17 Uhr, Zi. 206, Eckerstr. 1 |
| |
Seminare
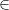 ℕ. Im Unterschied zu den Taylor-Reihen können
durch Fourier-Reihen auch periodische Funktionen dargestellt werden, die
nur stückweise stetig differenzierbar sind und deren Ableitungen
Sprungstellen haben.
ℕ. Im Unterschied zu den Taylor-Reihen können
durch Fourier-Reihen auch periodische Funktionen dargestellt werden, die
nur stückweise stetig differenzierbar sind und deren Ableitungen
Sprungstellen haben.