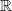[prev] [prev-tail] [tail] [up]

1.15 Das Willmore-Integral

Vorlesung:

Das Willmore-Integral

  

Dozent:

Prof. Dr. Ernst Kuwert

  

Zeit/Ort:

Mi, 14–16, SR 404 Eckerstr. 1

  

Übungen:

Achim Windel

  

Tutorium:

  

Web-Seite:

  

Inhalt:

Für eine zweidimensionale Fläche f : Σ → 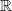ℝ3 ist das Willmore-Integral gegeben durch

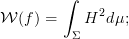
∫ W (f) = H2d μ; Σ
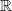dabei ist H die mittlere Krümmung und μ das induzierte Flächenmaß. Eine zentrale Eigenschaft des Funktionals ist die Invarianz unter der Gruppe der Möbiustransformationen des ℝn. Die zugehörige Euler Lagrange Gleichung ist ein quasilineares elliptisches System vierter Ordnung, die Lösungen heißen Willmoreflächen.

Die Vorlesung startet mit geometrischen Formeln und Grundlagen, sowie Ungleichungen von Willmore and Li-Yau. Der weitere Schwerpunkt soll auf analytischen Ergebnissen aus den letzten zehn Jahren liegen.

Typisches Semester:

7. Semester

Studienschwerpunkt:

Analysis, Differentialgeometrie

Notwendige Vorkenntnisse:

(Elementare) Differentialgeometrie

Nützliche Vorkenntnisse:

Partielle Differentialgleichungen

Sprechstunde Dozent:

Mi 11.15 – 12:15

[prev] [prev-tail] [front] [up]