5.8 Grenzwertsätze in zufälligen Graphen
Arbeitsgemeinschaft: | Grenzwertsätze in zufälligen Graphen |
| | |
Dozent: | Prof. Dr. Ludger Rüschendorf |
| | |
Zeit/Ort: | Do 11–13, SR 218, Eckerstr. 1 |
| | |
Tutorium: | Olaf Munsonius |
| | |
Vorbesprechung: | Di., 10.07.2007, 13:30 Uhr, Zi. 232, Eckerstr. 1 |
| | |
Web-Seite: | http://www.stochastik.uni-freiburg.de/ WS-0708 |
| | |
| |
Inhalt:
Zufällige kombinatorische Graphen, in denen mögliche Kanten zwischen Knoten mit gewissen
Wahrscheinlichkeiten auftreten, dienen dazu, komplexe Netzwerke zu modellieren und haben
eine Vielzahl von Anwendungen, wie z. B. in der Informatik (Computernetzwerke). Das wohl
einfachste Modell eines zufälligen Graphen wurde von Erd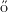 s und Rényi um 1960 eingeführt. In
diesem tritt jede mögliche Kante unabhängig von allen anderen mit fester Wahrscheinlichkeit p
auf.
s und Rényi um 1960 eingeführt. In
diesem tritt jede mögliche Kante unabhängig von allen anderen mit fester Wahrscheinlichkeit p
auf.
1999 konnte mit Hilfe von umfangreichen Statistiken gezeigt werden, dass das Modell von Erd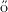 s und Rényi für die Beschreibung typischer realer Netzwerke ungeeignet ist, da es in der
Verteilung der Grade der einzelnen Knoten ein fundamental anderes Verhalten zeigt.
Seitdem wurde eine Vielzahl von zufälligen Graphmodellen entworfen, mit dem Ziel,
typische Eigenschaften realer Netzwerke, wie z. B. power-law-Verteilung der Grade, hohe
Clusterkoeffizienten oder small-world-Effekte wiederzugeben.
s und Rényi für die Beschreibung typischer realer Netzwerke ungeeignet ist, da es in der
Verteilung der Grade der einzelnen Knoten ein fundamental anderes Verhalten zeigt.
Seitdem wurde eine Vielzahl von zufälligen Graphmodellen entworfen, mit dem Ziel,
typische Eigenschaften realer Netzwerke, wie z. B. power-law-Verteilung der Grade, hohe
Clusterkoeffizienten oder small-world-Effekte wiederzugeben.
Typisches Semester: | 7. Semester |
Sprechstunde Dozent: | Di 11–12, Zi. 242, Eckerstr. 1 |
Sprechstunde Assistent: | Mi 10–11, Zi. 228, Eckerstr. 1 |
| |
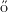 s und Rényi um 1960 eingeführt. In
diesem tritt jede mögliche Kante unabhängig von allen anderen mit fester Wahrscheinlichkeit p
auf.
s und Rényi um 1960 eingeführt. In
diesem tritt jede mögliche Kante unabhängig von allen anderen mit fester Wahrscheinlichkeit p
auf.