[prev] [prev-tail] [tail] [up]

Lehrveranstaltungen

 

1. Vorlesungen

PIC    

Abteilung für
Angewandte Mathematik
SS2016 PIC________________________________________________________

Vorlesung:  

Numerik (2. Teil der zweisemestrigen Veranstaltung)

  

Dozent:  

Prof. Dr. S. Bartels

  

Zeit/Ort:  

Mi 14–16 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-std. (14-tägl.) n.V.

  

Tutorium:  

Dipl.-Math. A. Papathanassopoulos

  

Web-Seite:  

http://aam.uni-freiburg.de/bartels

  
 
_______________________________________________________________

Inhalt:
Die Numerik ist eine Teildisziplin der Mathematik, die sich mit der praktischen Lösung mathematischer Aufgaben beschäftigt. Dabei werden Probleme in der Regel nicht exakt sondern approximativ gelöst. Typische Beispiele sind die Bestimmung von Nullstellen einer Funktion oder die Lösung linearer Gleichungssysteme. In der Vorlesung werden einige grundlegende numerische Algorithmen vorgestellt und im Hinblick auf Rechenaufwand sowie Genauigkeit untersucht. Die Vorlesung ist der zweite Teil eines zweisemestrigen Kurses. Der Besuch der begleitenden praktischen Übungen wird empfohlen. Diese finden 14-täglich im Wechsel mit der Übung zur Vorlesung statt.

Literatur:

1.)
S. Bartels : Numerik 3x9. Springer, 2016.
2.)
R. Plato : Numerische Mathematik kompakt. Vieweg, 2006.
3.)
R. Schaback, H. Wendland : Numerische Mathematik. Springer, 2004.
4.)
J. Stoer, R. Burlisch : Numerische Mathematik I, II. Springer, 2007, 2005.
5.)
G. Hämmerlin, K.-H. Hoffmann : Numerische Mathematik. Springer, 1990.
6.)
P. Deuflhard, A. Hohmann, F. Bornemann : Numerische Mathematik I, II. DeGruyter, 2003.
_

Typisches Semester:  

4. Semester

ECTS-Punkte:  

(für Teile 1 und 2 der Vorlesung zusammen) 9 Punkte

Notwendige Vorkenntnisse:  

Grundvorlesungen Lineare Algebra und Analysis

Studienleistung:  

Aktive Teilnahme an den Übungen

Prüfungsleistung:  

Klausur nach dem 2. Teil

Sprechstunde Dozent:  

Mi 12–13 Uhr, Zi. 209, Hermann-Herder-Str. 10, u. n.V.

Sprechstunde Assistent:  

Di 11–12 Uhr, Zi. 208, Hermann-Herder-Str. 10, u. n.V.

 
PIC
SS2016 PIC_________________________________________________________

Vorlesung:  

Stochastik (2. Teil der zweisemestrigen Veranstaltung)

  

Dozent:  

N. N.

  

Zeit/Ort:  

Di 14–16 Uhr, HS Rundbau, Albertstr. 21

  

Übungen:  

2-std. (14-tägl.), n. V.

  

Tutorium:  

Felix Hermann

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
 
Der zweite Teil der Stochastik behandelt allgemeine Wahrscheinlichkeitsräume, das starke Gesetz großer Zahlen und den zentralen Grenzwertsatz. Darüber hinaus wird einen Fortführung in Grundprobleme der Statistik gegeben, wie erwartungstreue Schätzer, Maximum-Likelihood-Schätzer und Testtheorie.

Literatur:

1.)
Czado, C. ; Schmidt, T. : Mathematische Statistik, Springer 2011
2.)
Dümbgen, L. : Stochastik für Informatiker, Springer 2003
3.)
Georgi, H.-O. : Stochastik, Walter de Gruyter 2002
4.)
Kersting, G. ; Wakolbinger, A. : Elementare Stochastik, Birkhäuser 2008
5.)
Krengel, U. : Einführung in die Wahrscheinlichkeitstheorie und Statistik, Vieweg 2005
__________

Typisches Semester:  

4. Semester

Notwendige Vorkenntnisse:  

Grundvorlesungen Lineare Algebra und Analysis

Folgeveranstaltungen:  

Wahrscheinlichkeitstheorie

Studienleistung:  

regelmäßige und erfolgreiche Teilnahme an den Übungen

Prüfungsleistung:  

Klausur am Ende des 2. Teils

Sprechstunde Dozent:  

n.V.

Sprechstunde Assistent:  

Di, Mi 10–12 Uhr, Zi. 244, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Elementargeometrie

  

Dozent:  

JProf. Dr. Nadine Große

  

Zeit/Ort:  

Fr 10–12 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-std. (14-tägl.) n.V.

  

Tutorium:  

Dr. Doris Hein

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/ngrosse/teaching/ElemGeo.html

  
 
_______________________________________________________________

Inhalt:
Geometrie ist ein wichtiger Bestandteil unseres täglichen Lebens ; sie hilft uns, uns im uns umgebenden Raum zurechtzufinden. Wir lernen die mathematischen Grundlagen der Euklidischen und nicht-Euklidischen Geometrie kennen und behandeln einige ausgewählte Themen :

Die Veranstaltung ist verpflichtend für Studierende des Lehramts nach der Prüfungsordnung von 2010, kann aber auch im Bachelor Mathematik besucht werden.

Literatur:

1.)
C. Bär, Elementare Differentialgeometrie, Walter de Gruyter, 2010.
2.)
C. Bär, Elementargeometrie, Vorlesungsskript, http://geometrie.math.uni-potsdam.de/index.php/de/lehre2/lehrmaterialien
3.)
M. Berger, Geometry I, Universitext, Springer-Verlag, 2009.
4.)
R. Hartshorne, Geometry : Euclid and beyond, Springer, 2000.
5.)
H. Knörrer, Geometrie, Vieweg, 1996.
________________________________________________________________________

Typisches Semester:  

ab 2. Semester

ECTS-Punkte:  

4 Punkte

Notwendige Vorkenntnisse:  

Analysis I

Sprechstunde Dozent:  

Mi 13 :10–13 :55 Uhr, Zi. 325, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 323, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Funktionentheorie

  

Dozentin:  

Prof. Dr. Annette Huber-Klawitter

  

Zeit/Ort:  

Mo, Mi 10–12 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-std.

  

Tutorium:  

Dr. Oliver Bräunling

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/arithgeom/lehre/ss16/ftheorie/ftheorie16.htm

  
 
_______________________________________________________________

Inhalt:
Die Funktionentheorie beschäftigt sich mit Funktionen f : ℂ →ℂ, die komplexe Zahlen auf komplexe Zahlen abbilden. Viele Konzepte der ANALYSIS I lassen sich direkt auf diesen Fall übertragen, z.B. die Definition der Differenzierbarkeit. Man würde vielleicht erwarten, dass sich dadurch eine zur ANALYSIS I analoge Theorie entwickelt, doch viel mehr ist wahr : Man erhält eine in vielerlei Hinsicht elegantere und einfachere Theorie. Beispielsweise impliziert die komplexe Differenzierbarkeit auf einer offenen Menge, dass eine Funktion sogar unendlich oft differenzierbar ist, und dies stimmt weiter mit Analytizität überein. Für reelle Funktionen sind alle diese Begriffe unterschiedlich. Doch auch einige neue Ideen sind notwendig : Für reelle Zahlen a,b integriert man für

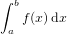
∫ b f(x)dx a

über die Elemente des Intervalls [a,b] bzw. [b,a]. Sind a,b jedoch komplexe Zahlen, ist nicht mehr so klar, wie man ein solches Integral auffassen soll. Man könnte z.B. in den komplexen Zahlen entlang der Strecke, die a,b ∈ℂ verbindet, integrieren, oder aber entlang einer anderen Kurve, die von a nach b führt. Führt dies zu einem wohldefinierten Integralbegriff oder hängt ein solches Kurvenintegral von der Wahl der Kurve ab ?

Literatur:

1.)
L. Ahlfors : Complex analysis
2.)
W. Fischer : Funktionentheorie
3.)
E. Freitag, R. Busam : Funktionentheorie
4.)
K. Jänich : Funktionentheorie
5.)
W. Rudin : Real and Complex Analysis
6.)
J.B. Conway : Functions of one complex variable
7.)
S. Lang : Complex analysis
_______________________________________________________________________________________

Typisches Semester:  

ab 4. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis I und Lineare Algebra I

Nützliche Vorkenntnisse:  

Analysis II

Studienleistung:  

erfolgreiche Teilnahme an Übungen ; siehe Modulhandbuch

Prüfungsleistung:  

siehe Modulhandbuch

Sprechstunde Dozentin:  

Di 10 :30–11 :30 Uhr, Zi. 434, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 436, Eckerstr. 1

 

Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Topologie

  

Dozent:  

Prof. Dr. V. Bangert

  

Zeit/Ort:  

Di, Do 12–14 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-std. n. V.

  

Tutorium:  

Dr. B. Mramor

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/geometrie/lehre/ss2016/vorlesung/Topologie/index.html

  
 
_______________________________________________________________

Inhalt:
Die Vorlesung baut auf den Kenntnissen auf, die in den Vorlesungen „Analysis I, II“ über die Topologie von ℝ und ℝn erworben wurden. Sie besteht aus zwei Teilen. Im ersten und längeren Teil wird die mengentheoretische Topologie bis zu dem Grad entwickelt, der für fortgeschrittene Vorlesungen in fast allen Bereichen der Mathematik nützlich ist. Der zweite Teil bietet eine Einführung in die Idee und in einige elementare Gegenstände der algebraischen Topologie (Homotopie, Fundamentalgruppe und Überlagerungen). Diese Begriffe spielen schon in den elementaren Teilen der Analysis, Funktionentheorie und Geometrie eine wichtige Rolle. Zur Vorlesung existiert ein Skriptum.

Literatur:

1.)
K. Jänich : Topologie, 8. Auflage 2005, Springer
2.)
B. von Querenburg : Mengentheoretische Topologie, 3. Auflage 2001, Springer
__________________

Typisches Semester:  

4.–6. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis I–II und Lineare Algebra I

Folgeveranstaltungen:  

Im WS 2016/17 ein Seminar für Studierende im Lehramtsstudiengang

Studienleistung:  

Erfolgreiche Bearbeitung von 50% der Übungsaufgaben

Prüfungsleistung:  

Studienleistung plus Klausur

Sprechstunde Dozent:  

Di 14–15 Uhr, Zi. 335, Eckerstr. 1

Sprechstunde Assistent:  

Mo 13–16 Uhr, Zi. 327, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Kommutative Algebra und Einführung in die algebraische Geometrie

  

Dozent:  

Prof. Dr. Stefan Kebekus

  

Zeit/Ort:  

Mi, Fr 8–10 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-std. n. V.

  

Tutorium:  

Dr. Hannah Bergner

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/kebekus/

  
 
_______________________________________________________________

Inhalt:
Kommutative Algebra ist eine allgemeinere Version der linearen Algebra über kommutativen Ringen statt über Körpern. Der Begriff des Moduls ersetzt den des Vektorraums. Weite Teile von Geometrie und Analysis verwenden diese Konzepte oder Variationen. Hauptanwendungsgebiet sind jedoch Zahlentheorie und algebraische Geometrie. Wir werden die formale Theorie daher mit einem der wichtigsten Anwendungsfälle kombinieren und gleichzeitig die Grundlagen der algebraischen Geometrie erarbeiten.

Algebraische Varietäten sind Lösungsmengen polynomialer Gleichungssysteme. Dies sind geometrische Objekte, die wir mit algebraischen Methoden studieren. Die Theorie der affinen Varietäten entspricht der Theorie der Ideale in Polynomringen mit endlich vielen Variablen. Damit ist der Bogen zur kommutativen Algebra gespannt.

Literatur:

1.)
Atiyah, MacDonald : Introduction to commutative algebra
2.)
Mumford : The red book of varieties and schemes
3.)
Shafarevich : Basic algebraic geometry
4.)
Eisenbud : Commutative Algebra with a View Toward Algebraic Geometry
5.)
Fulton : Algebraic Curves,  http://www.math.lsa.umich.edu/wfulton/CurveBook.pdf
___

Typisches Semester:  

ab dem 4. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Lineare Algebra

Nützliche Vorkenntnisse:  

Algebra

Folgeveranstaltungen:  

wird im WS 16/17 angeboten

Studienleistung:  

Übungsaufgaben

Prüfungsleistung:  

Klausur

Sprechstunde Dozent:  

Mi 13–14 Uhr, Zi. 432, Eckerstr. 1

Sprechstunde Assistentin:  

Di 14–17 Uhr, Zi. 422, Eckerstr. 1

 
PIC      
Abteilung für
Mathematische Logik
SS2016 PIC_________________________________________________________

Vorlesung:  

Mathematische Logik

  

Dozentin:  

Heike Mildenberger

  

Zeit/Ort:  

Di, Do 10–12 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2std. n.V.

  

Tutorium:  

Fiorella Guichardaz

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/mildenberger/veranstaltungen/ss16/MathLogik.html

  
 
_______________________________________________________________

Inhalt:
Dies ist eine Einführung in die mathematische Logik. Der Begriff eines mathematischen Beweises wird präzisiert. Kann man das Nachprüfen von Beweisen oder gar das Finden von Beweisen geeigneten Computern überlassen ? Von welchen (nicht beweisbaren) Grundprinzipien geht man aus ? Gegenstände der Vorlesung sind der Gödel’sche Vollständigkeitssatz und die Gödel’schen Unvollständigkeitssätze und Einführungen in die ersten Grundlagen der Rekursionstheorie, der Modelltheorie und der Mengenlehre.

Information über die Studien- und die Prüfungsleistung findet man auf der Webseite der Vorlesung.

Literatur:

1.)
H.-D. Ebbinghaus, J. Flum, W. Thomas, Einführung in die mathematische Logik, Spektrum Verlag, 2007.
2.)
Mildenberger, Skript „Mathematische Logik”.
3.)
Joseph R. Shoenfield, Joseph, Mathematical logic. Reprint of the 1973 second printing. Association for Symbolic Logic, Urbana, IL ; A K Peters, Ltd., Natick, MA, 2001.
4.)
Ziegler, Skript „Mathematische Logik”.
5.)
Martin Ziegler, Mathematische Logik, Birkhäuser, 2010.
_________________________________________________

Typisches Semester:  

ab dem vierten Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Anfängervorlesungen

Folgeveranstaltungen:  

weiterführende Vorlesungen in der mathematischen Logik

Sprechstunde Dozentin:  

Di 13–14 Uhr, Zi. 310, Eckerstr. 1

Sprechstunde Assistentin:  

n.V., Zi. 307, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Funktionalanalysis

  

Dozent:  

Prof. Dr. Patrick Dondl

  

Zeit/Ort:  

Mo, Mi 12–14 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Übungen:  

2-std. n. V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http://aam.uni-freiburg.de/abtlg/ls/lsdo/lv/fa_ss16

  
 
_______________________________________________________________

Inhalt:
In der Funktionalanalysis betrachten wir die Eigenschaften unendlichdimensionaler Vektorräume und der Abbildungen zwischen solchen Räumen. Insbesondere liegt in dieser Vorlesung das Augenmerk auf Funktionenräumen und Abbildungen, die bei der Lösung von partiellen Differentialgleichungen eine Rolle spielen : Im Gegensatz zum klassischen Zugang, bei dem eine Differentialgleichung als punktweise Bedingung an eine Funktion aufgefasst wird, interpretieren wir im funktionalanalytischen Zugang den Differentialoperator als lineare Abbildung zwischen zwei geeigneten Funktionenräumen. Die Frage nach der Wohlgestelltheit der Differentialgleichung ist dann gleichbedeutend mit der Frage, ob diese lineare Abbildung bijektiv ist und die inverse Abbildung stetig ist.

Im Vergleich zur linearen Algebra treten bei der Behandlung unendlichdimensionaler Räume neue Probleme auf – zum Beispiel ist nicht mehr jede lineare Abbildung automatisch stetig und nicht jede beschränkte Folge besitzt eine konvergente Teilfolge. Wir beweisen in der Vorlesung eine Reihe von Sätzen, die helfen solche Schwierigkeiten zu überwinden. Beispielsweise führen wir eine neue Art von Konvergenz (die sogenannte „schwache Konvergenz“) ein, für welche solche konvergenten Teilfolgen beschränkter Folgen in geeigneten Funktionenräumen wieder existieren.

Literatur:

1.)
H. Brézis : Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer 2011
2.)
H.W. Alt : Lineare Funktionalanalysis. Springer 2012
3.)
M. Dobrowolski : Angewandte Funktionalanalysis. Springer 2010
_____________________________________

Typisches Semester:  

4. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis I–III, Lineare Algebra I–II

Prüfungsleistung:  

Klausur

Sprechstunde Dozent:  

Wird in der Vorlesung bekannt gegeben

Sprechstunde Assistent:  

Wird in der Vorlesung bekannt gegeben

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Partielle Differentialgleichungen

  

Dozent:  

Prof. Dr. Guofang Wang

  

Zeit/Ort:  

Mo, Mi 14–16 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-std. n. V.

  

Tutorium:  

Z. Sun

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/home/Wang

  
 
_______________________________________________________________

Inhalt:

In dieser Vorlesung untersuchen wir die linearen elliptischen partiellen Differentialgleichungen.

∙ die harmonische Funktionen

∙ die Poisson-Gleichungen

∙ das Maximum-Prinzip

∙ die Schauder-Theorie

∙ die Krylov-Safonov-Theorie

∙ die Moser-Theorie

Literatur:

1.)
Evans, Lawrence C. : Partial differential equations, Graduate Studies in Mathematics. 19, Providence, RI : American Mathematical Society (AMS) (1998)
2.)
Han, Qing : An Introduction to Elliptic Differential Equations, manuscript
3.)
Jost, Jürgen : Partielle Differentialgleichungen, Springer (1998)
__________________________________________________________________________________________________________________________

Typisches Semester:  

ab dem 5. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Analysis III

Nützliche Vorkenntnisse:  

Funktionalanalysis

Folgeveranstaltungen:  

PDE II oder Seminar

Sprechstunde Dozent:  

Mi 11 :15-12 :15 Uhr, Zi. 209, Eckerstr. 1

Sprechstunde Assistent:  

Di 14–16 Uhr, Zi. 204, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Algebraische Zahlentheorie

  

Dozent:  

Dr. Fritz Hörmann

  

Zeit/Ort:  

Di, Do 14–16 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-std. n. V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/arithgeom/lehre/ss16/algzt.html

  
 
_______________________________________________________________

Inhalt:
Zahlentheorie beschäftigt sich mit den Eigenschaften der ganzen Zahlen. Fragen nach der Lösbarkeit von Gleichungen (z.B. x3 + y3 = z3) führen schnell dazu, dass man den Zahlbereich vergrößert (z.B. x3 + y3 = (x + y)(x + ρy)(x + ρ2y) für ρ = e2πi?3). Algebraische Zahlentheorie konzentriert sich auf diese Verallgemeinerungen von ℤ und ihre Eigenschaften.

Wir wollen diese Zahlbereiche definieren und ihre grundlegenden Eigenschaften studieren. Sie verhalten sich zum Teil ähnlich zu den ganzen Zahlen, aber es treten auch neue Phänomene auf. Betrachtet man zum Beispiel den Zahlbereich

ℤ[√ --5] = {x + y√ --5 | x,y ∈ ℤ },

so gibt es keine eindeutige Primfaktorzerlegung mehr, wie man an den beiden wesentlich verschiedenen Zerlegungen

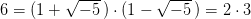
√ --- √ --- 6 = (1 + - 5 ) ⋅ (1 - - 5) = 2 ⋅ 3

sehen kann. Wichtigste Ziele sind die Endlichkeit der Klassenzahl (sie misst, wie sehr die Eindeutigkeit der Primfaktorzerlegung fehlschlägt) und der Dirichletsche Einheitensatz.

Literatur:

1.)
J. Neukirch, Algebraische Zahlentheorie
2.)
S. Lang, Algebraic Number Theory
3.)
P. Samuel, Algebraic Theory of Numbers
4.)
A. Weil, Basic Number Theory
_______________________________________________________________________________

Typisches Semester:  

ab 5. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Algebra und Zahlentheorie

Nützliche Vorkenntnisse:  

Kommutative Algebra

Studienleistung:  

Lösen von Übungsaufgaben und Teilnahme an den Übungen

Prüfungsleistung:  

Klausur

Sprechstunde Dozent:  

Di 16–18 Uhr, Zi. 421, Eckerstr. 1

Kommentar:  

Diese Veranstaltung wird nur in größeren Abständen angeboten.

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Ausgewählte Gegenstände der Darstellungstheorie

  

Dozent:  

Prof. Dr. W. Soergel

  

Zeit/Ort:  

Di, Do 8–10 Uhr, SR 404, Eckerstr. 1

  

Übungen:  

2-std. n. V.

  

Tutorium:  

Dr. A. Sartori

  
 
_______________________________________________________________

Inhalt:
Das zentrale Thema der Vorlesung im Sommersemester soll die Kategorie 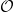O von Bernstein-Gelfand-Gelfand werden, die einen besonders gut zugänglichen Modellfall für allgemeinere Kategorien von Darstellungen bildet. Wie ausführlich die Motivation zur Untersuchung dieser Kategorie von Darstellungen und Grundlagen zu halbeinfachen Lie-Algebren diskutiert werden, wird von den Hörern abhängen.

Literatur:

1.)
Humphreys, Representations of Semisimple Lie Algebras in the BGG-category O, AMS 2008
__________________________________________________________________________________________________________________________

Typisches Semester:  

6. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

Grundvorlesungen, Algebra und Zahlentheorie, Einführung in die kommutative Algebra und algebraische Geometrie

Sprechstunde Dozent:  

Mi 12 :30–13 :30 Uhr, Zi. 429, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 419, Ecerkstr. 1

 
PIC      
Abteilung für
Mathematische Logik
SS2016 PIC_________________________________________________________

Vorlesung:  

Ausgewählte Gegenstände der Modelltheorie

  

Dozent:  

Martin Ziegler

  

Zeit/Ort:  

Di, Mi 12–14 Uhr, SR 404. Eckerstr. 1

  

Übungen:  

2-std.

  

Tutorium:  

Juan-Diego Caycedo

  

Web-Seite:  

http ://home.mathematik.uni-freiburg.de/ziegler/ veranstaltungen/ss16-modelltheorie.html

  
 
_______________________________________________________________

Inhalt:
Die Vorlesung kann als Supplement zum unten angegebenen Lehrbuch dienen. Es gibt sechs Kapitel.

1.
Zellzerlegungssatz in o-minimalen Theorien.
2.
Modelltheorie henselscher bewerteter Körper.
3.
ACFA, die Theorie algebraisch abgeschlossener Körper mit generischem Automorphismus.
4.
Continuous Logic, die Modelltheorie metrischer Strukturen.
5.
Hrushovskis Satz über die Gruppenkonfiguration.
6.
Modelltheorie von Moduln.

Literatur:

1.)
K. Tent, M.Ziegler Introduction to Model Theory
______________________________________________________

Typisches Semester:  

6. Semester

ECTS-Punkte:  

9 Punkte

Nützliche Vorkenntnisse:  

Modelltheorie I oder Mathematische Logik

Sprechstunde Dozent:  

n.V., Zi. 313, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 304, Eckerstr. 1

 
PIC
SS2016 PIC_________________________________________________________

Vorlesung:  

Stochastische Integration und Finanzmathematik
  

Dozent:  

Prof. Dr. Thorsten Schmidt

  

Zeit/Ort:  

Di, Mi 10–12 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-std. n. V.

  

Tutorium:  

Wahid Khosrawi-Sardroudi

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/schmidt

  
 
_______________________________________________________________

Inhalt:
Im Anschluss an die Vorlesung stochastische Prozesse befasst sich diese Vorlesung nun ausführlich mit den Finanzmathematischen Fragestellungen. Zunächst wird, ganz ohne stochastisches Kalkül Finanzmathematik in diskreter Zeit bearbeitet werden. Hier können viele Fragestellung bereits ausführlich behandelt werden. Anschließend werden die allgemeinen Fundamentalsätze für Semimartingale abgeleitet. Es schließt sich die Behandlung von Zins- und Kreditrisikomärkten an und die Anwendung auf affine Zinsstrukturmodelle.

Literatur:

1.)
Föllmer/Schied : Stochastic Finance
2.)
Delbaen/Schachermayer : The Mathematics of Arbitrage
3.)
Filipovic : Term Structure Models
______________________________________________________________________________

Typisches Semester:  

ab dem 2. Semester im Master

ECTS-Punkte:  

9 Punkte

Sprechstunde Dozent:  

n.V., Zi. 247, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 224, Eckerstr. 1

 

PIC    

Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Modellierung

  

Dozent:  

Prof. Dr. M. Růžička

  

Zeit/Ort:  

Do 10–12 Uhr, SR 404, Eckerstr. 1

  

Übungen:  

2-std. n. V.

  

Tutorium:  

H. Eberlein

  

Web-Seite:  

http://aam.uni-freiburg.de/lehre/ss16/modellierung

  
 
_______________________________________________________________

Inhalt:
Als Modelle für viele physikalische Vorgänge, wie z. B. der Bestimmung einer Temperaturverteilung, der Beschreibung von Schwingungen von Membranen oder von Strömungen von Flüssigkeiten, treten partielle Differentialgleichungen auf.

Im ersten Teil der Vorlesung werden wir diese Grundgleichungen der Mathematischen Physik aus der Sicht der Kontinuumsmechanik herleiten sowie Grundprinzipien für die Modellierung von Materialeigenschaften kennenlernen.

Im zweiten Teil der Vorlesung werden wir die mathematische Theorie der stationären Stokesgleichungen entwickeln.

Literatur:

1.)
Chadwick,Continuum Mechanics, Dover, (1999).
2.)
Girault, Raviart, Finite Element Methods for Navier–Stokes Equations, Springer, (1986).
___

Typisches Semester:  

ab 6. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Einführung in Theorie und Numerik Partieller Differentialgleichungen oder Funktionalanlysis

Sprechstunde Dozent:  

Mi 13–14 Uhr, Zi. 145, Eckerstr. 1

Sprechstunde Assistent:  

Do 14–17 Uhr, Zi. 144, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Symplektische Geometrie

  

Dozent:  

Dr. Doris Hein

  

Zeit/Ort:  

Di 14–16 Uhr, SR 404, Eckerstr. 1

  

Übungen:  

2-std. n. V.

  

Tutorium:  

N. N.

  
 
_______________________________________________________________

Inhalt:
Symplektische Geometrie ist die natürliche Geometrie, die Hamiltonschen Systemen und damit einer Formulierung der klassischen Mechanik zugrunde liegt.

In dieser Vorlesung werden wir zunächst lineare symplektische Geometrie anschauen, die statt eines Skalarproduktes eine schiefsymmetrische Bilinearform zugrunde legt und nur in geraden Dimensionen existiert. Danach werden die Begriffe dann auf Mannigfaltigkeiten verallgemeinert, indem wir uns Differentialformen anschauen und die Eigenschaften einer symplektischen Form in diese Sprache übersetzen. Hierbei stellt sich heraus, dass lokal alle symplektischen Mannigfaltigkeiten gleich aussehen.

Außerdem werden wir symplektische Abbildungen und insbesondere Hamiltonsche Systeme und ihre Eigenschaften beschreiben. Insbesondere gibt es in der Sprache der symplektischen Geometrie einfache Formulierungen für physikalische Aussagen wie Energieerhaltung. Falls Zeit bleibt, leiten wir daraus die Kontaktgeometrie her, die ungerade Dimensionen betrachtet und der symplektischen Geometrie sehr ähnlich ist.

Literatur:

1.)
Eduard Zehnder, Lectures on Dynamical Systems, EMS Textbooks in Mathematics. European Mathematical Society (EMS), Zürich
2.)
Cannas da Silva, Lectures on symplectic geometry, Lecture Notes in Mathematics, 1764. Springer-Verlag, Berlin, 2001
3.)
McDuff, Dusa, Salamon, Dietmar, Introduction to symplectic topology. Second edition. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York, 1998
_

Typisches Semester:  

ab 6. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Analysis, Lineare Algebra, Differentialgeometrie

Sprechstunde Dozent:  

n.V., Zi. 323, Eckerstr. 1

 
PIC
SS2016 PIC_________________________________________________________

Vorlesung:  

Markovketten

  

Dozent:  

Dr. Andrej Depperschmidt

  

Zeit/Ort:  

Mo 8–10 Uhr, SR 404, Eckerstr. 1

  

Übungen:  

2-std. n. V. in der ersten Vorlesung

  

Tutorium:  

Benedikt Köpfer

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
Markovprozesse ist eine für viele Anwendungen wichtige Klasse von stochastischen Prozessen. In dieser Vorlesung beschäftigen wir uns hauptsächlich mit einer speziellen Unterklasse von Markovprozessen, nämlich Markovketten in diskreter Zeit. Einfache Irrfahrt auf den ganzen Zahlen ist eins der wichtigen Beispiele. Eine Auswahl aus der Fülle von weiteren wichtigen Beispielen wird sowohl in der Vorlesung als auch in den Übungen behandelt. Es werden grundlegende Begriffe wie Irreduzibilität, Aperiodizität, Rekurrenz, Transienz erläutert und das Langzeitverhalten von Markovketten studiert. Mit dem Ergodensatz werden wir eine Verallgemeinerung der Gesetze der großen Zahlen auf Markovketten kennenlernen.

Literatur:

1.)
P. Brémaud, Markov chains. Gibbs fields, Monte Carlo simulation, and queues., Springer, 1999.
2.)
O. Häggström, Finite Markov chains and algorithmic applications, Cambridge University Press, 2002.
3.)
A. Klenke, Wahrscheinlichkeitstheorie., 2nd edn, Springer, 2008.
4.)
J. Norris, Markov chains., Cambridge University Press, 1997.
_________________________________________

Typisches Semester:  

6. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Stochastik

Nützliche Vorkenntnisse:  

Wahrscheinlichkeitstheorie

Sprechstunde Dozent:  

Do 12–13 Uhr, Zi. 248, Eckerstr. 1

Sprechstunde Assistent:  

Mi 14–16 Uhr, Do 9–11 Uhr, Zi. 227, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Numerik für Differentialgleichungen

  

Dozent:  

Prof. Dr. Patrick Dondl

  

Zeit/Ort:  

Mo 16–18 Uhr, HS II, Albertstr. 23b

  

Übungen:  

2-std. n. V. (14-tägl.)

  

Tutorium:  

N. N.

  

Web-Seite:  

http://aam.uni-freiburg.de/abtlg/ls/lsdo/lv/numdgl_ss16

  
 
_______________________________________________________________

Inhalt:
Differentialgleichungen sind ein wichtiges mathematisches Werkzeug zur Beschreibung realer Vorgänge wie beispielsweise der Flugbahn eines Körpers. In der Vorlesung werden numerische Verfahren zur praktischen Lösung gewöhnicher Differentialgleichungen der Form y′(t) = f(t,y(t)) sowie einfacher partieller Differentialgleichungen, bei denen mehrere unabhängige Variablen auftreten, diskutiert.

Literatur:

1.)
R. Plato : Numerische Mathematik kompakt. Vieweg 2006
2.)
R. Schaback, H. Wendland : Numerische Mathematik. Springer 2004.
3.)
J. Stoer, R. Bulirsch : Numerische Mathematik I, II. Springer 2007, 2005.
4.)
W. Walter : Gewöhnliche Differentialgleichungen : Eine Einführung. Springer 2000.
5.)
M. Hanke-Bourgeois : Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Vieweg+Teubner 2006.
_____________________________________________________________________________

Typisches Semester:  

4. Semester

ECTS-Punkte:  

5 Punkte oder zusammen mit den Prakt. Übungen Numerik für Differentialgleichungen 6 Punkte

Notwendige Vorkenntnisse:  

Numerik I

Studienleistung:  

Aktive Teilnahme an den Übungen

Prüfungsleistung:  

Klausur

Sprechstunde Dozent:  

Wird in der Vorlesung bekannt gegeben

Sprechstunde Assistent:  

Wird in der Vorlesung bekannt gegeben

 
Abteilung für
Quantitative Finanzmarktforschung
SS2016 PIC_________________________________________________________

Vorlesung:  

Futures and Options

  

Dozent:  

Dr. E.A. v. Hammerstein

  

Zeit/Ort:  

Mo 14–16 Uhr, HS 1098, KG I

  

Übungen:  

Di 16–18 Uhr, HS 1, Alte Universität

  

Tutorium:  

Dr. E.A. v. Hammerstein

  

Web-Seite:  

http://www.finance.uni-freiburg.de

  
 
_______________________________________________________________

Inhalt:
This course covers an introduction to financial markets and products. Besides futures and standard put and call options of European and American type we also discuss interest-rate sensitive instruments such as swaps.
For the valuation of financial derivatives we first introduce financial models in discrete time as the Cox–Ross–Rubinstein model and explain basic principles of risk-neutral valuation. Finally, we will discuss the famous Black–Scholes model which represents a continuous time model for option pricing.

The course, which is taught in English, is offered for the first year in the Finance profile of the M.Sc. Economics program as well as for students of M.Sc. and B.Sc. Mathematics and M.Sc. Volkswirtschaftslehre.

For students who are currently in the B.Sc. Mathematics program, but plan to continue with the special profile “Finanzmathematik” within the M.Sc. Mathematics, it is recommended to credit this course for the latter profile and not for B.Sc. Mathematics.

Literatur:

1.)
Chance, D.M., Brooks, R. : An Introduction to Derivatives and Risk Management, 8th ed., South-Western, 2009
2.)
Hull, J.C. : Options, Futures, and other Derivatives, 7th ed., Prentice Hall, 2009
3.)
Shreve, S.E. : Stochastic Calculus for Finance I : The Binomial Asset Pricing Model, Springer Finance, 2005
4.)
Strong, R.A. : Derivatives. An Introduction, 2nd ed., South-Western, 2004
_______________________

Typisches Semester:  

ab 6. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Vorlesung Stochastik

Studienleistung:  

unbenotete Klausur (M.Sc. Mathematik)

Prüfungsleistung:  

Klausur (B.Sc. Mathematik)

Kommentar:  

Zulassungsvoraussetzung für die Abschlussklausur ist eine erfolgreiche Teilnahme an den Übungen

Sprechstunde Dozent:  

n.V., Zi. 01010, Alte Universität, Bertholdstraße 17

 
PIC
SS2016 PIC_________________________________________________________

Vorlesung:  

Stochastic Filtering

  

Dozent:  

N. N.

  

Zeit/Ort:  

Do 10–12 Uhr, HS II, Albertstr. 23 b

  

Übungen:  

2-std. n. V.

  

Tutorium:  

N. N.

  

Web-Seite:  

http ://www.stochastik.uni-freiburg.de

  
 
_______________________________________________________________

Inhalt:
Filtering is the task of recovering unobserved state variables from noisy observations. This course covers the theoretical foundations of filtering in various levels of generality, as well as numerics and applications. Topics covered in the course :

Literatur:

1.)
O. Cappé, E. Moulines, T. Ryden (2005). Inference in Hidden Markov Models. New York : Springer.
2.)
A. Bain and D. Crisan (2009). Fundamentals of Stochastic Filtering. New York : Springer.
____

Typisches Semester:  

2. Semester im Master-Studiengang

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Lecture : Stochastic Processes

Prüfungsleistung:  

Oral exam (20 minutes). For admission to the exam, solving 60% of the exercises and presenting at least once during the exercise class is required.

Sprechstunde Dozent:  

By arrangement

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Topologische Methoden in der Variationsrechnung
  

Dozent:  

Armin Schikorra

  

Zeit/Ort:  

Di 10–12 Uhr, SR 125, Eckerstr. 1

  

Übungen:  

2-std. n. V.

  

Tutorium:  

N. N.

  
 
_______________________________________________________________

Inhalt:

Wir betrachen geometrische Probleme, welche durch ein Zusammenspiel von Techniken der Variationsrechnung und topologischen Betrachtungen behandelt werden können.

Als erstes Ziel werden wir uns die Existenz von geschlossenen Geodäten auf Sphären-ähnlichen Mannigfaltigkeiten anschauen. Hierzu betrachten wir Homotopiegruppen der Mannigfaltigkeit und das sogenannte Min-max-Prinzip.

Literatur:

1.)
Kapitel 2 von M. Struwe, Variational Methods. Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 4th edition. Springer-Verlag, Berlin, 2008.
2.)
W. Klingenberg, Riemannian Geometry, 2nd version, De Gruyter-Verlag, Berlin, 1995.
________

Typisches Semester:  

6. und 8. Semester

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Analysis 3

Nützliche Vorkenntnisse:  

Variationsrechnung

Sprechstunde Dozent:  

Di 15–16 Uhr, Zi. 213, Eckerstr. 1

 

 

2. Berufsorientierte Veranstaltungen

Mathematisches Institut
SS2016 PIC_________________________________________________________

Veranstaltung:  

Lernen durch Lehren

  

Dozent:  

Alle Dozentinnen und Dozenten von Vorlesungen

  
 
_______________________________________________________________

Inhalt:
Bei diesem Modul handelt es sich um eine Begleitveranstaltung zu Tutoraten zu Mathematikvorlesungen. Teilnehmen können an dem Modul alle Studierenden in einem Bachelor- oder Master-Studiengang in Mathematik (einschließlich Zwei-Hauptfächer-Bachelor mit Mathematik als einem der beiden Fächer), die sich für das gleiche Semester erfolgreich um eine Tutoratsstelle zu einer Mathematikvorlesung beworben haben (mindestens eine zweistündige oder zwei einstündige Übungsgruppen über das ganze Semester, aber ohne Einschränkungen an die Vorlesung). Das Modul kann einmal im Bachelor-Studium und bis zu zweimal im Master-Studium absolviert werden und wird jeweils mit 3 ECTS-Punkten im Wahlmodulbereich (im Zwei-Hauptfächer-Bachelor : „Optionsbereich“) angerechnet. Es handelt sich um eine Studienleistung, d.h. das Modul wird nicht benotet.

Leistungsnachweis :

In Ermangelung eines passenden Wahlbereichs kann das Modul für Lehramtsstudierende in dieser Form zur Zeit nicht angeboten werden.__________________________________________________________

Typisches Semester:  

ab 5. Fachsemester

Kommentar:  

nur für Bachelor oder Master-Studiengang Mathematik ; Tutorat zu einer Mathematik-Vorlesung im gleichen Semester ist notwendige Voraussetzung

ECTS-Punkte:  

3 Punkte

Studienleistung:  

siehe Text oben
 

Abteilung für
Didaktik der Mathematik
SS2016 PIC_________________________________________________________

Vorlesung:  

Didaktik der Geometrie und Stochastik

  

Dozent:  

Martin Kramer

  

Zeit/Ort:  

2-std. zur Wahl : Mo 14–16 Uhr o. Di 10–12 Uhr o. Mi 10–12 Uhr, SR 404, Eckerstr. 1

  

Übungen:  

Alle Übungen finden kompakt in vier Treffen statt. Alle Zeiten sind Mo 10–12 Uhr, Di 16–18 Uhr und zu anderen Terminen Di 17–19 Uhr, SR 127, Eckerstr. 1

  

Teilnehmerliste:  

Bitte tragen Sie Ihren Wunschtermin im Campus-Management für die Vorlesung UND für das Tutorat ein.
Die Teilnehmerzahl sollte die Zahl 35 nicht übersteigen.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Die Vorlesungen über Didaktik bestehen aus zwei Teilen : Didaktik der Algebra und Analysis (WS) und Didaktik der Geometrie und Stochastik (SS).

Eine scharfe Abgrenzung der Einzelthemen ist im schulischen Kontext wenig hilfreich. So wird z.B. die Projektion auf den ersten Blick der Geometrie zugeordnet, andererseits entsteht durch die Projektion einer Drehbewegung die Sinus- bzw. Kosinusfunktion. Im Sinne einer ganzheitlichen und vernetzenden Didaktik werden in der Vorlesung viele Bezüge zwischen den einzelnen, innermathematischen Disziplinen geschaffen.

Erörtert werden didaktische Methoden der Geometrie und Stochastik, die didaktische Bedeutung des Materials im schulischen Kontext sowie die Bedeutung von kooperativem Lernen (Gruppenarbeit). Zentral ist der Wechsel zwischen symbolischen, ikonischen und enaktiven Repräsentationsebenen (nach Bruner). An konkreten Beispielen wird ein konstruktivistischer Vermittlungsansatz im Kontext der bildungsplanspezifischen Inhalte (lernen, begründen, problemlösen und kommunizieren) aufgezeigt.
Die Vorlesung legt Wert darauf, dass die dargestellte Didaktik konkret und interaktiv erlebt wird. Die Folge ist ein ständiger Rollenwechsel des Hörers : Einerseits erlebt er die Dinge aus der Schülerperspektive, auf der anderen Seite schlüpft er in die Rolle des reflektierenden Lehrers.

Literatur:

1.)
Bauer, J. : Warum ich fühle, was Du fühlst ; Hoffmann und Campe
2.)
Eichler A. ; Vogel M. : Leitidee Daten und Zufall : Von konkreten Beispielen zur Didaktik der Stochastik ; Wiesbaden : Vieweg + Teubner, 2009
3.)
Henn, J. : Geometrie und Algebra im Wechselspiel : Mathematische Theorie für schulische Fragestellungen ; Springer Spektrum, 2012
4.)
Kramer, M. : Mathematik als Abenteuer ; Aulis Verlag
5.)
Kramer, M. : Schule ist Theater ; Schneider-Verlag Hohengehren
6.)
Spitzer, M. : Geist im Netz – Modelle für Lernen, Denken und Handeln ; Spektrum Akademischer Verlag, Heidelberg
7.)
Thun, S. v. : Miteinander Reden, Bd. I–III ; Rowohlt Tb.
_________________________________

Typisches Semester:  

6. Semester

ECTS-Punkte:  

3 Punkte

Sprechstunde Dozent:  

n.V., Zi. 131, Eckerstr. 1

Kommentar:  

Bitte tragen Sie Ihren Wunschtermin im Campus-Management für die Vorlesung UND für das Tutorat ein.
Die Teilnehmerzahl sollte die Zahl 35 nicht übersteigen.

 
Abteilung für
Didaktik der Mathematik
SS2016 PIC_________________________________________________________

Fachdidaktikseminar:  

Mathematik jenseits des Klassenzimmers

  

Dozent:  

Martin Kramer

  

Zeit/Ort:  

4 Termine in Freiburg : 26.04., 03.05., 31.05., 21.06.,
Di 14 :00–17 :00 Uhr, SR 125, Eckerstr. 1 ;
Kompaktphase : 04.–09.09.2016 im Schwarzhornhaus bei Waldstetten (http://www.schwarzhornhaus.de/)

  

Vorbesprechung:  

Di 02.02.2016, 10 Uhr, Didaktik-Vorraum, Eckerstr. 1

  

Teilnehmerliste:  

Interessenten sollen sich bitte in eine bei Frau Schuler ausliegende Liste eintragen, Zi. 132, Di–Do, 9–13 Uhr und 14–16 :30 Uhr.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Ein Unterricht außerhalb des Klassenzimmers. Sei es auf dem Pausenhof, auf der Wiese vor der Schule, im Wald, in einem Mathe-Camp oder im Schullandheim. In Kleingruppen werden Lernumgebungen bzw. Erlebnisräume jenseits des Klassenzimmers entworfen und durchgeführt.

Konkrete Inhalte :

1.
Handlungs- und erlebnisorientierte Didaktik, konstruktivistische und subjektive Didaktik
2.
Rollenverständnis (Rollen des Lehrers, Wechsel von Rollen, Rollenbelegung von mathematischen Inhalten)
3.
Gruppendynamik (Gruppenentwicklungsphasen)
4.
Gruppenarbeit, innere Struktur von Gruppen für das Fach Mathematik (Farbgruppen, Rollenverständnis)
5.
Kommunikation (Quadratische Nachrichten, inneres Team, Umgang mit mathematisch belasteten Schülern)
6.
Konkretes Erleben verschiedener Lernumgebungen (z.B. Schatzsuche mit Vektoren, Thaleskreis, Spielkasino, Brückenbau mit Erbsen und Zahnstochern, …)
7.
Studenten entwerfen eigene Erlebnisräume, die anschließend durchspielt werden.
8.
Mathematisierung eines Klettergartens.

Zur Unterkunft : Das Schwarzhornhaus bei Waldstetten (http://www.schwarzhornhaus.de/) ist ein Selbstversorgerhaus. Es wird gemeinsam gekocht. Übernachtet wird in Mehrbettzimmern (Schullandheim). Eigenen Bettbezug bitte mitbringen.

Kosten und Teilnehmerzahl : Die Eigenbeteiligung pro Person beträgt max. 65 Euro. Maximal 12 Teilnehmer._____________________________________________________________________________________

Typisches Semester:  

nach dem Praxissemester

ECTS-Punkte:  

4 Punkte

Prüfungsleistung:  

Klausur am 28.06.2016, 14 :00–17 :00 Uhr, SR 125, Eckerstr. 1

Sprechstunde Dozent:  

n.V., Zi. 131, Eckerstr. 1

 
Abteilung für
Didaktik der Mathematik
SS2016 PIC_________________________________________________________

Fachdidaktikseminar:  

Mathematik in der Unterstufe
– Grundlagen, Inhalte und Didaktik

  

Dozent:  

Holger Dietz

  

Zeit/Ort:  

Do 10–13 Uhr, SR 127, Eckerstr. 1

  

Vorbesprechung:  

Do 14.04.2016, 14 :00 Uhr, Didaktik-Vorraum, Eckerstr. 1

  

Teilnehmerliste:  

Interessenten sollen sich bitte in eine bei Frau Schuler ausliegende Liste eintragen, Raum 132, Di–Do, 9–13 Uhr und 14–16 :30 Uhr.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Mathematik(unterricht) in der Schule unterscheidet sich notwendigerweise inhaltlich und methodisch-didaktisch grundlegend von dem, was man aus universitären Vorlesungen, aber auch aus der Kursstufe kennt. Diese Veranstaltung widmet sich den Besonderheiten, Möglichkeiten und Herausforderungen, die mit dem Unterrichten von Mathematik in der Schule, insbesondere in der Unterstufe, einhergehen. Exemplarische Themengebiete und Unterrichtsinhalte werden hinsichtlich ihrer Relevanz für die Lebenswelt der Kinder, die Schulmathematik und Wissenschaft analysiert aber auch didaktisch und methodisch anhand gängiger bzw. selbst konzipierter Umsetzungsbeispiele in den Unterricht eingebettet.__________________________________

Typisches Semester:  

ab 3. Semester

ECTS-Punkte:  

4 Punkte

Nützliche Vorkenntnisse:  

Anfängervorlesungen

Sprechstunde Dozent:  

n.V.

 
Abteilung für
Didaktik der Mathematik
SS2016 PIC_________________________________________________________

Fachdidaktikseminar:  

Digitale Mathematikwerkzeuge im Unterricht

  

Dozent:  

Clemens Baur

  

Zeit/Ort:  

Do 14–16 Uhr, SR 125, Eckerstr. 1

  

Übungen:  

Do 16–17 Uhr, SR 125, Eckerstr. 1

  

Vorbesprechung:  

Di, 12.04.2016, 14 :00 Uhr in der Didaktik

  

Teilnehmerliste:  

Interessenten sollen sich bitte in eine bei Frau Schuler ausliegende Liste eintragen, Raum 132, Di–Do, 9–13 Uhr und 14–16 :30 Uhr.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Der Einsatz von Unterrichtsmedien im Mathematikunterricht gewinnt sowohl auf der Ebene der Unterrichtsplanung, wie auch der der Unterrichtsrealisierung an Bedeutung. Die Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife (Beschluss der Kultusministerkonferenz vom 18.10.2012) heben das Potenzial digitaler Mathematikwerkzeuge explizit hervor : Die Entwicklung mathematischer Kompetenzen wird durch den sinnvollen Einsatz digitaler Mathematikwerkzeuge unterstützt. Das Potenzial dieser Werkzeuge entfaltet sich im Mathematikunterricht a) beim Entdecken mathematischer Zusammenhänge, insbesondere durch interaktive Erkundungen beim Modellieren und Problemlösen, b) durch Verständnisförderung für mathematische Zusammenhänge, nicht zuletzt mittels vielfältiger Darstellungsmöglichkeiten, c) mit der Reduktion schematischer Abläufe und der Verarbeitung größerer Datenmengen, d) durch die Unterstützung individueller Präferenzen und Zugänge beim Bearbeiten von Aufgaben einschließlich der reflektierten Nutzung von Kontrollmöglichkeiten.

Vor dem Hintergrund konstruktivistischer Lerntheorien zeigt sich, dass der reflektierte Einsatz unter anderem von Computerprogrammen die mathematische Begriffsbildung nachhaltig unterstützen kann. So erlaubt beispielsweise das Experimentieren mit Computerprogrammen mathematische Strukturen zu entdecken, ohne dass dies von einzelnen Routineoperationen (wie z.B. Termumformung) überdeckt würde. Es ergeben sich daraus tiefgreifende Konsequenzen für den Mathematikunterricht. Von daher setzt sich dieses Seminar zum Ziel, den Studierenden die notwendigen Entscheidungs- und Handlungskompetenzen zu vermitteln, um zukünftige Mathematiklehrer auf ihre berufliche Tätigkeit vorzubereiten.

Ausgehend von ersten Überlegungen zur Unterrichtsplanung werden anschließend Computer und Handheld hinsichtlich ihres jeweiligen didaktischen Potentials untersucht. Die dabei exemplarisch vorgestellten Systeme sind :

Neben der regelmäßigen Teilnahme an den Seminarveranstaltungen werden der zweimalige Besuch des Didaktischen Seminars und das Bestehen einer Abschlussklausur erwartet.________________________________________

Typisches Semester:  

nach dem Praxissemester

ECTS-Punkte:  

4 Punkte

Sprechstunde Dozent:  

n.V.
 
     
SS2016 PIC_________________________________________________________

Fachdidaktikseminar:  

Analysis verstehen und verständlich unterrichten

  

Dozent:  

Prof. Dr. Timo Leuders

  

Dozent:  

JProf. Dr. Michael Besser
  

Zeit/Ort:  

Mi 8–10 Uhr, SR 125, Eckerstr. 1

  

Teilnehmerliste:  

Interessenten sollen sich bitte in eine bei Frau Schuler ausliegende Liste eintragen, Raum 132, Di–Do, 9–13 Uhr und 14–16 :30 Uhr.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/didaktik/

  
 
_______________________________________________________________

Inhalt:
Analysis bildet einen wesentlichen Bestandteil des Mathematikunterrichts der gymnasialen Oberstufe. Das Seminar soll Studierenden Anregungen geben, wie man Schülerinnen und Schülern ein sinnstiftendes, kompetenzorientiertes und erfolgreiches Lernen von Analysis ermöglicht. Folgende Themenbereiche bilden den inhaltlichen Kern der Veranstaltung (stets unter Berücksichtigung des aktuellen Forschungsstands zum Lehren und Lernen von Analysis) :

1.
Analysis verstehen : Die Bedeutungen der zentralen Begriffe der Analysis erschöpfen sich nicht in ihrer formalen Definition. Hier gibt es zahlreiche Begriffsaspekte, Vorstellungen, Eigenschaften, Sichtweisen und Anwendungen, die das Verständnis dieser Begriffe vertiefen können. Welche sind diese ? Wie sehen die Brücken zur Schulmathematik aus ?
2.
Schülerdenken verstehen : Welche Lernvoraussetzungen haben Lernende zu Beginn der Analysis, insbesondere im Bereich Funktionen und Algebra ? Mit welchen typischen Schwierigkeiten und Fehlern muss man rechnen ? Wie kann man damit umgehen ?
3.
Analysis verständlich unterrichten : Wie sehen gute Aufgaben in der Analysis aus ? Wie können Lernende die wichtigsten Konzepte selbständig entdecken ? Welche unterschiedlichen Zugänge zur Analysis wurden in den letzten Jahrzehnten international vorgeschlagen ?
______________________________________________________________________________________________

Typisches Semester:  

nach dem Praxissemester

ECTS-Punkte:  

4 Punkte

Sprechstunde Dozent:  

n.V.
 

PIC    

Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Prakt. Übung zu:  

Numerik (2. Teil der zweisemestrigen Veranstaltung)

  

Dozent:  

Prof. Dr. S. Bartels

  

Zeit/Ort:  

CIP-Pool Raum 201, Hermann-Herder-Str. 10
2-std. (14-tägl.) n. V.

  

Tutorium:  

Dipl.-Math. A. Papathanssopoulos

  

Web-Seite:  

http://aam.uni-freiburg.de/bartels

  
 
_______________________________________________________________

Inhalt:
In der praktischen Übung zur Numerik-Vorlesung sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C sowie mit Hilfe der kommerziellen Software Matlab zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)
S. Bartels : Numerik 3x9. Springer, 2016.
2.)
R. Plato : Numerische Mathematik kompakt. Vieweg, 2006.
3.)
R. Schaback, H. Wendland : Numerische Mathematik. Springer, 2004.
4.)
J. Stoer, R. Burlisch : Numerische Mathematik I, II. Springer, 2007, 2005.
5.)
G. Hämmerlin, K.-H. Hoffmann : Numerische Mathematik. Springer, 1990.
6.)
P. Deuflhard, A. Hohmann, F. Bornemann : Numerische Mathematik I, II. DeGruyter, 2003.
_

Typisches Semester:  

4. Semester

ECTS-Punkte:  

(für Teile 1 und 2 zusammen) 3 Punkte

Notwendige Vorkenntnisse:  

Vorlesung Numerik (parallel)

Sprechstunde Dozent:  

Mi 12–13 Uhr, Zi. 209, Hermann-Herder-Str. 10, u. n.V.

Sprechstunde Assistent:  

Di 11–12 Uhr, Zi. 208, Hermann-Herder-Str. 10, u. n.V.

 
PIC
SS2016 PIC_________________________________________________________

Prakt. Übung zu:  

Stochastik

  

Dozent:  

N. N.

  

Zeit/Ort:  

Fr 14–16 Uhr, HS Weismann-Haus, Albertstr. 21a

  

Tutorium:  

Jonathan Ansari

  

Vorbesprechung:  

In der ersten Vorlesung Stochastik.
  

Teilnehmerliste:  

Eine Anmeldung über das Studierendenportal http://campus.uni-freiburg.de ist erforderlich, sie ist während der ersten Vorlesungswoche möglich.

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/Vorlesungen/vvSS2016/PraStoch/

  
 
_______________________________________________________________

Inhalt:
Die praktische Übung richtet sich an Hörer der Vorlesung Stochastik. Es werden computer-basierte Methoden diskutiert, die das Verständnis des Stoffes der Vorlesung vertiefen. Die praktische Übung wird auf der Basis des frei verfügbaren Statistik-Paketes R durchgeführt.

Nach einer Einführung in R werden Verfahren der deskriptiven Statistik und der graphischen Darstellung und Auswertung von Daten erläutert. Programmierkenntnisse werden nicht vorausgesetzt. Im zweiten Teil werden sowohl parametrische als auch nichtparametrische Testverfahren sowie Verfahren der linearen Regressions- und der Varianzanalyse diskutiert.

Die praktische Übung ist für Bachelor-Studierende verpflichtend.

Es werden die Laptops der Studierenden eingesetzt. Idealerweise sollte auf diesen dazu bereits R sowie ein VPN-Client für den Zugang zum WLAN der Uni Freiburg installiert sein. Entsprechende Links zum Download der Software sowie Hinweise zur Installation unter Linux, Mac OS X und Windows finden Sie auf der Webseite der Veranstaltung http://www.stochastik.uni-freiburg.de/Vorlesungen/vvSS2016/PraStoch/.________

Typisches Semester:  

4. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Analysis I u. II ; Lineare Algebra I u. II, Stochastik (1. Teil)

Sprechstunde Dozent:  

n.V., Eckerstr. 1

Sprechstunde Assistent:  

Mo 12–14 Uhr, Mi 10–12 Uhr, Zi. 228, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Prakt. Übung zu:  

Numerik für Differentialgleichungen

  

Dozent:  

Prof. Dr. Patrick Dondl

  

Zeit/Ort:  

2-std. (14-tägl.) n. V., CIP-Pool 201, Hermann-Herder-Str. 10

  

Tutorium:  

N. N.

  

Web-Seite:  

http://aam.uni-freiburg.de/abtlg/ls/lsdo/lv/numdgl_ss16

  
 
_______________________________________________________________

Inhalt:
In der praktischen Übung zur Vorlesung über die Numerik für Differentialgleichungen sollen die in der Vorlesung entwickelten und analysierten Algorithmen praktisch umgesetzt und getestet werden. Dies wird in der Programmiersprache C++ sowie mit Hilfe der kommerziellen Software MATLAB zur Lösung und Visualisierung mathematischer Probleme geschehen. Elementare Programmierkenntnisse werden vorausgesetzt.

Literatur:

1.)
R. Plato : Numerische Mathematik kompakt. Vieweg 2006
2.)
R. Schaback, H. Wendland : Numerische Mathematik. Springer 2004.
3.)
J. Stoer, R. Bulirsch : Numerische Mathematik I, II. Springer 2007, 2005.
4.)
W. Walter : Gewöhnliche Differentialgleichungen : Eine Einführung. Springer 2000.
5.)
M. Hanke-Bourgeois : Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Vieweg+Teubner 2006.
_____________________________________________________________________________

Typisches Semester:  

4. Semester

ECTS-Punkte:  

1 (zusammen mit Vorlesung und Übung 6) Punkte

Notwendige Vorkenntnisse:  

Vorlesung Numerik für Differerentialgleichungen (parallel)

Sprechstunde Dozent:  

Wird in der Vorlesung bekannt gegeben

Sprechstunde Assistent:  

Wird in der Vorlesung bekannt gegeben

 

 

3. Seminare

Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Proseminar:  

Fourier-Analysis

  

Dozent:  

Prof. Dr. Ernst Kuwert

  

Zeit/Ort:  

Di 8–10 Uhr, SR 125, Eckerstr. 1

  

Tutorium:  

Dr. Christian Ketterer

  

Vorbesprechung:  

Do, 04.02.2016, 10 :15 Uhr, SR 119, Eckerstr. 1

  

Teilnehmerliste:  

E-Mail an ludmilla.frei@math.uni-freiburg.de bis 03.02.2016

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
Für periodische Funktionen hat die Darstellung als Fourierreihe

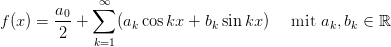
a ∞∑ f(x) = -0+ (ak cos kx + bk sinkx ) mit ak,bk ∈ ℝ 2 k=1
eine fundamentale Bedeutung. Motivationen aus der Physik sind z.B. die Beschreibung der schwingenden Saite und der Wärmeleitung. Die Frage der punktweisen Konvergenz ist bei Fourierreihen subtil. Ein ganz klares Bild ergibt sich aber, wenn man das L2-Skalarprodukt
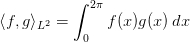
∫ 2π ⟨f, g⟩ 2 = f (x)g(x)dx L 0
ins Spiel bringt. Als Anwendungen behandeln wir auch das isoperimetrische Problem und einen Satz von Weyl über die Gleichverteilung für irrationale Zahlen.

Das Proseminar wendet sich auch (aber nicht nur) an Studierende im 2. Semester.

Literatur:

1.)
Stein & Shakarchi, Fourier Analysis (An Introduction), Princeton 2003.
________________________________________________________________________________________

Typisches Semester:  

ab 2. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Analysis I, Lineare Algebra I

Prüfungsleistung:  

Vortrag

Sprechstunde Dozent:  

Mi 11 :15–12 :15 Uhr, Zi. 208, Eckerstr. 1

Sprechstunde Assistent:  

Do 10–12 Uhr, Zi. 213, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Proseminar:  

Gewöhnliche Differentialgleichungen

  

Dozent:  

Prof. Dr. Michael Růžička

  

Zeit/Ort:  

Fr 14–16 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

Dr. Philipp Nägele

  

Vorbesprechung:  

zusätzlicher Termin : Mo, 15. Februar, 11 :00 Uhr, SR 127

  

Teilnehmerliste:  

Bei Frau Ruf, Zi. 205, Hermann-Herder-Str. 10

  

Web-Seite:  

http://aam.uni-freiburg.de/lehre/ss16/prosem_dgl

  
 
_______________________________________________________________

Inhalt:
Der zeitliche Verlauf einer Vielzahl alltäglicher Phänomene (Populationswachstum, Abkühlung von Kaffee, Räuber-Beute Modelle, …) lässt sich durch Anfangswertprobleme der Form

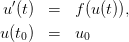
u′(t) = f(u(t)), u(t) = u 0 0
beschreiben. Dabei sind f und u0 gegebene Funktionen und gesucht ist eine Funktion u, die sowohl die gewöhnliche Differentialgleichung löst, als auch den Anfangswert annimmt.

Im Proseminar wollen wir uns zuerst mit der Existenz und Eindeutigkeit von Lösungen von Anfangswertproblemen beschäftigen und Lösungsmethoden kennenlernen. Anschließend soll die Theorie auf Systeme gewöhnlicher Differentialgleichungen erweitert, daneben aber auch auf konkrete Beispiele angewendet werden. Bei Interesse kann auch noch auf die numerische Approximation von gewöhnlichen Differentialgleichungen eingegangen werden.

Da gewöhnliche Differentialgleichungen Stoff der Kursstufe an Gymnasien sind, richtet sich das Proseminar insbesondere auch an Lehramtsstudierende.

Literatur:

1.)
Walter, Wolfgang, Gewöhnliche Differentialgleichungen, Springer.
2.)
Aulbach, Bernd, Gewöhnliche Differentialgleichungen, Spektrum Akademischer Verlag
3.)
Strogatz, Steven, Nonlinear Dynamics and Chaos, Westview Press
________________________________________________________________________________________

Typisches Semester:  

ab 3. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Grundvorlesungen Analysis und lineare Algebra

Sprechstunde Dozent:  

Mi 13–14 Uhr und n.V., Zi. 145, Eckerstr. 1

Sprechstunde Assistent:  

jederzeit n.V., Zi. 147, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Proseminar:  

Nichtlineare Dynamik und Chaos

  

Dozentin:  

Katrin Wendland

  

Zeit/Ort:  

Mo 14–16 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

Anda Degeratu

  

Vorbesprechung:  

Mi, 10.02.2016, 11 :00 Uhr, SR 414, Eckerstr. 1
Bitte kommen Sie zur Vorbesprechung, falls Sie daran interessiert sind, einen Vortrag zu übernehmen. Vorab wird keine Teilnehmerliste angelegt.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/mathphys/lehre/SoSe16/chaos.html

  
 
_______________________________________________________________

Inhalt:
The focus of this seminar is an introduction to nonlinear dynamics with an emphasis on applications to physics, engineering, biology, and chemistry.

The main object of study are systems of ordinary differential equations. When the system is linear, like the case of the simple harmonic oscillator, mẍ + kx = 0, describing the vibrations of a mass hanging from a linear spring, an explicit solution is easy to write down. When not, then we are in the nonlinear case and then it is often hard to write down a solution. Even when we succeed in this endeavour, like in the case of the pendulum, ẍ + k sin x = 0, the result is often impenetrable. During this seminar we will learn how to use a combination of analytical methods and geometrical thinking to infer predictions about the behaviour of the solutions, i.e. about the dynamics of the system. We will see that such a system can either settle down to an equilibrium, or it can repeat itself in cycles (and it is thus periodic), or it can exhibit an aperiodic, seemingly unpredictable behaviour (and it is thus chaotic). All these types of behaviours will be illustrated with concrete examples from applied sciences. However, no familiarity with physics, biology, or chemistry is going to be assumed, and everything will be built up from scratch. The prerequisites are knowledge of calculus (graphs of functions, multivariable functions and their partial derivatives, the Jacobian of a function, Taylor series) and linear algebra (matrices, eigenvectors, and eigenvalues).

The seminar will cover Chapter 1 to Chapter 9 of Strogatz’ book, “Nonlinear Dynamics and Chaos : with applications to physics, biology, chemistry, and engineering”. The talks will be in the language of choice of the speaker : either English or German.

Literatur:

1.)
Steven H. Strogatz, Nonlinear Dynamics and Chaos : with applications to physics, biology, chemistry, and engineering, Westview Press, 2001
________________________________________________________

Typisches Semester:  

ab dem 4. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Lineare Algebra und Analysis I/II

Studienleistung:  

Regelmäßige Teilnahme

Prüfungsleistung:  

Vortrag

Sprechstunde Dozentin:  

Mi 13–14 Uhr, Zi. 337, Eckerstr. 1.

Sprechstunde Assistentin:  

Di 14–16 Uhr, Zi. 328, Eckerstr. 1.

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Proseminar:  

Ungleichungen und Abschätzungen

  

Dozentin:  

JProf. Dr. Nadine Große

  

Zeit/Ort:  

Mi 10–12 Uhr, SR 125, Eckerstr. 1

  

Tutorium:  

Dr. Doris Hein

  

Vorbesprechung:  

Di 09.02.2016, 14 :30 Uhr, SR 318, Eckerstr. 1
  

Teilnehmerliste:  

Bitte tragen Sie sich bis 08.02.2016 in eine bei Frau Wöske (Zi. 336, Mo–Mi 12–16 Uhr, Fr 8–12 Uhr) ausliegende Liste ein.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/ngrosse/teaching/Prosem_Ungl.html

  
 
_______________________________________________________________

Inhalt:
 
In vielen Bereichen der Mathematik kann die Lösung des Problems nur abgeschätzt werden, z.B. bei Extremwertaufgaben, Eigenwertabschätzungen oder Differentialgleichungen. Im Seminar werden wichtige Ungleichungen, z.B. die Cauchy-Schwarzsche, die Jensensche Ungleichung und deren Anwendungen, behandelt. Weitere Schwerpunkte sind Eigenwertabschätzungen von Matrizen und Ungleichungen der Analysis._____________________________________________________________

Typisches Semester:  

ab 2. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Lineare Algebra II, Analysis II

Sprechstunde Dozent:  

Mi 13 :10–13 :55 Uhr, Zi. 325, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 323, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Proseminar:  

Geometrie und Symmetrie

  

Dozent:  

Prof. Dr. W. Soergel

  

Zeit/Ort:  

Fr 8–10 Uhr, SR 404, Eckerstr. 1

  

Tutorium:  

N. N.

  

Vorbesprechung:  

Mo, 01.02.2016, 9 :00–10 :00 Uhr, SR 404, Eckerstr. 1

  
 
_______________________________________________________________

Inhalt:
Im Proseminar sollen verschiedene Themen besprochen werden, die um diese Begriffe kreisen. Ich denke etwa an Möbius-Geometrie, Spiegelungsgruppen, Konvexgeometrie, Inzidenzgeometrie und dergleichen mehr.______________________________________________________________________________________________

Typisches Semester:  

4. Semester

ECTS-Punkte:  

3 Punkte

Notwendige Vorkenntnisse:  

Grundvorlesungen

Sprechstunde Dozent:  

Mi 12 :30–13 :30 Uhr, Raum 429, Eckerstr. 1

 

Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Differentialgeometrie

  

Dozent:  

Prof. Dr. V. Bangert

  

Zeit/Ort:  

Fr 14–16 Uhr, SR 404, Eckerstr. 1

  

Tutorium:  

Dr. B. Mramor

  

Vorbesprechung:  

Fr, 12.02.2016, 13 :00 Uhr, SR 404, Eckerstr. 1.
  

Teilnehmerliste:  

Bitte tragen Sie sich in eine Liste ein, die von Montag, 25.01.2016, bis Freitag, 05.02.2016, bei Frau Wöske (Zi. 336, Mo–Mi 12–16 Uhr, Fr 8–12 Uhr) ausliegt.

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/geometrie/lehre/ss2016/seminar/Differentialgeometrie/index.html

  
 
_______________________________________________________________

Inhalt:

Das Seminar richtet sich an Studierende des Bachelor- oder Lehramtsstudiengangs, die Vorkenntnisse über differenzierbare Mannigfaltigkeiten und Riemannsche Metriken haben im Umfang der Vorlesung Differentialgeometrie I aus dem WS 2015/16. Die Vortragsthemen sind so gewählt, dass sie mit diesen Vorkenntnissen bearbeitet werden können. Themen und Literatur zu denVorträgen werden in der Vorbesprechung bekannt gegeben. Die Vorträge können mit der Anfertigung einer Bachelorarbeit verbunden werden.___________________________________________________________________________________________________________

Typisches Semester:  

6. FS im Bachelorstudiengang

Notwendige Vorkenntnisse:  

Differentialgeometrie I

Nützliche Vorkenntnisse:  

Elementare Differentialgeometrie, Topologie

Prüfungsleistung:  

Vortrag

Sprechstunde Dozent:  

Di 14–15 Uhr, Zi. 335, Eckerstr. 1

Sprechstunde Assistent:  

Fr 8–12 Uhr, Zi. 327, Eckerstr. 1

 
PIC
SS2016 PIC_________________________________________________________

Seminar:  

Finance aus der Praxisperspektive

  

Dozentin:  

Prof. Dr. Eva Lütkebohmert-Holtz

  

Dozent:  

Prof. Dr. Thorsten Schmidt
  

Zeit/Ort:  

Di 14–16 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

Sandrine Gümbel ; Julian Sester

  

Vorbesprechung:  

Mi, 10.02.2016, 13 :00 Uhr, Raum 232, Eckerstr. 1

  

Teilnehmerliste:  

Per E-Mail mit kompletten Bewerbungsunterlagen (siehe Homepage) an sandrine.guembel@stochastik.uni-freiburg.de oder julian.sester@finance.uni-freiburg.de bis Mo, 08.02.2016.

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/professoren/schmidt/ida_2015

  
 
_______________________________________________________________

Inhalt:
Fachübergreifendes und praxisnahes Lernen : Das ist das Ziel des didaktischen Projekts für die Masterstudiengänge Volkswirtschaftslehre, Economics und Mathematik. Studierende aus unterschiedlichen Disziplinen sollen gemeinsam Lösungen für Probleme aus der Praxis erarbeiten und umsetzen. Dabei arbeiten sie in fachübergreifenden Kleingruppen an verschiedenen Projekten, die teilweise in Kooperation mit Banken und Versicherungen entwickelt werden. Hierdurch wird einerseits eine dem späteren Berufsalltag nachempfundene Situation hergestellt und andererseits die praktische Anwendungskompetenz von im Studium erworbenen Kenntnissen gezielt gefördert.

Die Ergebnisse der verschiedenen Projekte sollen von den Teilnehmerinnen und Teilnehmern regelmäßig im Kurs präsentiert werden und gegenseitig ausgewertet werden. Durch die stark interdisziplinäre und projektbasierte Arbeitsweise an praxisrelevanten Aufgaben will das Konzept die Studierenden zum Selbststudium anregen und intensiv auf die spätere Berufswelt vorbereiten.

Das IDA-Seminar wird im SS 2016 stattfinden und beinhaltet die über 4×4 Wochen gehende Bearbeitung von kleineren Projekten in interdisziplinären Teams aus 4 Personen. Die Themen werden von Praxispartnern gestellt und etwaige Spezialkenntnisse vorab in einem Blockkurs vermittelt. Im Anschluss können möglicherweise Themen weiter verfolgt werden, wie etwa in einer Masterarbeit oder einem Praktikum.

Eine Anmeldung ist unbedingt erforderlich, siehe Homepage !______________________________________

Typisches Semester:  

ab dem 1. Semester im Master

Sprechstunde Dozentin:  

n.V., Zi. 2314, KG II, Platz der Alten Synagoge

Sprechstunde Dozent:  

n.V., Raum 247, Eckerstr. 1

Sprechstunde Assistentin:  

n.V., Zi. 223, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 2032, KG II, Platz der Alten Synagoge

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Funktionenkörper

  

Dozent:  

Prof. Dr. Annette Huber-Klawitter

  

Zeit/Ort:  

Mo 14–16 Uhr, SR 125, Eckerstraße 1

  

Tutorium:  

Dr. Oliver Bräunling

  

Vorbesprechung:  

Mo, 15.02.2016, 09 :00 Uhr, SR 404, Eckerstr. 1

  

Teilnehmerliste:  

bei Frau Frei (Zi. 433, Eckerstr. 1), bei Überbelegung werden Lehramtsstudenten bevorzugt

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/arithgeom/lehre/ss16/functionfields/webtext.htm

  
 
_______________________________________________________________

Inhalt:
Wie würden Sie den Begriff “Kurve” definieren ? Als Beispiel : Einen Kreis könnte man sowohl als Bild von

γ[0, 2π] → R2, α ↦→ (sin α,cosα )

oder aber auch als Nullstellenmenge von x2 + y2 - 1 im R2 definieren. Aber keine dieser Darstellungen ist besonders kanonisch. Allein schon durch eine andere Wahl von Koordinaten im R2 würden wir völlig andere Formeln bekommen. Diese Probleme kann man auf elegante Weise lösen, indem man einen anderen Blickwinkel einnimmt : Auf einem geometrischen Gebilde kann man Funktionen betrachten, die (nach sorgfältiger Begriffsbildung) einen Körper bilden. Entwickelt man diesen Standpunkt, entpuppt sich schnell, dass es völlig genügt mit einem abstrakten Körper zu arbeiten, dessen Elemente a priori rein gar nichts mit Funktionen zu tun haben müssen, und dass “endlich erzeugte Körper-Erweiterungen von Transzendenzgrad eins” eine erstaunlich nützliche Definition für (normale algebraische) Kurven ist. In dem Seminar werden wir die Geometrie von Kurven von diesem Standpunkt entwickeln. 

Dieses Seminar richtet sich besonders an Lehramtsstudiengänge.

Literatur:

1.)
LANG, SERGE Introduction to Algebraic and Abelian Functions, 2nd edition, 089 (GTM series), Springer, 1995
2.)
LANG, SERGE Elliptic Functions, 2nd edition, 112 (GTM series), Springer, 1987
3.)
LORENZ, FALKO Algebraische Zahlentheorie, Spektrum Akademischer Verlag, 1993
4.)
ROSEN, MICHAEL Number Theory in Function Fields, GTM series, Springer, 2002

Wir werden hauptsächlich Langs Buch “Introduction to Algebraic and Abelian Functions” folgen. Das Buch von Rosen, Kapitel 5–7, enthält z.T. ähnliches Material, aber anders aufbereitet.

_____________________________________________

Typisches Semester:  

ab 4. Semester

Notwendige Vorkenntnisse:  

Algebra

Nützliche Vorkenntnisse:  

Funktionentheorie

Folgeveranstaltungen:  

Veranstaltungen zur algebraischen Geometrie, Algebraische Zahlentheorie

Sprechstunde Dozentin:  

Di 10 :30–11 :30 Uhr, Zi. 434, Eckerstr. 1

Sprechstunde Assistent:  

Mo 12–14 Uhr, Zi. 436, Eckerstr. 1

Kommentar:  

Interessenten sollten sich frühzeitig in die vorläufige Teilnehmerliste bei Frau Frei eintragen. Bei Überbelegung der verfügbaren Plätze werden Lehramtsstudenten bevorzugt.
Lehramtsstudenten, die Interesse haben, ihre Abschlussarbeit in diesem Thema zu schreiben, sollten dies bereits in dieser vorläufigen Teilnehmerliste anmerken.

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Geometrische Variationsrechnung

  

Dozent:  

Prof. Dr. Guofang Wang

  

Zeit/Ort:  

Mi 16–18 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

J. Scheuer

  

Vorbesprechung:  

Mi, 10.02.2016, 14–16 Uhr, SR 404, Eckerstr. 1

  

Web-Seite:  

http://www.mathematik.uni-freiburg.de/home/Wang

  
 
_______________________________________________________________

Inhalt:
 
Variationsrechnung ist eines der ältesten Teilgebiete der Analysis. In der Variationsrechnung geht es darum, Extremstellen von Funktionalen zu finden. Viele Fragestelle aus der Geometrie (Geodätischen, d.h. kürzeste Verbindung zwischen zwei Punkten ; Minimalflächen), der partiellen Differentialgleichungen, und der Physik (klassischen Mechanik, Optik und Feldtheorie) führen auf unendlichendimensionale Extremwertaufgaben. In dem Seminar werden die direkte Methode, sowie die Minimax-Methode untersucht.

Literatur:

1.)

Struwe, Variational methods. Third edition. Ergebnisse der Mathematik und ihrer Grenzgebiete, 4. Folge, A Series of Modern Surveys in Mathematics, 34, Springer-Verlag, Berlin, 2008

__________________________________________________________________________________________________________________________

Typisches Semester:  

ab 6.

Notwendige Vorkenntnisse:  

Funktionalanalysis oder partielle Differentialgleichungen

Sprechstunde Dozent:  

Mi 11 :15–12 :15 Uhr, Zi. 209, Eckerstr. 1

Sprechstunde Assistent:  

Di 10–12 Uhr, Zi. 206, Eckerstr. 1

 
Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Kommutative Algebra und Algebraischen Geometrie

  

Dozent:  

Prof. Dr. Stefan Kebekus

  

Zeit/Ort:  

Mi 10–12 Uhr, SR 403, Eckerstr. 1

  

Tutorium:  

Dr. Hannah Bergner

  

Vorbesprechung:  

Fr, 12.02.2016, 14 Uhr, SR 119, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/kebekus/

  
 
_______________________________________________________________

Inhalt:
Das Seminar zur Kommutativen Algebra und Algebraischen Geometrie ergänzt die Vorlesung "Kommutative Algebra und Einführung in die Algebraische Geometrie", die parallel angeboten wird, kann aber unabhängig von der Vorlesung belegt werden. Ziel ist es, die enge Verbindung von Algebra und Geometrie zu beleuchten, und die abstrakten Begriffsbildungen der kommutativen Algebra durch geometrische Beispiele zu erläutern.

Das Seminar eignet sich insbesondere für Studenten, die eine Abschlussarbeit in komplexer oder algebraischer Geometrie erwägen.

Literatur:

1.)
Andreas Gathmann : Algebraic Geometry, http://www.mathematik.uni-kl.de/agag/mitglieder/professoren/gathmann/notes/alggeom/
2.)
Igor Dolgachev : Introduction to Algebraic Geometry, http://www.math.lsa.umich.edu/~idolga/lecturenotes.html
_______________________

Typisches Semester:  

ab dem 4. Semester

Notwendige Vorkenntnisse:  

Algebra und Zahlentheorie

Studienleistung:  

Regelmäßige Teilnahme

Prüfungsleistung:  

Vortrag

Sprechstunde Dozent:  

Mi 13–14 Uhr, Zi. 432, Eckerstr. 1

Sprechstunde Assistentin:  

Di 14–17 Uhr, Zi. 422, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Mathematische Modellierung von Mehrphasenströmungen mit Phasenübergang

  

Dozent:  

Prof. Dr. D. Kröner

  

Zeit/Ort:  

Di 16–18 Uhr, SR 226, Hermann-Herder-Str. 10

  

Tutorium:  

N. N.

  

Vorbesprechung:  

Di, 02.02.2016, 16 :15 Uhr, SR 226, Hermann-Herder-Str. 10

  

Web-Seite:  

http://aam.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
In diesem Seminar betrachten wir Mehrphasenströmungen mit Phasenübergängen. Wenn man z. B. einen Tropfen Öl in ein Glas Wasser gibt, bewegt sich der Öltropfen im Wasser, ohne sich mit dem Wasser zu vermischen. In diesem Falle hat man eine Zweiphasenströmung ohne Phasenübergang. In kochendem Wasser ist die Situation anders. In diesem Fall steigen Dampfblasen im Wasser auf und verschwinden durch Kondensation, wenn sie in kältere Bereiche kommen. In diesem Fall geht es um eine Zweiphasenströmung mit Phasenübergang. Hierzu gibt es verschiedene mathematische Modelle. Sie bestehen alle aus einem System von partiellen Differentialgleichungen, deren zentraler Teil aus den kompressiblen oder inkompressiblen Navier-Stokes-Gleichungen mit gewissen Modifikationen bestehen.

In diesem Seminar werden wir einige Modelle herleiten, Existenz- und Eindeutigkeitsfragen und numerische Algorithmen analysieren. Insbesondere werden wir die Eigenschaften der Lösung an der Phasengrenze untersuchen._____________________________________________________________________________

Typisches Semester:  

ab 5. Semester

Notwendige Vorkenntnisse:  

Numerik I, II ; Numerik für Differentialgleichungen ; Theorie und Numerik für partielle Differentialgleichungen

Sprechstunde Dozent:  

Mi 11–12 Uhr und n.V., Zi. 215, Hermann-Herder-Str. 10

Sprechstunde Assistent:  

n.V.

 
PIC      
Abteilung für
Mathematische Logik
SS2016 PIC_________________________________________________________

Seminar:  

Properes und stark properes Forcing

  

Dozentin:  

Heike Mildenberger

  

Zeit/Ort:  

Mo 16–18 Uhr, SR 125, Eckerstr. 1

  

Tutorium:  

Giorgio Laguzzi

  

Vorbesprechung:  

Mo, 08.02.2016, 13 Uhr, Zi. 310, Eckerstr. 1

  

Teilnehmerliste:  

bei Frau Samek, Zi. 312, bis zum 02.02.2016

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/mildenberger/veranstaltungen/ss16/forcingseminar.html

  
 
_______________________________________________________________

Inhalt:
 
Etwa im Jahr 1980 definierte Shelah die Eigenschaft Properness für Forcinghalbordnungen. Properness ist eine Abschwächung der Antiketteneigenschaft (“c.c.c.”). Propere Forcings erhalten unter anderem ℵ1 als Kardinalzahl und lassen sich mit abzählbaren Trägern iterieren. Im Jahr 2002 führten Friedman und Mitchell unabhängig voneinander stark propere Forcings ein. 2012 fand Neeman zahlreiche neuartige Forcings, die Properness mit starker Properness kombinieren und die gestatten, Properness in geeigneten Iterationen mit endlichen Trägern zu erhalten.

In diesem Seminar studieren wir zuerst einige grundlegende Eigenschaften dieser Forcings und gehen dann zu Anwendungen aus dem Themenkreis der Kombinatorik der stationären Mengen über. Es können Bachelor-, Master- und Staatsexamensarbeiten vergeben werden, d.h., das Seminar ist auch als Bachelorseminar geeignet.

Literatur:

1.)
Uri Abraham und Saharon Shelah. Forcing closed unbounded sets. J. Symbolic Logic 48 (1983), no. 3, 643–657.
2.)
Uri Abraham, Proper Forcing, in : Handbook of Set Theory, eds. M. Foreman, A. Kanamori, Springer 2010, 333–394.
3.)
Sy-David Friedman, Forcing with finite conditions, in : Set Theory, Trends in Mathematics, eds. J. Bagaría, S. Todorčević, Birkhäuser, 2006, 285–295.
4.)
Itay Neeman, Forcing with sequences of models of two types. Notre Dame J. Form. Log. 55 (2014), no. 2, 265–298.
5.)
Saharon Shelah, Proper Forcing, Lecture Notes in Mathematics, 940. Springer-Verlag, Berlin-New York, 1982.
6.)
Saharon Shelah, Proper and Improper Forcing, Second edition. Perspectives in Mathematical Logic. Springer-Verlag, Berlin, 1998.
__________________________________________________________________________

Typisches Semester:  

ab dem 5. Semester

Notwendige Vorkenntnisse:  

Mathematische Logik, Mengenlehre

Sprechstunde Dozentin:  

Di 13–14 Uhr, Zi. 310, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 311, Eckerstr. 1

 
PIC      
Abteilung für
Mathematische Logik
SS2016 PIC_________________________________________________________

Seminar:  

Seminar über Modelltheorie

  

Dozent:  

Martin Ziegler
  

Zeit/Ort:  

Mi 8–10 Uhr, SR 318, Eckerstr. 1

  

Tutorium:  

Moshen Khani

  

Vorbesprechung:  

Mi, 10.02.2016, 9 :45 Uhr, SR 318, Eckerstr. 1

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/ziegler/veranstaltungen/ss16-seminar.html

  
 
_______________________________________________________________

Inhalt:
Wir behandeln den folgenden Satz von Denef und Van den Dries :

Sei An die Familie aller auf einer Potenz des Einheitsintervalls definierten analytischen Funktionen. Dann ist die Struktur

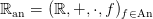
ℝan = (ℝ,+, ⋅,f)f∈An

o-minimal.

Das bedeutet, daß alle definierbare Teilmengen von ℝ endliche Vereinigungen von Intervallen sind. Wir folgen dabei einer Vorlesungsausarbeitung von Alex Wilkie.

Literatur:

1.)
A. Wilkie Lectures on elimination theory for semialgebraic and subanalytic sets, http://home.mathematik.uni-freiburg.de/ziegler/veranstaltungen/Wilkie.pdf
____

Typisches Semester:  

ab 5. Semester

ECTS-Punkte:  

9 Punkte

Notwendige Vorkenntnisse:  

keine

Sprechstunde Dozent:  

n.V., Zi. 313, Eckerstr. 1

Sprechstunde Assistent:  

n.V., Zi. 305, Eckrstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Infinite Games and Regular Sets

  

Dozent:  

Dr. G. Laguzzi

  

Zeit/Ort:  

Mi, 14–16 Uhr, SR 318, Eckerstr. 1

  

Tutorium:  

n. V.

  

Vorbesprechung:  

Mo, 11.02.2016, 14 Uhr, Zi. 311, Eckerstr. 1

  

Teilnehmerliste:  

bei Frau Samek, Zi. 312, bis zum 05.02.2016

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/giorgio/SS16-IGRS.html

  
 
_______________________________________________________________

Inhalt:
 
Game Theory deals with games of “finite dimension”. In Descriptive Set Theory one extends such a study to infinite games, i.e., games where the competition between two players runs infinitely many steps. The study of this kind of games is very useful in topology and measure theory, since the existence of winning strategies is strictly connected with the existence of regular sets. Moreover, many other tools from set theory can be used for a deep understanding of the subsets of the real line and more generally of Polish spaces. This seminar is intended to go into the study of this kind of questions, and it is meant to show a bridge from topology and measure theory on the one side, and set theory on the other side.

Literatur:

1.)
A. Kanamori, The Higher Infinite, Springer (1994).
2.)
T. Bartoszyński, H. Judah, Set Theory-On the structure of the real line, AK Peters Wellesley (1999).
3.)
A. Levy, Basic Set Theory, Springer (1979).
4.)
A. Kechris, Classical Descriptive Set Theory, Springer (1995)
5.)
J. Brendle, B. Löwe, Solovay-Type characterizations for Forcing-Algebra, Journal of Simbolic Logic, Vol. 64 (1999), pp. 1307–1323.
________________________________________________________________________

Typisches Semester:  

ab dem 3. oder 5. Semester

Sprechstunde Dozent:  

Di 13–14 Uhr, Zi. 311, Eckerstr. 1

 
PIC
SS2016 PIC_________________________________________________________

Seminar:  

Stochastik

  

Dozent:  

Peter Pfaffelhuber
  

Dozent:  

Thorsten Schmidt

  

Zeit/Ort:  

Blockveranstaltung, n. V., Zi. 232, Eckerstr. 1

  

Tutorium:  

Peter Czuppon ; Wahid Khosrawi-Sardroudi

  

Vorbesprechung:  

Mo, 08.02.2016, 15 :00 Uhr, Zi. 232, Eckerstr. 1

  

Teilnehmerliste:  

Interessenten werden gebeten, sich bis zum 05.02.2016 in eine Liste im Sekretariat (Zi. 226 oder Zi. 245, Eckerstr. 1) einzutragen.

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
Aufbauend auf der Vorlesung Wahrscheinlichkeitstheorie werden in dieser Veranstaltungen Themen für eine erste Abschlussarbeit in Mathematik (Bachelor oder Zulassungsarbeit) vorgestellt. Die Themen können sowohl direkt an die Vorlesung Wahrscheinlichkeitstheorie anschließen als auch Anwendungen enthalten, z.B. aus den Themenbereichen Finanzmathematik, Statistik oder biologischen Prozessen.____________________________________________________________________

Typisches Semester:  

ab dem 6. Semester

Notwendige Vorkenntnisse:  

Wahrscheinlichkeitstheorie

Sprechstunde Dozent:  

Pfaffelhuber : Mo 13 :15 Uhr, Zi. 233, Eckerstr. 1

Sprechstunde Dozent:  

Schmidt : n.V., Zi. 247, Eckerstr. 1

Sprechstunde Assistent:  

Czuppon : n.V., Zi. 231a, Eckerstr. 1

Sprechstunde Assistent:  

Khosrawi : n.V., Zi. 224, Eckerstr. 1

 
PIC
SS2016 PIC_________________________________________________________

Seminar:  

Stochastische Modelle in der Biologie

  

Dozent:  

Peter Pfaffelhuber

  

Zeit/Ort:  

Mo 14–16 Uhr, Raum 232, Eckerstr. 1

  

Tutorium:  

Felix Hermann

  

Vorbesprechung:  

Mo, 08.02.2016, 9 :00 Uhr, Zi. 232, Eckerstr. 1
  

Teilnehmerliste:  

Interessenten werden gebeten, sich bis zum 05.02.2106 in eine Liste im Sekretariat (Zi. 226 oder Zi. 245, Eckerstr. 1) einzutragen.

  

Web-Seite:  

http://www.stochastik.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:
Viele Prozesse in der Natur, insbesondere in lebenden Systemen, unterliegen stochastischen Phänomenen. Beispielsweise spielt bei der Vererbung der zufällige Genaustausch eine wichtige Rolle, das zufällige Treffen von Molekülen bei biochemischen Reaktionen, oder die zufällige Ausbreitung von Krankheiten.

In diesem Seminar besprechen wir einige Modelle der Mathematischen, insbesondere der stochastischen Biologie. Aufgrund der Vielzahl an möglichen Themen kann das Seminar sowohl von Bachelor-, Master- als auch von LehramtskanididatInnen besucht werden.

Literatur:

1.)
D. Anderson, T. G. Kurtz. Stochastic Analysis of Biochemical Systems. Springer. 2015
2.)
R. Durrett. Branching Process Models of Cancer. Springer. 2015
3.)
M. Ullah, O. Wolkenhauer. Stochastic Approaches for Systems Biology. Springer, 2011
_______

Typisches Semester:  

ab dem 6. Semester

Notwendige Vorkenntnisse:  

Wahrscheinlichkeitstheorie

Nützliche Vorkenntnisse:  

Stochastische Prozesse

Sprechstunde Dozent:  

Mo 13 :15 Uhr, Zi. 233, Eckerstr. 1

Sprechstunde Assistent:  

Di, Mi 10–12 Uhr, Zi. 244, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Strömungsdynamik

  

Dozent:  

Prof. Dr. M. Růžička

  

Zeit/Ort:  

Mi 10–12 Uhr, SR 127, Eckerstr. 1

  

Tutorium:  

S. Eckstein

  

Vorbesprechung:  

zusätzlicher Termin : Mo, 15. Februar, 10 :00 Uhr, SR 127

  

Teilnehmerliste:  

Bei Frau Ruf, Zi. 205, Hermann-Herder-Str. 10

  

Web-Seite:  

http://aam.uni-freiburg.de/lehre/ss16/dynamik

  
 
_______________________________________________________________

Inhalt:

Im Seminar werden wir Techniken und Methoden zur Behandlung von Stokes- und Navier-Stokes-Gleichungen erarbeiten. Diese beinhalten sowohl theoretische als auch numerische Fragestellungen. Die behandelten Themen eignen sich als Grundlage für Bachelorarbeiten.______________________________________________________________________________________________

Typisches Semester:  

6. Semester

Notwendige Vorkenntnisse:  

Einführung in Theorie und Numerik Partieller Differentialgleichungen oder Funktionalanlysis

Nützliche Vorkenntnisse:  

partielle Differentialgleichungen

Sprechstunde Dozent:  

Mi 13–14 Uhr, Zi. 145, Eckerstr. 1

Sprechstunde Assistentin:  

Mo 14–17, Raum 149, Eckerstr. 1

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Seminar:  

Spektraltheorie und Operatorhalbgruppen

  

Dozent:  

Prof. Dr. Patrick Dondl

  

Zeit/Ort:  

Blockseminar, Termine nach Vereinbarung

  

Vorbesprechung:  

in der dritten Vorlesungswoche, n.V.

  

Web-Seite:  

http://aam.uni-freiburg.de/abtlg/ls/lsdo/lv/spekt_ss16/

  
 
_______________________________________________________________

Inhalt:
Die grundlegende Fragestellung in diesem Seminar ist die nach der Lösung des abstrakten Anfangswertproblems

} ∂tu(t) + Au (t) = 0 u (0 ) = u0 ∈ X
(1)

in einem Hilbertraum X für einen (nicht notwendigerweise beschränkten) linearen Operator A auf X. Formal ergäbe sich als Lösung u(t) = e-Atu 0. Es stellt sich also die Frage nach einer rigorosen Definition des Ausdrucks e-tA. Ist das Anfangswertproblem (1) in einem vernünftigen Sinne lösbar, so nennt man A einen Erzeuger und e-tA die von ihm erzeugte Halbgruppe.

Zur rigorosen Behandlung des obigen Problems führen wir zunächst Grundbegriffe über (unbeschränkte) abgeschlossene Operatoren und deren Spektraltheorie ein. Danach folgt die Definition der Begriffe Halbgruppe und Erzeuger. Mit diesen Begriffen ausgerüstet, beweisen wir dann die Sätze von Hille-Yosida und Lumer-Phillips, die eine vollständige Charakterisierung von Erzeugern von Halbgruppen geben. Danach folgen einzelne Anwendungen in der Quantenmechanik, sowie ein kurzer Einblick in die Störungstheorie.

Literatur:

1.)
D. Werner. Funktionalanalysis (Springer-Lehrbuch) (German Edition). Springer, 6th edition, 2008
2.)
M. Reed and B. Simon. Methods of Modern Mathematical Physics I : Functional Analysis. Academic Press, Inc., 1981
3.)
T. Kato. Perturbation Theory for Linear Operators (Classics in Mathematics). Springer, reprint of the corr. 2nd edition, 1995.
4.)
H. Brezis. Functional Analysis, Sobolev Spaces and Partial Differential Equati- ons (Universitext). Springer, 2011 edition, 2010.
5.)
E. B. Davies. One-Parameter Semigroups (L.M.S. Monographs). Academic Pr, 1980.
6.)
M. Reed and B. Simon. Methods of Modern Mathematical Physics II and IV, Academic Press, Inc., 1975/78.
____________________________________________________________________________________

Typisches Semester:  

ab 4.

ECTS-Punkte:  

6 Punkte

Notwendige Vorkenntnisse:  

Funktionalanalysis, auch parallel

Sprechstunde Dozent:  

wird bekannt gegeben

Sprechstunde Assistent:  

wird bekannt gegeben

 
 
4. Oberseminare, Projektseminare

und Kolloquien

Mathematisches Institut
SS2016 PIC_________________________________________________________

Lesekurs:  

„Wissenschaftliches Arbeiten“

  

Dozent:  

Alle Dozentinnen und Dozenten des Mathematischen Instituts

  

Zeit/Ort:  

nach Vereinbarung

  
 
_______________________________________________________________

Inhalt:
In einem Lesekurs „Wissenschaftliches Arbeiten“ wird der Stoff einer vierstündigen Vorlesung im betreuten Selbststudium erarbeitet. In seltenen Fällen kann dies im Rahmen einer Veranstaltung stattfinden ; üblicherweise werden die Lesekurse aber nicht im Vorlesungsverzeichnis angekündigt. Bei Interesse nehmen Sie vor Vorlesungsbeginn Kontakt mit einer Professorin/einem Professor bzw. einer Privatdozentin/einem Privatdozenten auf ; in der Regel wird es sich um die Betreuerin/den Betreuer der Master-Arbeit handeln, da der Lesekurs als Vorbereitung auf die Master-Arbeit dienen kann.

Der Inhalt des Lesekurses, die näheren Umstände sowie die zu erbringenden Studienleistungen (typischerweise regelmäßige Treffen mit Bericht über den Fortschritt des Selbststudiums, eventuell Vorträge in einer Arbeitsgruppe (einem Oberseminar, Projektseminar …)) werden zu Beginn der Vorlesungszeit von der Betreuerin/dem Betreuer festgelegt. Die Arbeitsbelastung sollte der einer vierstündigen Vorlesung mit Übungen entsprechen.

Die Betreuerin/der Betreuer entscheidet am Ende der Vorlesungszeit, ob die Studienleistung bestanden ist oder nicht. Im Vertiefungsmodul gibt es eine mündliche Abschlussprüfung über den Stoff des Lesekurses und den weiteren Stoff des Moduls.____________________________________________

Typisches Semester:  

9. Fachsemester, unmittelbar vor der Master-Arbeit

Kommentar:  

Teil des Vertiefungsmoduls im Master-Studiengang ; kann auch für das Modul „Mathematik“ oder das Wahlmodul verwendet werden.

Notwendige Vorkenntnisse:  

hängen vom einzelnen Lesekurs ab

Studienleistung:  

wird vom Betreuer festgelegt

Prüfungsleistung:  

Das Vertiefungsmodul wird mit einer mündlichen Prüfung über u.a. den Stoff des Lesekurses abgeschlossen.

 
PIC    
Abteilung für
Angewandte Mathematik
SS2016 PIC_________________________________________________________

Projektseminar:  

Numerik

  

Dozent:  

Prof. Dr. D. Kröner

  

Zeit/Ort:  

Mi 14–16 Uhr, SR 226, Hermann-Herder-Str. 10

  

Tutorium:  

N. N.

  

Web-Seite:  

http://aam.uni-freiburg.de/

  
 
_______________________________________________________________

Inhalt:

In diesem Projektseminar werden Bachelor- und MasterstudentInnen sowie auch DoktorandInnen über die Zwischen- bzw. Endergebnisse ihrer Arbeiten berichten._________________________________

Typisches Semester:  

ab 6. Semester

Notwendige Vorkenntnisse:  

nach Absprache

Sprechstunde Dozent:  

Mi 11–12 Uhr und n.V., Zi. 215, Hermann-Herder-Str. 10

 

Abteilung für
Reine Mathematik
SS2016 PIC_________________________________________________________

Forschungseminar:  

Internationales Forschungsseminar
Algebraische Geometrie

  

Dozent:  

Prof. Dr. Stefan Kebekus

  

Zeit/Ort:  

zwei Termine pro Semester, n.V., IRMA – Strasbourg,
siehe Website

  

Web-Seite:  

http://home.mathematik.uni-freiburg.de/kebekus/ACG/

  
 
_______________________________________________________________

Inhalt:
The Joint Seminar is a research seminar in complex and algebraic geometry, organized by the research groups in Freiburg, Nancy and Strasbourg. The seminar meets roughly twice per semester in Strasbourg, for a full day. There are about four talks per meeting, both by invited guests and by speakers from the organizing universities. We aim to leave ample room for discussions and for a friendly chat.

The talks are open for everyone. Contact one of the organizers if you are interested in attending the meeting. We have some (very limited) funds that might help to support travel for some junior participants.____________________________________________________________________________________________

Typisches Semester:  

Endphase des Haupt- oder Masterstudiums

Sprechstunde Dozent:  

n.V., Zi. 432, Eckerstr. 1

 

Mathematisches Institut

SS2016 PIC_________________________________________________________

Veranstaltung:  

Kolloquium der Mathematik

  

Dozent:  

Alle Dozenten der Mathematik

  

Zeit/Ort:  

Do 17 :00 Uhr, HS II, Albertstr. 23 b

  
 
_______________________________________________________________

Inhalt:
Das Mathematische Kolloquium ist eine gemeinsame wissenschaftliche Veranstaltung des gesamten Mathematischen Instituts. Sie steht allen Interessierten offen und richtet sich neben den Mitgliedern und Mitarbeitern des Instituts auch an die Studierenden.

Das Kolloquium wird im Wochenprogramm angekündigt und findet in der Regel am Donnerstag um 17 :00 Uhr im Hörsaal II in der Albertstr. 23 b statt.

Vorher gibt es um 16 :30 Uhr im Sozialraum 331 in der Eckerstraße 1 den wöchentlichen Institutstee, zu dem der vortragende Gast und alle Besucher eingeladen sind.

Weitere Informationen unter http://home.mathematik.uni-freiburg.de/kolloquium/

 

 

 

Impressum
Herausgeber:
Mathematisches Institut
Eckerstr. 1
79104 Freiburg
Tel.: 0761-203-5534
E-Mail: institut@math.uni-freiburg.de

[prev] [prev-tail] [front] [up]