3.2 Elementargeometrie

Inhalt:

Elementargeometrie ist jedem von uns in der Schule begegnet, zum Beispiel in Gestalt von Sätzen über Drei- und Vierecke in der Euklidischen Ebene. In diesem Proseminar wollen wir die Grundlagen der Euklidischen Geometrie besser verstehen, und andere Geometrien kennenlernen. Dabei werden wir sowohl den axiomatischen Zugang als auch konkrete Modelle wie den 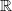² behandeln. Insgesamt geht es mehr um einen Überblick über verschiedene Arten, Geometrie zu betreiben, als um vertiefte Kenntnisse in einem speziellen Gebiet.

Im ersten Teil des Proseminars beschäftigen wir uns mit Axiomen, die nur über Punkte, Geraden und die Enthaltenseinsrelation sprechen (Inzidenzgeometrie). Je nach Wahl der Axiome erhalten wir zum Beispiel die projektive und die affine Geometrie. In diesen beiden Geometrien lassen sich Koordinaten einführen, wodurch man ihre Modelle algebraisch behandeln kann. Nimmt man die Sätze von Desargue bzw. Pappos-Pascal als Axiome mit hinzu, so erhält man Geometrien über Schiefkörpern bzw. Körpern.

Im zweiten Teil führen wir Anordnungs-, Kongruenz- und Vollständigkeitsaxiome ein. Jetzt können wir von gleich großen Strecken und Winkeln und von Isometrien sprechen. Neben der euklidischen Geometrie lernen wir Modelle der hyperbolischen Geometrie kennen, in der nur das Parallelenaxiom verletzt ist. Außerdem können wir auch auf der Kugel Abstände und Winkel messen und erhalten so die sphärische Geometrie. In diesen drei Geometrien gelten Dreieckssätze wie z.B. Sinus- und Cosinussatz, die aber in jeder der Geometrien eine andere Gestalt haben.

Im letzten Abschnitt wollen wir neben Längen und Winkeln auch Flächen von Polygonen und Volumina von Polyedern in der Euklidischen, sphärischen und hyperbolischen Geometrie messen. Wir werden sehen, dass zwei ebene Polygone genau dann den gleichen Flächeninhalt haben, wenn sie sich in kongruente Teilpolygone zerlegen lassen. Im dreidimensionalen Raum gilt das nicht mehr.

Literatur:

1. Wird in der Vorbesprechung bekanntgegeben.